Hogyan használjuk a matematikai mintákat a weboldal tervezésében, designonstop - a tervezésről
Évszázadokon át a matematikát a művészetben és az építészetben is használják. De a matematikát ritkán használják a weboldalak tervezésében. Valószínűleg, mert közös álláspont van, hogy a matematika és a kreativitás összeegyeztethetetlen dolgok. Bár ez a vélemény megdönthető, a matematika jó eszköz a weboldalak létrehozásához. Ebben az esetben azonban nem szabad kizárólag a matematikára támaszkodni. Valami másra van szükség itt.
1. Arany rész vagy arany téglalap
Az arany szekció (az arany arány, az extrém és a középső arány szerinti osztás) a folyamatos mennyiség két részre való felosztása oly módon, hogy a kisebb rész így a nagyobbra, egészre kiterjedő egészre utal. A részek arányát ebben az arányban egy irracionális matematikai konstanssal fejeztük ki, amely körülbelül 1,618033987-nek felel meg.
Általánosan elfogadott, hogy az "arany szekciót" tartalmazó tárgyakat az emberek leginkább harmonikusnak tartják. Itt érdekes tény a Wikipedia-ból. Ismeretes, hogy Szergej Eisenstein az "aranyszelvény" szabályai szerint mesterségesen építette a "Potemkin csatahajó" filmet. A szalagot öt részre tört ki.
Az első három évben az akció a hajón zajlik. Az elmúlt két évben - Odesszában, ahol felkelés történt. Ez a városra való átmenet pontosan az arany szakasz pontján történik. És minden részében törés történik, az aranyszelvény törvénye szerint.
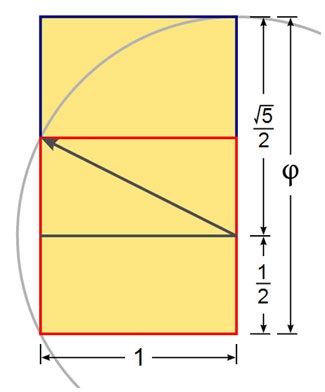
Most menj az Arany téglalapra. Minden egyszerű. Ilyen négyszögben a szomszédos oldalak hossza az arany szekció szabálya szerint korrelál, azaz 1: 1,618.
Annak érdekében, hogy egy arany téglalap alakuljon ki, először rajzoljon egy négyzetet (piros szín a képen), majd rajzoljon egy vonalat a négyzet egyik oldalának közepétől az ellenkező sarokhoz (vonal a kép nyilával). Ezt a vonalat használjuk körívként, amely meghatározza a téglalap magasságát. Most rajzolunk egy téglalapot (kék a képen).
Vegyünk szemléltető példaként ezt a minimalista tervezést, amelyet alább mutatunk be. 6 arany téglalapból áll, 299x185 képpont méretű, 3 téglalap alakú egy sorban. Ezeknek a négyszögeknek az oldalai a 299/185 = 1,616 aranyszelvény szerint korreláltak.
Jegyezd fel az arany téglalap körül nagy mennyiségű helyet. Olyan nyugodt és kellemes légkört teremt, amelyben a navigáció elemei szabadon lélegezhetnek. Annak ellenére, hogy csak néhány színt és azonos típusú blokkot használnak, az összes navigációs elem intuitíve érthető és szolgálja a céljukat.

Annak érdekében, hogy új blokkot adjon hozzá a terv logikájának megsértése nélkül, a legjobb, ha blokkokat ad hozzá a harmadik sorhoz, és hasonló módon lefelé mozog.

Alkalmazási területek. A Golden Rectangles használata a designban jól használható különböző fotóalbumokhoz, portfólió oldalakhoz és a termék bemutatására összpontosító webhelyekhez.
2. Fibonacci számok a tervezésben
A Fibonacci számok a számok matematikai sorozata. A definíció szerint az első két Fibonacci-szám 0 és 1. Minden egymást követő szám megegyezik a két előző összegével. Számos szám a következő: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...
A zenekarban a Fibonacci-számokat a hangszerek testreszabására használják, az építészetben a harmonikus arányok kiszámításához, például a szoba magasságának és a falak díszítésének magasságához különböző anyagokkal való arányát. A növény szárán lévő levelek (vagy ágak) közötti távolság nagyjából megegyezik a Fibonacci-számokkal.
A tervezés során a Fibonacci-számok fő alkalmazási területe a fő tartalommal (konténerek) és az oldalpanel méretének meghatározása. A módszer lényege a következő. Vegye ki a tartály alapszélességét, például 90 képpontot, és következetesen szorozzon a Fibonacci-sorozat számával. E számítások alapján a webhelyrács épül. Nézzünk egy példát.
Az oldal három oszlopra oszlik. A tartály alapszélessége 90 képpont. Ezután az első oszlop 180 képpontos (90 x 2) szélességű, a második oszlop szélessége 270 képpont (90 x 3) és a harmadik oszlop szélessége 720 képpont (90 x 8). A betűméret szintén összhangban van a Fibonacci-sorozattal. A fejlécben lévő betűméret 55 képpont, a betűméret 34 képpontos, a szöveg betűmérete pedig 21 képpont.
Ha a webhely fix szélességű, például 1000 képpont, akkor a Fibonacci-számok nem nagyon kényelmesek. Amennyiben a Fibonacci-sorozathoz legközelebb eső 1000-es szám 987 (..., 610, 987, 1597 ...), akkor ebből a számból ki kell számolnunk a helyszínblokkok szélességét. Ilyen helyzetekben a legjobb, ha az Aranyszekció szabályát használjuk (1000 x 0.618 = 618px), és a blokkok szélességének meghatározásához továbblépjük.
Alkalmazási területek. A Fibonacci-számok leginkább a blogok és a magazin elrendezések tervezéséhez alkalmazhatók.
3. Öt elem vagy Kundli design
Egy másik érdekes példa a tervezés matematikájára egy olyan módszer, amely a Kundli indiai horoszkóp összeállítására épül. Itt az alap a következő ábra. Egy négyzetet rajzolunk, két átlós vonalba rajzolunk, összekötve az ellentétes sarkokat, majd a szomszédos oldalak középpontjai vonalakkal vannak összekötve.
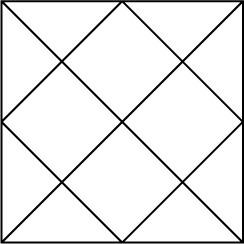
A téren négy rombusz látható. Ez az alap az elrendezés öt elemének kialakításához az oldalon.
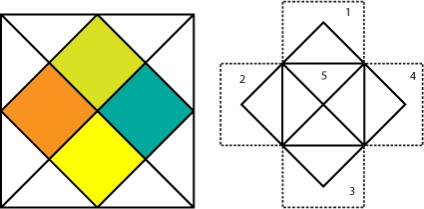
A következő példa a helymeghatározás alapja a Kundli geometria. Ez az elrendezés alkalmas lehet egy egyoldalas névjegykártya-webhelyre, amely a jQuery technológián alapuló interaktív elemeket tartalmaz.
Ez az elrendezés könnyen átalakítható egy három oszlopos elrendezésű fejléccel és lábléccel rendelkező webhelyekkel.
Alkalmazási területek. Ez a design a legmegfelelőbb a portfólió-helyek és a termékek bemutatását célzó webhelyek számára.
4. Szinuszhullámok
Ha sokszínűséget szeretne, akkor nem kell betartania az arany szekció és a Fibonacci-szám alapszabályait. Kísérletezhet más jól ismert képletekkel.
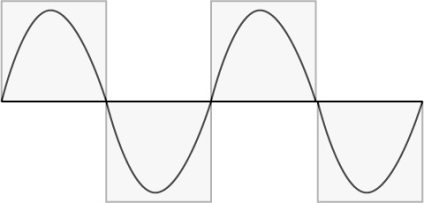
Lássuk, hogyan alakul ki az oldal elrendezése a szinuszos hullámok rezgései alapján matematikai függvénynek, amely ismételt oszcillációkat ír le. Az alábbi kép egy egyszerű és egyoldalas, egy oldalas weboldalra mutat példát.
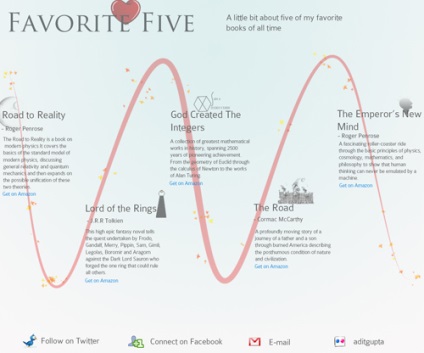
Vagy egy másik lehetőség. Egy fejlécből, öt oszlopból és láblémből álló elrendezés. Az ilyen oldalak is javíthatók a jQuery tippekkel, hogy interaktívabbá tegyék.
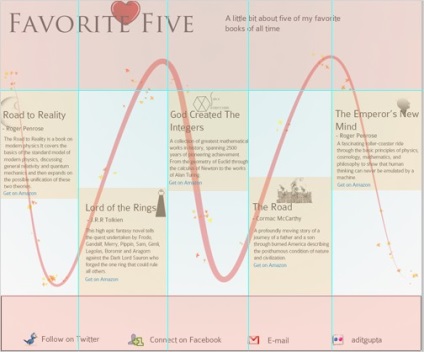
Alkalmazási területek. Ez a design olyan helyek számára optimális, ahol az események időrendjét tükrözni szeretné. A legalkalmasabb a vízszintes navigációhoz.
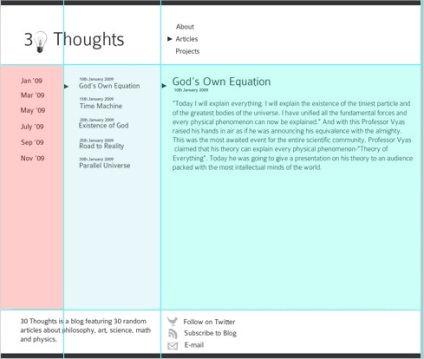
5. Harmadik szabályok
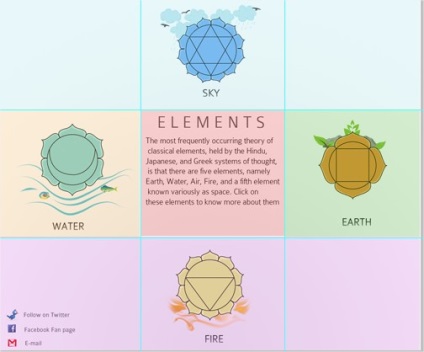
Ez a szabály kimondja, hogy a képet két vízszintes és két függőleges vonalra kell osztani 9 egyenlő részre. És minden fontos kompozíciós elemnek ezen a vonalon vagy a metszéspontjain kell elhelyezkednie.
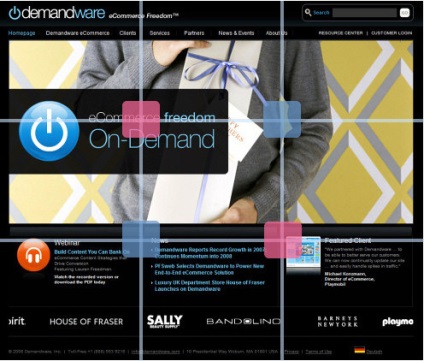
Ebben a példában a négy metszéspont közül kettő gyűjti össze a legfontosabb információkat. Jelölt rózsaszín négyzetekkel. És a navigációs blokk a második vízszintes vonal mentén helyezkedik el.