Egyenes hajlítás
BIOLÓGIAI INFORMATIKAI ÉS RÁDIÓ ELEKTRONIKUS EGYETEM
Műszaki grafika tanszék
"Egyenes vonalú rúd hajlítása"
A hajlítási deformáció általános koncepciói
A hajlítást (1. ábra, a) a rúd hosszirányú tengelyére merőleges külső erők okozzák, valamint olyan külső erők párosait, amelyeknek a cselekvési sík átmegy ezen a tengelyen. A terhelés hatására a rúd hosszirányú tengelye meghajlik. A rúd keresztmetszeteiben a hajlítás során a belső erők pillanatai merülnek fel, amelyeknek a síkja merőleges a szakasz síkjára, azaz hajlító pillanatok Mie.
Ha a keresztszelvényben a hajlítónyomaték a belső erők egyetlen komponense, akkor a kanyart tisztanak nevezzük.
A hajlítást keresztirányúnak nevezik, ha keresztirányú erők Q keresztmetszetűek a Mi hajlítónyomatékkal együtt. A keresztirányú hajlítás gyakoribb tényleges terhelési körülmények között fordul elő, mint a tiszta hajlítás.
Ha a Mi hajlító pillanat hatásmechanizmusa áthalad a keresztmetszet tömegközéppontján, azaz a szelvény bármely központi tengelyén keresztül a kanyart egyszerű vagy laposnak nevezik. ellenkező esetben a hajlítás ferde. Lapos hajlítással a rúd hosszanti tengelye deformálódik a külső erők síkjában, azaz egy lapos ívelt vonal. A ferde hajlítás esetén a deformáció síkja nem esik egybe a külső erők síkjával. A ferde hajlítás a deformáció alakjára utal, amelyet komplex deformációnak neveznek. Hajlított rudak támasztási reakcióinak meghatározása
A hajlított rudak keresztmetszeteiben a belső erőket keresztmetszeti módszerrel határoztuk meg. Az egyensúlyi egyenletek használata lehetséges a szabad testekre ható erőknek. A hajlító deformációnak valós körülmények között megfigyelt rudakhoz szükség van néhány vagy más támaszra, amelyek hiányában lehetetlen a rúd hajlítása. A hordozók (kötések) jelenléte korlátozza a hajlított rúd mozgását, és lehetetlenné teszi az egyensúlyi egyenletek használatát a belső erők meghatározásához.
Formálisan a nem-szabad hajlítópálcák a kötéskibocsátás elve alapján szabadnak tekinthetők. Elmondása szerint minden nem szabad testet szabadon lehet ábrázolni, elvetve a korlátokat (támogatja), korlátozva ezzel, és helyettesítve cselekvését az ilyen kötések reakcióerőivel. Az egyensúlyi egyenleteket használhatjuk a hajlított rudak keresztmetszetén belüli belső erők meghatározására is, feltéve, hogy a külső erőkön kívül a támaszok reakcióerői is figyelembe lesznek. Ezért, mielőtt meghatározná a hajlított rudak keresztmetszetében a belső erőket, meg kell tudnia találni a támasztékok reakcióinak nagyságát és irányát. Ismeretes, hogy a kapcsolat (támasz) reakciója mindig olyan irányba irányul, ahol a csatlakozás nem teszi lehetővé a test mozgását. Ha a kommunikáció megakadályozza a test transzlációs mozgását, akkor a reakció ereje; ha a kapcsolat megakadályozza a forgási mozgást, akkor a reakció az erők pillanatát jelenti.
A hajlításnak három fő típusa van.
A mozgatható csuklós tartó (2. ábra, a) nem akadályozza meg a rúd forgását és mozgását a tartófelületen. A tartó reakciója a csukló közepén halad át, és merőleges a referenciasíkra.
Az álló, csuklós tartó (2, b ábra) lehetővé teszi a rúd elfordulását, és megakadályozza annak bármilyen irányban történő transzlációs mozgását. A reakció áthalad a csuklópánton, és a külső erők rendszerének működésétől függően eltérő irányban lehet. A külső erőknek a rúd hosszirányú tengelyére merőleges és merőleges síkjában lévő komponensekké bomlik.
A merev beágyazás vagy csípés (2., c ábra) nem teszi lehetővé a hajlított rúd lineáris vagy szögletes elmozdulását. Teljes mértékben támogatja a reakció erő tagja, amelyek elbomlanak két komponensre mentén irányul, és merőleges a hosszanti tengelye a rúd és a forgatónyomaték (reaktív nyomaték), amely a reakció támogatást kapcsolódnak egy olyan ponton becsípõdésének rúd. A rúd, amelyet egyik vége megcsíp és nincs más támaszai, az úgynevezett konzol. A konzolt a rúd azon részének is nevezik, amely a csuklópántokon túlnyúlik.
Továbbá, a "támasztékok" helyettesítésével a reakciók erőivel a kiegyensúlyozott rúdra ható erők rendszerének egyensúlyi egyenleteit alkotják. Független egyensúlyi egyenletek egy síkerő-rendszer esetén három. A probléma statikusan meghatározható, ha a támogató reakciók ismeretlen összetevőinek száma nem több mint három.
Ez a következő lehetőségekkel lehetséges a hajlított rudak rögzítéséhez: a rúd egyik végével (érintkező rugó), vagy a rúd rögzítéséhez mozgatható és rögzített csuklópántok (tengelyek) segítségével. A reakciók több ismeretlen összetevőjével a megoldás egyéb módszerei nem szerepelnek a kézikönyvben.
Ha a támasz reakciójának nagysága negatív a számítás során. mínusz jellel, akkor a reakció tényleges iránya ellentétes a feltételezettel. amelyet figyelembe kell venni a belső erők meghatározásakor.
Meghatározzuk a reakciókat a hajlított rúd A és B támaszain, a rakodási sémán (F, Me) és a méretek (a, b, # 8467;), amelyek az 1. ábrán láthatóak. 1, a. A B mobiltartót a RB reakcióval helyettesítjük. és az A rögzített csuklópántot - a RAX és a RAY komponenseket. A "szabad" rúd a támaszok külső erőinek és reakcióerőinek hatása alatt nyugalomban van. A sík mozgásának lehetséges komponenseinek hiánya (az x és y tengely mentén történő transzlációs mozgás és az erők cselekvési síkjában lévő forgó mozgás, vagyis a z tengely körül), az egyensúlyi egyenletek segítségével fejezzük ki:
Az erők működtető rendszere esetében az első egyenlet (1) RAX = 0 formában van; második: RB - F - RAY = 0 és a harmadik: RB # 8467; - F # 903; a - Me = 0. Az utolsó egyenletből meghatározzuk, hogy RB = (F # 903; a + Me) / # 8467; Ezután helyezzük el az RB értékét a második egyenletben, meghatározzuk, hogy RAY = F - RB = F - (F # 903; a + Me) / # 8467;
A belső erők meghatározása a hajlítás során. Keresztirányú erők és hajlítónyomaték ábrázolása
A sík keresztirányú hajlítás esetén a belső erők következő összetevői jelennek meg a rúd keresztmetszetében: a Q keresztirányú erő és a hajlítónyomaték Mi. Ezek meghatározásához használja a szakaszmódszert.
A keresztirányú erő a szakasz síkja mentén van irányítva, és a hatása a nyírófeszültség hatásához kapcsolódik, azaz # 964; = f (Q). A rúd bármelyik keresztmetszetében a keresztirányú erő számszerűen megegyezik a vetületek algebrai összegével az összes külső erők szakaszának síkjával és a támaszok reakciójával a szakasz egyik oldalán. A szakaszban pozitívnak tekinthető (3. ábra a), ha a szakasz bal oldalán fellépő erők következménye felfelé irányul, vagy a szelvény jobb oldalán fellépő erők lefelé vannak; és negatív (3. ábra, b) - az eredmény ellentétes irányával.
A hajlítónyomaték a keresztmetszettel merőleges síkban hat. A hatása a normál feszültségek hatásával jár együtt, azaz # 963; = f (MI). A hajlító nyomatékot bármely keresztmetszete a rúd számszerűen egyenlő a algebrai összege pillanatok a tömegközéppontja a keresztmetszet külső erők és a reakciók támogatja ható egyik oldalán a szakasz. A hajlító nyomatékot pozitívnak tekintjük, ha a rúd keresztmetszete (3C.) Meg van hajlítva lefelé domború, és a negatív (ábra. 3, g) ha a rúd van hajlítva, a keresztmetszet dudor felfelé. A hajlítónyomaték jele a szekcióban a feltételes keresztmetszet rögzítésével és a két oldalán található erők hatásának figyelembevételével határozható meg. Pl. 1, a. az 1-1. szakasz bal oldalán és a 2-2. szakasz jobb oldalán hatva mozog a rúd ezen szakaszaiban konvexitással lefelé, azaz. Mi 1-1> 0 és Mi 2-2> 0.
A Q és a Mi meghatározásakor egy csúszó koordinátarendszert használnak, amikor a keresztmetszet a bal szélső keresztmetszet vagy a rúd jobb szélső keresztmetszete alapján számít.
A konzol mereven rögzítve az egyik oldalon (ábra. 5,24, a) egy keresztirányú erő rudak és a hajlítónyomaték megállapítása nélkül kényelmes, hogy meghatározza a támogatási reakciókat, figyelembe véve, tekintettel a keresztmetszete a ható erők a laza részét a rúd. A Q és MI értékei a B rögzítési pontban megegyeznek a hordozóreakció komponenseivel, azaz QB = F = RBY. MiB = F # 903; # 8467; = MRB.
A Q keresztirányú erő és a Mi hajlítónyomaték általában a keresztmetszet helyzetétől függ a rúd hosszától, azaz a rúd hosszától. az x értéke. Az erőviszonyok ellenőrzését a legveszélyesebb szakaszokban végezzük, a legnagyobb belső erőkkel és maximális feszültségekkel rendelkező szakaszokban. Ahhoz, hogy megtalálja a veszélyes szakaszok és a képi ábrázolása a karakter változások a belső erők ábrázolja a eloszlása a keresztirányú erőket Q = Q (x) és a hajlító nyomaték Mi = Mi (x) hossza mentén a rúd, azaz keresztirányú erők és hajlítónyomaték ábrái.
A rúd szakaszokra van osztva, amelyek alatt a terhelés egyenletes. A Q és Mi diagramok esetében a rúd hosszanti tengelyével párhuzamos vonalakat húzzák. A vonalak határait lebontják ezen a vonalon. Az egyes szakaszok esetében a Q = Q (x) keresztirányú erő és a hajlítónyomaték közös kifejezései a Mg = MI (x) alakúak, melynek tetszőleges részei a diagramon belül vannak. Ezután elkészülnek a Q és MI diagramok. az x argumentumot az egyes szakaszokon belüli értékekre állítja be. A keresztirányú erő és a hajlítónyomaték értékeit ábrázolják a cselekmény ordinátáinak egy skálán: Vegyük figyelembe a változást # 964; négyszögletes keresztmetszetű rúdhoz (5.23. ábra, b). Az árnyékolt terület statikus pillanata a semleges z tengelyhez viszonyítva egyenlő
- a z tengelytől a vágási szakasz tömegközéig. Ez a parabola egyenlet. A tangenciális feszültségeket a képlet határozza meg, figyelembe véve, hogy Iz = bh 3/12;
.
A keresztmetszet legnagyobb tangenciális feszültsége a semleges tengely szintjén hat. A téglalap alakú keresztmetszetű rudak esetében 1,5-szer nagyobbak azok a feszültségek, amelyek a keresztmetszet mentén egyenletes eloszlású tangenciális feszültségekkel rendelkeznek.
A hajlítás tangenciális feszültsége a semleges tengelyen és a keresztmetszet egyéb formáival maximális. A kerek keresztmetszetű rudak egyenlőek # 964; max = (4/3) (Q / A), a gyűrűszakasz rúdjaihoz - # 964; max = 2 (Q / A).
A tangenciális feszültségek mentén hajlító rudak szilárdságának feltétele # 964; max ≤ # 964; ahol # 964; adm - a rúd anyag megengedett feszültsége nyírásra vagy nyírásra. Megjegyezzük, hogy a nyírási feszültségek keresztmetszetének hajlított rúd sokkal kisebbek, mint a normál, így a számítás az erő általában a normál feszültséget összhangban expressziós hatása nélkül az oldalirányú erők.
Hajlítási törzsek meghatározása
Ha a hajlítás, törzs a rúd keresztmetszete (4a.) Határozza meg mozog a tömegközéppontja a keresztmetszet merőleges az eredeti helyzetébe a rúd tengelyével, az úgynevezett eltérítési elfordulási szög és # 952; szakaszát az eredeti helyzetéhez képest. Ahhoz, hogy megtaláljuk a deformációkat a rúd hosszában a keresztmetszetekben, meg kell szerezni az y = y (x) és # 952; = # 952; (x). Az elsőt egy görbült tengely vagy egy eltérési egyenlet egyenletének nevezik.
A rúd görbült tengelyének érintője bármelyik pontján az eredeti tengellyel megegyezik a forgásszögnek megfelelő szöggel # 952; egy adott ponton. Tangens szög # 952; az érintő tg # 952 meredeksége; = dy / dx. Mivel azonban a tényleges értékeit forgásszögeinek keresztmetszetek hajlítás közben kicsi, nagyságrendileg ezred radián, lehetséges, hogy egyenlőségjelet tesznek az érintő szög értéke (tg # 952; ≈ # 952;), és keresse meg a szelvény forgási szöge és a függőleges alakváltozás közötti kapcsolatot # 952; ≈ ≈ dy / dx.
A matematika tanfolyamából az alábbi összefüggés ismeretes az x0y síkban lévő vonal K görbületén:
De mivel (dy / dx) 2 = tg 2 # 952; = # 952; 2 <<1, то выражение (2) упростим, представив в виде
A függőség használatával (5.67) a rúd tengelyének görbületét összekötjük a Mi hajlító pillanattal és az EIz keresztmetszet merevségével:
A kapott (3) és (4) függőleges görbület-kifejezések összehasonlításával megkapjuk a rúd ívelt tengelyének differenciálegyenletét:
amelynek beillesztése nem nehéz. A kifejezés kijelölését az elfogadott koordináta-rendszer határozza meg.
Az M hajlítónyomaték korábban elfogadott jele (4., b, c, d, q ábra) nem függ a koordináta tengelyek irányától.
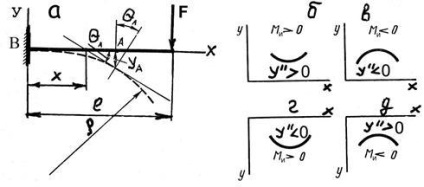
A vonal görbülete pozitív, pl. y '' = d 2 y / dx 2> 0, ha a konkáv görbe egybeesik a pozitív iránya az y tengelyen (4B., d) vagy fordítva (ábra. 4c, d).
Ha az y tengely felfelé van felvéve, az egyenlet (5) jobb és bal oldalának jelei mindig ugyanazok, mint pl. az y ''> 0 és a Mi> 0, valamint az y '' <0 и Ми <0. Поэтому выражение 5) представим как
A rúdszakaszok deformációit vagy szög- és lineáris elmozdulásait meghatározó egyenletek megtalálásához szükség van az egyenlet integrálására. Ha egyszer az egyenletet integráljuk, akkor kapjuk a forgási szög egyenletét
Az egyenlet integrálását (5.80) második alkalommal megkapjuk az eltérések egyenletét
ahol C és D az integráció konstansjai, amelyeket a határfeltételek határoztak meg, amelyek a hajlított rudak rögzítésének feltételei.
Így az egyik végén mereven rögzített rúd esetében az y elhajlásnak és a szelvény forgásszögének a rögzítési ponton nullanak kell lennie. A csuklós támaszokra támaszkodó rúdhoz az elhajlás nulla a rögzítési pontokon.
Határozza meg a rúd konzol szabad végének elhajlását és forgási szögeit (4. # 8467;. amelyet a végén egy koncentrált erő F. A rúd merevsége állandó hosszúságú és egyenlő az EI-vel.
A koordináták eredete a rúd merev rögzítésének B pontjában történik. Az y tengely felfelé irányul, az x tengely jobbra van irányítva.
Tetszőleges keresztmetszetben, amely az eredetétől számított x távolsággal van elválasztva, a hajlítónyomaték M, = -F (# 8467; -x). A hajlított tengely differenciálegyenletét EI (d 2 y / dx 2) = -F (# 8467; -x) formában kapjuk. Integrálása ezt az egyenletet kapjuk, hogy EI (dy / dx) = = -F × [# 8467; x - (x 2/2)] + C további integrálása, megkapjuk egyenletet alakváltozása
EIy = -F [(# 8467; x2 / 2) - (x3 / 6)] + Cx + D.
Figyelembe véve, hogy az x = 0 rögzítési pontján az y eltérés és a szakasz forgási szöge # 952; = dy / dx egyenlő nullával, azt találjuk, hogy az integrációs állandók C = 0 és D = 0. Akkor a szabad végnél a rúd x = # 8467; y = (-F # 8467; 3) / (3EI) eltérés és a végszakasz elfordulási szöge # 952; = dy / dx = (-F # 8467; 2) / (2EI).
Az eltérítésre és a forgásszögre vonatkozó kifejezések mínusz jele azt jelzi, hogy az eltérés az y tengely pozitív irányával ellentétes irányban van. azaz lefelé, és a végszakaszt az óramutató járásával megegyező irányba forgatják.