Az aszimmetrikus terhelésű áramkör kiszámítása

Légvezeték> A szimmetrikus összetevők módszere

Normál körülmények között a nagyfeszültségű háromfázisú áramkörök aszimmetrikus rendszerei viszonylag ritkák (főleg elektromos ívű kemencék és egyfázisú elektromos vontatómotorok láncolataiban). Általában az aszimmetrikus üzemmódok vészhelyzeti körülmények között érkeznek, amikor az aszimmetria bármely láncban megjelenik.
Az aszimmetria két típusa van - keresztirányú és hosszanti. A szimmetrikus háromfázisú áramkör keresztirányú aszimmetriája aszimmetrikus terheléssel jár. Ide tartoznak különösen az aszimmetrikus rövidzárlatok (a fázisok közötti lezárások, az egy vagy két fázis lezárása a talajra). Hosszanti aszimmetria keletkezik, ha az elemek egyenlőtlen ellenállásokkal, vagy egy vagy két vezeték megszakadása esetén (egy vonal kiegyensúlyozatlan része) szerepelnek a fázisvonal vágásban.
Számítások aszimmetrikus módok háromfázisú áramkör, amely használja az elv a kártérítés, a vevő helyett aszimmetrikus vagy kiegyensúlyozatlan részét a forrás hálózati feszültség (feszültség), mely értékek kiszámításához a teljes lezárás továbbra is ismeretlenek. Ennek a módszernek a célszerűsége, hogy az ilyen csere után az áramkör szimmetrikusvá válik, és az áramok és feszültségek ellentétes szimmetrikus összetevői nem függenek egymástól. Az áramok szimmetrikus alkatrészeinek és a különböző szekvenciák feszültségének az aszimmetria által okozott kapcsolatait később vezetik be.

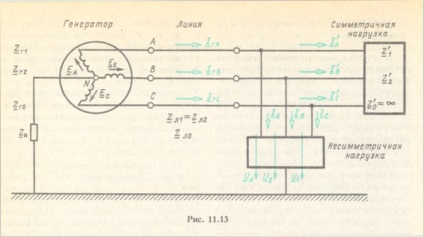
Tekintsük a számítási módszert a 2. ábrán látható áramkör példáján. 11.13, amely szimmetrikus dinamikus () és aszimmetrikus statikus terheléseket tartalmaz. Hagyja a generátorok emf és az áramköri elemek ellenállását megadni. Meg kell találni áramokat és feszültségeket. Az 1. ábrán. 11.13 az áramkör és a kiegyensúlyozatlan terhelési ellenállás nincsenek feltüntetve, mivel ezek nem szükségesek a számítás első szakaszában.
Az aszimmetrikus terhelést három, nem ismert feszültségű EMF forrással helyettesítjük, és szimmetrikus áramkört kapunk, amely a szimmetrikus EMF-rendszerrel rendelkező generátor mellett aszimmetrikus feszültségű forrásokat is tartalmaz.

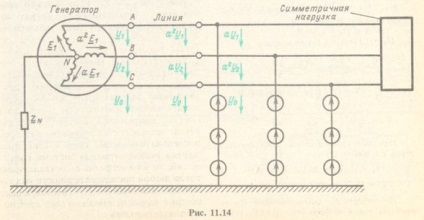
A feszültségeket szimmetrikus komponensekké bontjuk. az A fázist a fõre. Ennek eredményeképpen egy szimmetrikus sémát kapunk (11.14. Ábra), és az aszimmetrikus terhelésű ágban három közvetlen, fordított és nulla szekvencia szimmetrikus rendszere van.

Egy szimmetrikus áramkörben bármely szekvencia szimmetrikus rendszere szimmetrikus áramlási rendszert eredményez, amely azonos szekvenciájú. Következésképpen három független rendszert tudunk összeállítani, amelyek a 3. ábrán láthatóak. 11.15, a-c. Az egyszerűség kedvéért ezek a rendszerek nem veszik figyelembe a vonal részleges kapacitását (lásd a szakaszt).
Az eredeti áramkör A fázisának módját (lásd a 11.13. Ábrát) úgy határozták meg, hogy a három áramkör módjait egymásra helyezték.
Az előre- és hátrafelé irányuló szekvenciák konfigurációi mindig ugyanazok. A nulla-sorrendű áramkör általában nagyon különböző. Ebben a példában nincs elágazás, mivel a háromfázisú áramkör jobb oldali részén nem lehet zérus sorrendű áramerősség (lásd a 11.13. Ábrát). Különös figyelmet kell szentelni annak a ténynek, hogy a semleges vezetékben lévő ellenállást hármas értéken vezetik be a nulla sorrendű áramkörbe (lásd a fejezetet).
Figyelmen Mapping azt mutatja, hogy a legmagasabb értékeket a szimmetrikus komponenseinek feszültségek negatív és zérus sorrendű helyén megfigyeltünk egy aszimmetrikus kapcsolatot a vevő, mint a reakcióvázlatokon nevezetesen vannak források EMF negatív és zérus sorrendű.
További számításokhoz célszerű az egyes szekvenciák sémáit a legegyszerűbb formává alakítani anélkül, hogy az ágakat ismeretlen feszültségek forrásával befolyásolnánk.

A közvetlen szekvencia-áramkörben a generátor és a szimmetrikus vevők ágait egy egyenértékű generátorral helyettesítjük (11.16 ábra, a):

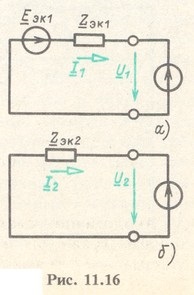
A fordított sorrendű sémában kombináljuk a generátor és a szimmetrikus vevő ágait (11.16, b ábra):

Ebben a példában a nulla szekvencia séma nem igényel konverziót, mivel a legegyszerűbb formában van.
Mindhárom séma esetében az egyenleteket a második Kirchhoff-törvény szerint írjuk:

Ennek a három egyenletnek hat ismeretlen volta van. A hat ismeretlen mennyiséget összekötő további három egyenlet összeállítható egy adott áramkör és egy aszimmetrikus vevő paraméterei alapján.
Ábra. 11.16

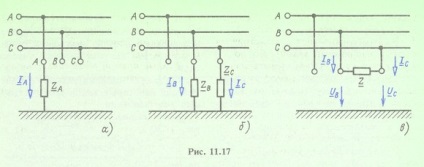
Tegyünk további egyenleteket bizonyos típusú aszimmetrikus vevők számára. A 2. ábrán látható vevőkészülékhez. 11.17, a

A 2. ábrán látható vevőkészülékhez. 11.17,6

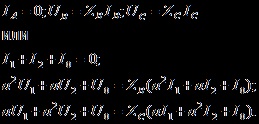
Ha az aszimmetrikus vevő nem kapcsolódik a földhöz, például a 2. ábrán látható áramkörhöz. 11.17, c, a nulla szekvencia áramok szimmetrikus összetevői nulla, és az előző számítási szakaszokban a nulla szekvencia áramkörének összetétele lemerül. Két alapvető egyenletet kapunk négy ismeretlenel, és csak két további egyenletet kell készíteni:

Hasonló módon további egyenleteket alakítanak ki más típusú statikus aszimmetrikus terheléshez. A Kirchhoff-féle egyenletek párhuzamos megoldásában további egyenletekkel rendelkező szekvenciák esetén az A fázis áramának szimmetrikus összetevőit egy ágban egy aszimmetrikus vevőhöz határozzuk meg. E komponensek eloszlását a közvetlen, a kölcsönös és a nulla szekvenciák sémáinak egyéni ágai határozzák meg. A jelenlegi összetevők ismerete minden ágban, számítsa ki a tényleges áramot az egyes fázisokban és a különböző szekvenciák feszültségcsepp komponenseit, majd az áramkör egyes szakaszaiban lévő fázisfeszültségeket.
Adjuk meg az áramkör rezsimjének kiszámítását (lásd a 11.13. Ábrát) az aszimmetrikus terhelés esetében, amely a 3. ábrán látható. 11.17, a feltéve, hogy (egyfázisú földi hiba). Készítsünk további egyenleteket

A (11.24) -től (11.23) levonva (11.24) megkapjuk

Ezt az eredményt (11.23) helyettesíti

Helyettük őket (11.21), majd hozzáadjuk őket, és figyelembe véve (11.22), megkapjuk

A feszültségek szimmetrikus összetevőit (a földzárlat helyén) a (11.21) pont határozza meg:

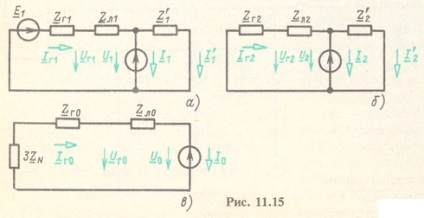
Az 1. ábrán látható áramkörök esetében 11.15, és

Ábra. 11.15, b

Ábra. 1115, ben

A generátor kapcsaihoz tartozó feszültségek szimmetrikus összetevői a 4. ábrán bemutatott sémákban találhatók. 11.15:

Kapcsolódó cikkek

előző ◈ a következő