Az 1985 - ös rémálmok entrópiája és valószínűsége 2006 - ban
Az entrópia és az állam valószínűsége
Ismeretes, hogy bármely rendszer kívülről történő befolyásolása nélkül olyan állapotba kerül, amely a lehető legkisebb potenciális energiával jellemezhető. Ez az információ lehetővé teszi, hogy bizonyos mértékig megjósolni az áramlási iránya egy folyamat in vivo „nélkül hatással van a testre, vagy a rendszer kívülről Ezen kívül, amint Clausius reálfolyamatok mindig fejleszteni oly módon, hogy az egyik legfontosabb jellemzője a rendszer állapota -. Entrópia - növekvő Következésképpen minden termodinamikai rendszer a potenciális energia és az entrópia maximuma irányába fog fejlődni, de nem csak a potenciális energia és entrópia segíthet meghatározni áramlási iránya a valós folyamatokat. Van egy másik, statisztikai, természeti törvény, amely kimondja, hogy a legvalószínűbb az állam a legnagyobb zavar.
Vegyünk egy olyan hajót, amely több összekapcsolt sejtből áll. Ez a hajó n molekulákat helyezzük el, amelyek szabadon mozoghatnak az edényen a sejtből a sejtbe, bármilyen módon elosztva. Ennek a disztribúciónak a jellege nagyon változatos lehet. Példaként tekintse meg a hat molekula eloszlását három sejtben. Az egyszerű érvek meggyõzõdnek arról, hogy a molekulák sejtekbe történõ eloszlatásának különbözõ módjai lehetségesek, amelyek közül néhányat a 9. ábrán mutatunk be. Példaként vegyük figyelembe ezt a helyzetet. A doboz három részre oszlik. Tegyük fel, hogy egyikük molekulákat tartalmaz; a másik kettő üres. A részecskék ilyen rendszere rendezettnek tekinthető. A rekeszek közötti partíciók eltávolítása során észrevesszük, hogy a kaotikus termikus mozgásban részt vevő molekulák egy idő múlva elfoglalják a számukra adott összes kötetet. Megfigyelése tovább, azt látjuk, hogy a molekulák újraelosztott úgy, hogy mindegyik rekesz tartalmaz körülbelül azonos számú molekulát, bár bizonyos eltérések elkerülhetetlenek, és - ingadozások, hogy lesz a kisebb, annál nagyobb a kezdeti molekulák száma egy dobozban. Így a magához hagyott rendszer a legvalószínűbb állapotba kerül: azonos számú molekula minden egyes rekeszben. Ez az újraelosztási folyamat olyan irányba fejlődik, amely után az entrópia növekszik; míg a rendszer a legvalószínűbb állapotba kerül. Ellenkező esetben az entrópia növekedése az állam valószínűségének növekedésével jár. Az állam valószínûségének mennyiségi jellemzõje a termodinamikai valószínûség, amely nem más, mint egy adott fizikai rendszer állapotának megvalósíthatósága. A 9. ábra szerinti eloszlás valószínűleg.
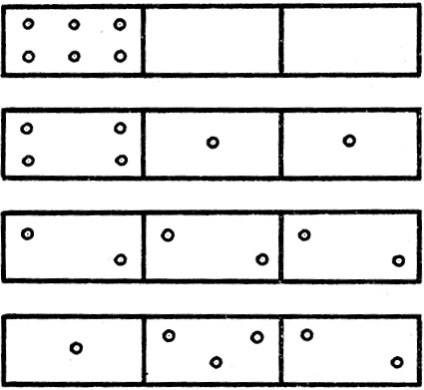
Ábra. 9. A molekulák eloszlási módjai a sejtekben
Termodinamikai folyamatok tanulmányozásakor Boltzmann általánosságban észlelt egy bizonyos rendszer entrópiájának változását és egy állam termodinamikai valószínűségének értékét. Megállapította, hogy egy adott termodinamikai rendszer entrópiája arányos az állapotának valószínűségének logaritmusával. Az entrópia növekedése a rendezés zavarát, a rendszer hajlamát a részecskék kaotikus mozgására utalja. A Boltzmann elméleti tanulmányai szerint
A Boltzmann elméleti tanulmányai (34)
ahol S a rendszer entrópiája; W az állapotának termodinamikai valószínűsége.
Boltzmann elképzeléseinek továbbfejlesztése az entrópia és az állam valószínűsége közötti kapcsolatról, a német fizikus M. Planck megállapította az arányossági együtthatót (34), és megkapta az egyenlőséget
Az arányossági együttható (35)
ahol k állandó, később Boltzmann konstansnak nevezik.
Boltzmann és Planck munkáiból következik, hogy a termodinamika második törvénye, mint az első, statisztikai törvény. A termodinamika második törvénye csak nagyszámú molekulára vonatkozik, amelyre statisztikai módszerek alkalmazhatók. Clausius növekvő entrópia törvényét átlag statisztikai következtetésként kell értelmezni. A rendszer egyes részeiben olyan folyamatok alakulhatnak ki, amelyek fejlődnek úgy, hogy a rendszer ezen része entrópiája csökkenhet, bár összességében a makroszöveget az entrópia növekedése jellemzi. Az energia, a sűrűség és a hőmérséklet ingadozása folyamatosan felmerül, és viszonylag rövid időn át eltűnik. A legvalószínűbb állapot azt jelenti, hogy a rendszer termodinamikai egyensúlyi állapotban van. Az entrópia és a termodinamikai valószínűség közötti kapcsolat lehetővé teszi számunkra, hogy megállapítsuk, hogy az entrópia egy elszigetelt rendszer közelségének mércéje a termodinamikai egyensúly állapotának.