A shaderek programozása a hlsl-en
Valószínűleg mindenki hallott a világítási modellekről, mindenütt körülvesz minket: pl. Minden tárgyat, ugyanazt az üvegt az asztalon állva. Bizonyos fény ráesik rá, pontosabban, a nap fényétől vagy bármely más megvilágítási forrásától, ezt egy bizonyos világítási modellnek nevezik. A gyakorlatban senki sem próbál programozni a fény minden fizikai elveit, mivel számításuk nagyon költséges. Mindazonáltal számos modellt találtak fel, amelyek reális eredményeket adnak a kis számításokhoz.
Nézzük még részletesebben, létrehozzunk egy egyszerű megvilágítási modellt - egyenletes megvilágítást.
1. Egységes világítás.
Az egységes világítás (környezeti megvilágítás) állandó kezdeti világítást biztosít az egész jelenet számára. A tárgyak minden csúcsát egyenletesen világítja meg, mivel nem függ semmilyen más világítási tényezőtől. Ez a legegyszerűbb és leggyorsabb típusú világítás, de a legkevésbé realisztikus eredményt ad. A fénymodell kiszámításához használt képlet szintén nagyon egyszerű, mert csak egy számtani művelet van - szorzás. A számításhoz elegendő az anyag színét megszorozni a világítás intenzitásával.
Vertex shader az egységes világítási modell kiszámításához:
Ez a legegyszerűbb shader egyszerűen kiszámolja az objektum helyzetét a világűrben, de ebben a világítási modellben nem használható, mert nincs szükségünk más összetevőkre (normál stb.) A csúcsra a számításhoz.
Itt is nincs semmi bonyolult, csak visszaadja a vektor termékét a fordítóhoz, egy bizonyos számhoz ebben az esetben a környezeti intenzitás. Ezt így teszi:
Az egységes világítási modell:

A fény elárasztó és diffúz komponenseinek kiszámításához három vektorra van szükség:
• Normál N a töredékre.
• A V fajkészlet olyan vektor, amely a megfigyelő felé irányul.
• A L fényforrás helyzete.
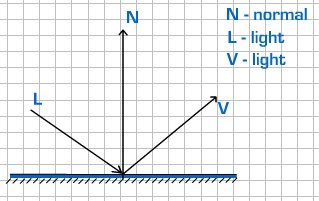
A vektorok közötti szögek a megvilágítás intenzitását alkotják.
2. A világítás diffúz modellje.
A diffúz világítási modell olyan fénymodell, amely a fényforrás és a tárgy normál felületétől függ. Mivel a fénysugárzás minden irányban megegyezik, a fajvektor nem számít, pl. v = 0. Ez a módszer több számítást igényel, mivel az az egyes objektumok csúcsain változik, de az objektumokat jól árnyékolja, és hangot ad. A fény nem esik az egész felületnek ugyanolyan színnel (mint korai megvilágítás esetén), de úgy tűnik, hogy a fény valamilyen felületre irányul.
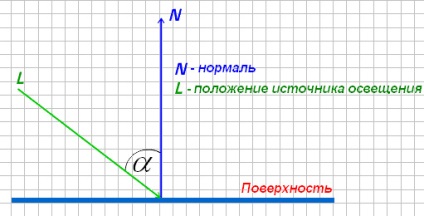
Ha a fényforrás helyzetvektora merőleges a felszínre, nem figyelhető meg a homályosság, mert a fény intenzitása a szögtől # 945; A megvilágítás diffúz modelljének kiszámításához a képletet (Lambert-törvény szerint) használjuk:
Összegezzük - hozzunk létre árnyékolókat a világítási számításhoz.
És a pixel shader:
Diffúz világítási modell:
3.Blikovaya modell a világítás.
Nehéz elképzelni egy ilyen világítási modellt anélkül, hogy meglátná. De valójában csaknem mindenütt láthatjuk ezt a modellt. Például egy tisztán polírozott (kör alakú) egyenes fémfelület, amely a fényforrásra mutat, és olyan szöget vetít, amely nem merőleges a felületre. Ennek eredményeképpen a felületen káprázást fogunk látni, ami jelentősen növeli a kép realizmusát. Ezek a tükrök a felszínről származó fényforrást tükrözik. Ebben a világítási modellben a fényforrás és a normál (pl. A diffúz megvilágítási modell esetében) vektorok mellett két további vektor is használható: a nézeti vektor és a reflexiós vektor. A Bui-Tuong Fong sugallta a látványos világítási modellt.
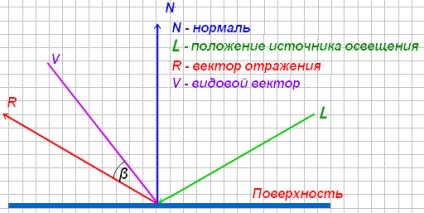
A fajvektor és a reflexiós vektor közötti szög - # 946;. Minél nagyobb a szög # 946;, annál világosabb a megvilágítás. Ezért a megvilágítás fújt modelljét az alábbi képlet adja meg:
ahol R = tükrözi (-norm (V), N)
n a lumineszcencia fénysűrűségi együtthatója.
A lumineszcencia fényerejének függése a szögben # 946;:
Az n növekedésével a reflexió egyre inkább felfrissül és egyre inkább koncentrálódik az R. reflexió vektor irányába.
Nem szükséges kiszámítani a nézet vektort az árnyékolóban, kiszámíthatja azt a programban, és beilleszteni a csúcsrétegbe. Ehhez invertálni kell a nézeti mátrixot és a D3DXVECTOR4 vektorral (0.0.0.0.0.0,1.0) vektorral kell szaporítani - a pozíció, amelyen a vektor merőleges a felületre (rám nézünk). Ez így néz ki:
Világítás modell:

Blinn világítási megvilágításának módosítása.
Jim Blinn alternatív megoldást adott a káprázás megvilágításának kiszámítására, ami kiküszöböli a drága számításokat a reflexiós vektoron. Bevezett egy köztes vektort, amely a fajvektor és a fényforrás pozícióvektorának átlagértéke: H = (L + V) / (| L + V |)
Az általános képlet a következő:
Ezért a fragment shader már így lesz:
A lumineszcencia fényerejének kiszámításának gyorsítása.
Schlick javasolta az n fokú helyettesítést. Hagyja, hogy a skaláris termék legyen D: D = (N • H) n. Ezután az ő módszere szerint a fény fényességét az alábbiak szerint kell kiszámítani:
Összehasonlító grafikonok a hatalmi törvényekről:
Valójában a fény visszaverődésének fizikai jelentése sokkal bonyolultabb, mint a Fong-megvilágítási modellben feltételezhető. Egy reálisabb modellben az L hullámhossztól és a fény előfordulásának szögétől függ (N • L). Ezt a függést Fresnel-együtthatónak nevezik.
Világító alkatrészek kombinációja.
Most három fénymodellt adhatunk hozzá (állandó, diffúz és fényes), hogy megkapja a teljes fénymennyiséget, amit a szemem kap:
A pixel shader most így fog kinézni:
A Cook-Torrance alapú realisztikus világítás
A reálisabb világítási modellekben a hangsúly az energiafogyasztás energiaeloszlásán alapul. Részét az anyag abszorbeálja és hővé alakítja, egy másik rész szétszóródik diffúz fényként, a harmadik rész a fényvisszaverődés felületét állítja be. Ezért a különböző anyagok esetében az incidens fényének elválasztása különböző módon történik, és attól függ, hogy:
• Normál elosztási funkciók
• Árnyékolás és szűrés
• A Fresnel-együttható
Normál elosztási funkció
Ez a függvény leírja a normál normálértéktől a felszínre eső lehetséges eltérést az ideális normál N értéktől. Minél inkább ez a funkció sekély, annál nagyobb az eltérés megengedett, és annál nagyobb a visszaverődő tükröződés helyének nagysága. A szükséges normálok az L + V vektor mentén helyezkednek el, és a V irányban láthatóak, a szög (H • N) pedig a néző számára. Cook és Torrence a Beckmann eloszlási képletet használta:
ahol d = H • N
m az objektum érdességének mértéke. 0,2f sima felület, 0,6f durva felület. Az alapértelmezett beállítás 0.3f.
A Beckmann forgalmazási ütemezése:
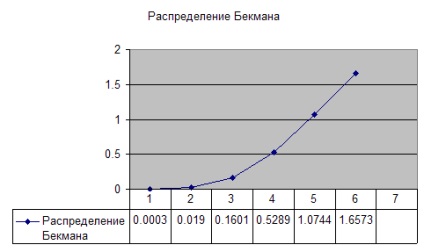
Árnyékolás és árnyékolás
A Cook-Torrance modell figyelembe veszi az olyan hatásokat is, mint az árnyékolás és a maszkolás, amelyek meghatározzák a vakító komponens intenzitását.
Árnyékolatlan fény:
Árnyék nélküli fény egyenlő:
Ezután a G végső tényezője:
Ez a tényező meghatározza a visszavert fény frakcióját, és ezt a függvény határozza meg:
ahol f az incidencia szöge, amelynek koszinusa c = (N • H)
n az anyag törésmutatója, g = sqrt (n 2 + c 2 -1)
Valójában a shader-ben a Fresnel együttható kiszámításához eltérő képletet használunk az utasítások korlátozása miatt. A helyettesítést a Schlick kínálta:
F = Rs + (1-Rs) × (1-E · N) n
ahol Rs a fényvisszaverődés,
E a megfigyelő vektora,
N normális a normál térképből.
Az ilyen közelítés nem veszi figyelembe az f és n komponenseket, hanem az n fokú, amelynek növekedésével nem lehet rossz eredményt elérni. A Schlick használt n = 5.
Összes multiplikátor kombinálása
Torrence és Sparrow kombinálta ezeket a tényezőket, és a káprázás kiszámításának képletét eredményezte:
Az N • V nevezőt bevezetjük a fény intenzitásának szabályozására.

A fény mennyiségének kiszámítására szolgáló általános képlet a következő:
A képletet egy kicsit egyszerűsítettük, mivel az eredetiben a megvilágítás minden egyes elemét (kivéve a fáklyát) F (0, n) szorozzuk. Ennek oka a Schlick közelítés használata.
Ennek a hatásnak a pixel shaderje: