Optikák és hullámok
A hullámelmélet keretein belül a Huygens-Fresnel-elv lehetővé teszi a fény egyenes vonalú terjedését. Határozzuk meg a fényhullám amplitúdóját egy tetszőleges P pontban, a Fresnel zóna módszerrel. Először egy incidens sík hullám esetét vizsgáljuk (5.2. Ábra).
Tegyük fel, hogy a végtelenben elhelyezkedő fényforrásból szaporodó F hullám síkja egy bizonyos időpontban egy távoli OP-r0-tól a P. megfigyelési ponttól.
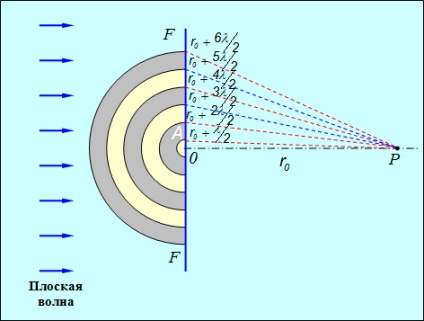
Ábra. 5.2. A Huygens-Fresnel elv alkalmazása síkhullámra: Fresnel zónák a felületen
sík hullámfrontot képviselnek a koncentrikus gyűrűk
(az egyértelműség érdekében a Fresnel zónák képét 90 ° -kal elforgatják, így a P pontból néznek ki)
Minden hullámfront pont szerinti Huygens elv - Fresnel elemi bocsátanak gömb alakú hullámok terjednek az egész fórumon, és egy idő után eléri a megfigyelési ponton P. A kapott rezgési amplitúdó ebben a pontban határozza meg a vektor összege amplitúdója összes másodlagos hullámok.
Az F hullámfront minden pontján fellépő oszcilláció ugyanazt az irányt eredményezi és ugyanabban a fázisban fordul elő. Másrészt az F elülső pont minden pontja a P ponttól különböző távolságokon van. A másodlagos hullámok amplitúdójának megfigyelési pontban történő meghatározásához Frenel egy módszert javasolt a hullámfelületnek a gyűrűs zónákra, a Fresnel zónákra való felosztására.
Ha a középpontot P pontként vesszük, egy sor koncentrikus gömböt állítunk elő, amelynek sugarai a hullámhossz felénél kezdődnek és minden alkalommal növekednek. Ha az F hullám sík felületével metszik egymást, ezek a szférák koncentrikus köröket adnak. Így a hullámok elülső részén a sugarak stb. Csengetési zónái (Fresnel zónák) jelennek meg.
Meghatározzuk a Fresnel zónák sugarait, figyelembe véve, hogy 0A 2 = AP 2 - 0P 2,
vagyis a P jelű megfigyelési ponton keletkező amplitúdó a hullámfront teljes felületén megegyezik a középső (első) Fresnel zóna által létrehozott amplitúdó felével. Így a p-pontban az F hullámfelületen okozott rezgéseknek ugyanolyan amplitúdója van, mintha csak az első (középső) zóna fele járna. Ennek következtében a fény szétszóródik, mintha egy keskeny csatorna, amelynek keresztmetszete megegyezik az első (központi) Fresnel-zóna felével - ismét egy síkhullám egyenes vonalú terjedésével jöttünk.
Ha azonban, ahogy az a hullámok, hogy a membránt egy lyuk, nyitva hagyva csak a központi (első) Fresnel zónában, az amplitúdó a P egyenlő A1, azaz kétszer meghaladja az amplitúdó által termelt összes hullámfront. Ennek megfelelően, a fény intenzitása, a P pont lesz négyszer több, mint annak hiányában közötti akadályok a fényforrás és a P pontban Meglepő, nem? De csodák nem történnek a természetben: más részein a fény intenzitása a képernyő fog gyengülni, és az átlagos fényerőt a teljes képernyőn, amikor a rekeszizom, amint az várható, hogy csökken.
E megközelítés érvényességét, amely a hullámfront Fresnel-zónákra való felosztását jelenti, kísérletileg megerősítést nyert. A páros és furcsa Fresnel zónák oszcillációi antiphase-ben vannak, és következésképpen kölcsönösen gyengítik egymást. Ha egy olyan lemezt helyezzünk a fényhullám ösvényére, amely lefedi az összes egyenletes vagy furcsa Fresnel zónát, akkor láthatjuk, hogy a P pontban a fény intenzitása élesen nő. Egy ilyen lemez, amelyet zenekarnak hívnak, úgy működik, mint egy gyűjtőlencse. Ismét hangsúlyozzuk: a Fresnel zónák a hullámfront felületének mentálisan elválasztott szakaszai, amelyek pozíciója a kiválasztott P megfigyelési ponttól függ. Egy másik megfigyelési pontnál a Fresnel zónák helyzete más lesz. A Fresnel-zóna módszer alkalmas arra, hogy bizonyos akadályok esetén megoldja a hullám-diffrakció problémáit.
Kétféle diffrakció létezik. Ha az S fényforrás és a P megfigyelési pont messze van az akadálytól, akkor az akadályon fellépő, és a P pont elérési sugarai közel párhuzamos gerendákat alkotnak. Ebben az esetben a párhuzamos sugarak diffrakciójára vagy a Fraunhofer diffrakciójára utal. Ha azonban a diffrakciós mintát a diffrakciót okozó akadály véges távolságától kell figyelembe venni, akkor az a gömbhullámok diffrakciójáról vagy a Fresnel-diffrakcióról szól.