Az elektromágneses indukció (1831 g
A mágneses indukció áramlása (mágneses fluxus).
Az önkényes felület eleme D S vektorként ábrázolható, számszerűen egyenlő a D S felületi elem területével, és a normális felület mentén irányul.
Definíció szerint a mágneses indukció fluxusa a DS felület egy elemén keresztül a B mágneses indukciós vektor skaláris terméke a D S. vektor által.
Használata vizuális képet erővonalak, azt mondhatjuk, hogy a mágneses fluxus egyenlő a sorok száma az erő a mágneses indukció, amely merőlegesen halad át a területen D S.
A mágneses fluxus dimenziója: [Ф] = Тл / м 2 = Вб (вебер).
A mágneses fluxus egy felületen mért nagysága idővel változhat két okból:
1. ha a mágneses indukció értéke változik, pl. B = B (t);
2. ha a mágneses mező vonalak áthaladnak, vagyis a felület mértéke, S = S (t).
Az elektromágneses indukció jelensége, hogy az F. mágneses fluxus minden olyan változása, amely egy zárt áramkörbe áramlik, az áramkörben lévő indukciós áram megjelenését okozza.
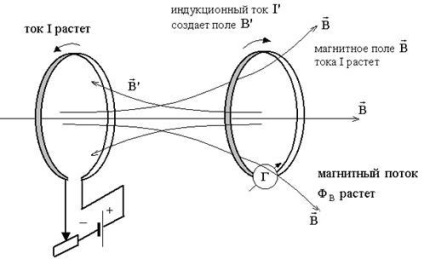
Ezt a Faraday-Lenz-törvény kimondja
Az indukció emf értéke megegyezik az ellenkező jelekkel vett mágneses fluxus változási sebességével.
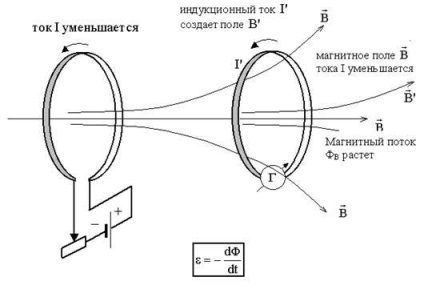
A Lenz-szabály szerint:
Az indukciós áramnak olyan iránya van, hogy az általa létrehozott mágneses mező meggátolja a mágneses fluxus megváltozását.
Az EMF indukció elektronikus mechanizmusa
Az ábra mozgatható oldalú keretet mutat. A mágneses mező irányult tőlünk.
Húzza a mozgó oldalt sebességgel. A Lorentz-erő a töltésnél + q
A töltés átadása a távoli távolságból, és a munka elvégzése.
Megtaláljuk Faraday törvényének megfelelően:
A keret mozgatható oldala "söpör" a dS = lvdt területen. majd
Az eredmény ugyanaz, mint:
Az EMF indukálásának elektronikus mechanizmusa a Lorentz erőkomponens munkája.
Vortex elektromos mező
Menjünk a keret mozgó oldalához kapcsolódó referenciakeretbe.
Ebben a referenciakeretben v = 0,. de a mágneses mező gyorsan mozog.
Mivel a töltés q álló helyzetben van, és a nagyteljesítményű erő hatással van az üres töltésű q-re. ezért ez az erő intenzitással hat az ELEKTROMOS TERÜLETEN.
Ennek az elektromos mezőnek a forrása nem töltődik be, mint a statikus esetben, hanem mozgó mágneses mező. Az ilyen elektromos mezőt örvénynek nevezik, mivel a vonalai feszülnek. A vortex mező munkája a zárt kontúr mentén történő áttöltésnél nem nulla (ellentétben az elektrosztatikus mezővel).
Néhány kísérleti tény
Vegyünk néhány kísérleti tényt:
- Az állandó mágneset a tekercsbe helyezzük, a galvanométerre zárva, vagy kivesszük. Amikor a mágnes az áramkörben mozog, elektromos áram
Hasonló eredmény fordulhat elő egy mozgó elektromágnes esetében, amelyen keresztül egy egyenáram áramlik át az elsődleges tekercshez képest, vagy amikor az álló helyzetű másodlagos tekercsben lévő áram megváltozik.
- a galvanométeren zárt keretet egy egységes mágneses mezőre helyezzük és forgatjuk. A keretben elektromos áram jelenik meg. Ha a keret az erővonalak átlépése nélkül mozog, akkor az áram nem merül fel.
- a keret egy inhomogén mágneses mezőben mozog. A kereten áthaladó indukciós vezetékek száma változó. A keretben elektromos áram jelenik meg.
Az áramkörben megjelenő áram, amikor a mágneses fluxus változik, indukciós áramnak nevezik.
A zárt hurkú elektromos áram létezésének feltétele egy elektromotoros erő jelenléte, amely fenntartja a potenciális különbséget. Következésképpen, amikor egy zárt áramkörön átáramló mágneses fluxus megváltozik, benne egy EMF keletkezik, amelyet az indukció EMF-jének (e i) neveznek.
Így az elektromágneses indukció jelensége az áramkörben lévő EMF megjelenéséből áll, az áramkörbe kerülő mágneses fluxus változásával.
Ha a hurok zárva van, akkor az indukció EMF egy elektromos indukciós áram jelenlétében nyilvánul meg
I = e i / R. ahol R a hurokellenállás.
Ha a hurok nyitva van, potenciális eltérés következik be a vezető végénél, egyenlő az ej-vel.
Az áramkör indukciós áramának irányát a Lenz-szabály határozza meg:
Az induktív áramot úgy irányítják, hogy mágneses mezője ellenálljon a mágneses fluxus változásának, amellyel okozza.
Az indukciós áram iránya a következő:
- állítsa be a külső mágneses mező B. irányát.
- meghatározza, hogy a külső mező mágneses indukciós vektorának ingadozása nő vagy csökken.
- a Lenz szabály szerint jelezzék a B i indukciós áram mágneses indukciós vektorának irányát.
- a megfelelő csavar szabályával határozza meg az áramkör indukciós áramának irányát.
Az önindukció az elektromágneses indukció különféle megnyilvánulásait jelenti.
Vegye figyelembe az aktuális forráshoz csatlakoztatott áramkört (6. ábra). Az áram folyik az áramkörön, ez a mágneses mező a környező térben keletkezik. Ennek eredményeképpen a kontúrat a belső M-mágneses fluxus hatja át. Nyilvánvaló, hogy a belső mágneses fluxus arányos a mágneses mezőt létrehozó áramkörben:
Az L arányossági együtthatót az áramkör induktivitásának nevezik. Az induktivitás a vezető méretétől, alakjától, az élelmiszer mágneses tulajdonságaitól függ. Az induktivitás mértékegysége SI rendszerben - 1 Henry (HH).
Ha megváltozik az áramkör áramköre, akkor az önmágneses fluxus Фс is változik. Az FF értékének változása egy EMF indukálását eredményezi a kontúrban. Ezt a jelenséget önindukciónak nevezik, és a megfelelő érték az öninduktancia EM e.
Adjuk meg a kontúrnak az aktuális I értéket A kontúron keresztüli mágneses fluxus arányos az aktuális I.
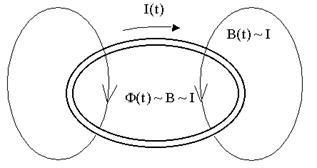
A jelenlegi és az aktuális kapcsolat közötti összefüggést írhatja:
itt L az áramkör induktivitása, [L] = TH (henry).
Ha ≠ const. I = I (t), akkor Φ = Φ (t), és egy indukciós emf keletkezik, a
ha L = const. az
Ennek eredményeképpen a változó külső mezőtől származó ferromágnes mezőfüggése egy hiszterézis hurok formájában van, amelyet a B-H tengelyek ábrázolnak.
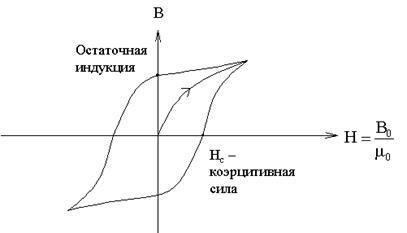
A vektort mágneses térerősség vektornak nevezzük. Segéd jellegű, a mágneses mező erőssége a mágneses indukció vektora. A vektorok közötti kapcsolat és a következőképpen íródik: