Számjegyekkel ellátott vetületek
UDC 514.1 (076) BBK 22.151.3 I7
A bíráló az "Építőtermelés és anyagok" osztály vezetője, S. V. Maksimov
Jóváhagyta az egyetem tudományos és módszertani tanácsa módszertani kézikönyvének szakasza.
Számjegyekkel ellátott vetületek. módszeres utasítások a diákok önálló munkájára / Comp. A. Yu. Lapshov, L. Sidorovskaya L., V. I. Churbanov
Kidolgozta összhangban jóváhagyott programja fegyelem „ábrázoló geometria és rajz”, és a SES a HPE tananyag UlSTU specialitás 290300 „Design Építészeti környezet” 270 109 „ipari és mérnöki” 270109 „Heat és a szellőztetés.”
A módszertani útmutatások az oktatás minden formája szakosodott hallgatók számára készültek. Ezek tartalmazzák a numerikus jelekkel ellátott előrejelzések fő elméleti adatait, amelyek magukban foglalják a kontroll kérdéseket és feladatokat, mintaoldalakat.
UDC 514.1 (076) BBK 22.151.3Â7P 79
1. A PROJEKCIÓK MEGHATÁROZOTT MEGÁLLAPÍTÁSAI SZÁMÚ MEGJEGYZÉSEK ......... ..5
1.1 Pont és egyenes vonal a számjegyekkel ellátott vetületekben ............................ 5
1.2 A sík számjegyekkel ellátott vetületekben ........................................... 8
1.3 A numerikus jelekkel ellátott vetületek felülete ....................................... .12
1.4 Topográfiai felület ................................................................ 15
2. IRÁNYELVEK AZ EPSU TELJESÍTMÉNYÉRE
3. PÉLDA AZ EHURUS TELJESÍTMÉNYÉRŐL .................................. .............................. 19
3.1. A lejtőintervallumok meghatározása a töltés és a közutak feltárásához ............................ 19
3.2 Egy földszerkezet egyenes vonalú lejtői metszésvonalának megépítése. 20
3.3 Az egyenes vonalú és a lejtős lejtők metszésvonalának kialakítása ...... ..20
3.4 A terület és az út lejtői metszésvonalának megépítése ........................... .20
3.5 Az ásatás határának meghatározása .................................... .21
3.6 A topográfiai felület profilja és szerkezete .................. .. 22
4. A HASZNÁLT FELTÉTELEK SZÓJEGYZÉKE ................................................... .24
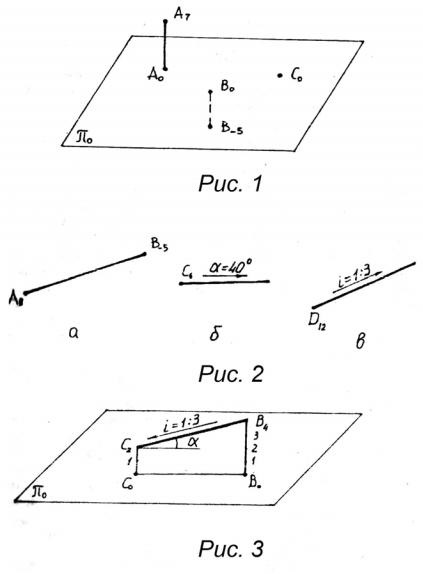
Az építőiparban olyan tárgyak vannak, amelyeknek a tervei jelentősen meghaladják a többiet. Például részeit a földfelszín található rajtuk szerkezetek, utak, töltések különböző, repülőterek, építkezéseken, és így tovább. F. A tervezési ilyen létesítmények használjon hagyományos merőleges vetülete kivitelezhetetlen. Ilyen esetekben, a nyúlvány használunk általában numerikus jelölések, melyek azzal jellemezhetők, hogy eredményeként keletkezett a merőleges vetülete a tárgy rá a vízszintes síkban, az úgynevezett zéró-síkban. Ahhoz, hogy egy képet, egyedileg megfelelő témát, hogy a megfelelő pontok a nyúlványok levelet szám jelzi a magasságot (általában méterre) a mérési pontok zérussík, ezek a számok az úgynevezett numerikus jelölések (1.).
1. Milyen objektumok tervezése során numerikus jelölésekkel számolnak?
2. Hogyan alakulnak ki számokból álló vetületek?
3. Mi a neve a síknak, amelyből a pontok magasságai számítanak?
1. A PROJEKCIÓK ELMÉLETI ALAPJAI SZÁMÚ MEGJEGYZÉSEKkel
1.1. Pont és vonal számsorozatokban
Mivel egy kiemelkedés lehetetlen meghatározni a tényleges helyzet egy pontot a térben, a pontokat a kivetített védjegyek numerikus kódokat használnak, amelyek meghatározzák a távolság a lényeg, hogy a vetítési sík, az úgynevezett előrejelzések numerikus jegyekkel zérussík (π 0). Ezek a kódok, vagy az úgynevezett jelek vannak írva a jobb és alján a levél kijelölő pont, és lehet pozitív vagy negatív attól függően, hogy a pont felett vagy alatt a nulla síkot, például a 7. B -5. C 0 (lásd az 1. ábrát). A numerikus jelekkel ellátott vetületek rajzai általában lineáris skálán vannak megadva.
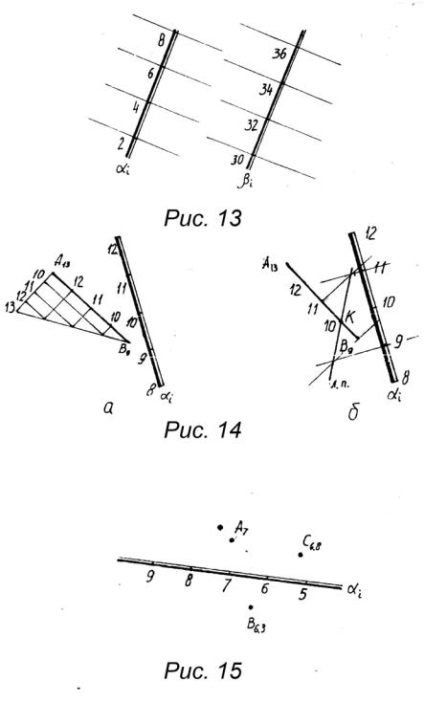
Közvetlen a kiemelkedések numerikus jelölések is által meghatározott két pont (2A.), Vagy egyetlen ponton, de ebben az esetben kell további információt az irányt hajlási szög csökkenése irányában pont és egy egyenes vonal a nulla szintű síkot (π 0). Ezt a problémát oldja prostanovkoy mutató nyilak jelzik jelek és csökkenti a dőlésszög egy egyenes vonal síkjához π 0 (2B.). Gyakran előfordul, hogy ahelyett, hogy a hajlásszög sokkal kényelmesebb használni a koncepció lejtő, a lejtő jelöli az i és úgy definiáljuk, mint egy érintőt hajlásszöge síkjára π 0. Amint a 3. ábrán látható, egy előfeszítő vonal CB egyenlő az arány a különbségi értékek B 0 és B 4 C 0 C 4 méretre E vonal vízszintes vetülete a π 0 síkra
Mivel a vízszintes hossza a nyúlvány (a nyúlvány a síkra π 0) a nyúlványok számszerű jegyekkel nevezzük annak elhelyezése, és a különbség kezdetét és végét a szegmens azt mondta, hogy a felesleges, a rövidebben lejtő intervallum említhetjük aránya meghaladja azt fúráshoz.
Egy másik fontos koncepció, amely a vonalat jellemzi a numerikus jelek előrejelzéseiben, egy intervallum fogalma. Egy intervallum egy adott vonal szegmensének elhelyezése, amelyben az elején és a végén levő jelölések különbsége egyenlő. Az intervallumot I betű jelöli. Ily módon a meredekség és az intervallum kapcsolódik az i = 1 / I reléhez.
Gyakran előforduló problémák egyenes vonalra és numerikus jelölésekkel rendelkező előrejelző pontokra a következők:
1. Egyenes vonal elérése. Az egyenes vonalának osztályozása egy olyan egyenes pontok meghatározását jelenti, amelyek egész számokkal jelöltek és egy egységnyi hosszúságúak. Az egyenes vonalának befogadását a 4. ábra mutatja, itt két eset lehetséges:
a) ha a szegmens mindkét vége ugyanazokkal a jelekkel rendelkezik (4. ábra, a, b). Ebben az esetben, a végén az intervallum nagy pontossággal feküdt merőleges, és a különbség értéke védjegyek hajtjuk grafikai komplexitású a 4. ábrán látható is. Ha a végpontok frakcionált jelek a végén a szegmenst egy alsó jelzése feküdt csak tört része, de a másik feküdt a különbség a jelek, valamint a törtrész végét a szegmens. Az átsorolás a 4. ábrán látható, b.
b) abban az esetben, ha a szegmensek végeinek különböző jelei vannak. A szerkezetek csak abban különböznek egymástól, hogy a szegmens kezdete és vége ellentétes irányban helyezkedik el. Ilyen érettségi példa a 4. ábrán, c.
2. A keresztező szegmensek kölcsönös helyzetének meghatározása. A szegmensek kölcsönös helyzetében vannak egymást keresztező, átjáró és párhuzamos szegmensek. Annak meghatározása érdekében, hogy a szegmensek metszenek vagy metszenek egymással, elegendő méretezésük és a versenyző pontok jelölésének meghatározása, ha e pontok
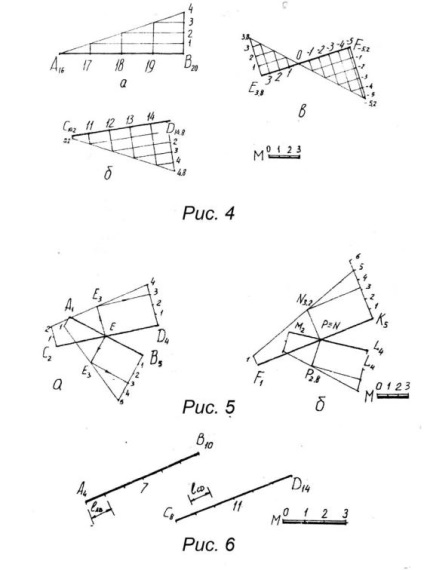
ugyanazok (az E pont az 5. ábrán, a), akkor a szegmensek metszi egymást. Abban az esetben, ha a versenyző pontok jelzései eltérőek (az 5. és a b) pontban szereplő N és P pontok, a jelek átkerülnek.
A vonalak párhuzamosságának tisztázása csökkenti a következő feltételek ellenőrzését: a) a szegmensek elhelyezkedése párhuzamos egymással; b) a növekvő és csökkenő jelek iránya megegyezik;
c) a szegmensek intervalluma (lejtése) azonos. Tehát a 6. ábrán bemutatott A 4 B 10 és C 8 D 14 szegmensek párhuzamosak, ha az AB AB intervallum. egyenlő lesz a CD ℓ intervallumával. így e sorok párhuzamosságának első két feltétele már teljesült.
1. Milyen további paramétert jelöl meg a numerikus jelölésekkel ellátott vetületi betűjel?
2. Hogyan lehet egy egyenes vonalat előrejelezni numerikus jelekkel?
3. Mi az úgynevezett torzítás, ültetés, felesleg és intervallum?
4. Mit jelent az egyenes egyenesítése?
5. Hogyan lehet megkülönböztetni a keresztezett egyenes vonalakat a metszéspontoktól a numerikus jelölésekkel?
6. Melyek a vonalak párhuzamosságának jelzései a numerikus jelölésekkel?
1. Ha a szegmens intervalluma 5, akkor mi ez a szegmens lejtése?
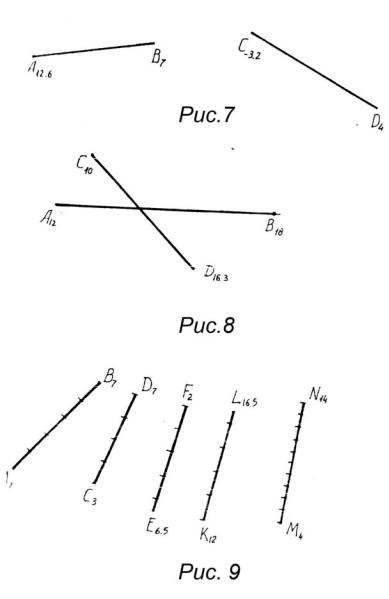
2. Végezze el a 7. ábrán látható sorokat.
3. Határozza meg az A 12 B 18 és C 10 D 16.3 egyenesek kölcsönös helyzetét.
4. Határozza meg, melyik a 9. ábrán látható vonalak párhuzamosak?
1.2. A sík számjegyekkel ellátott előrejelzésekben
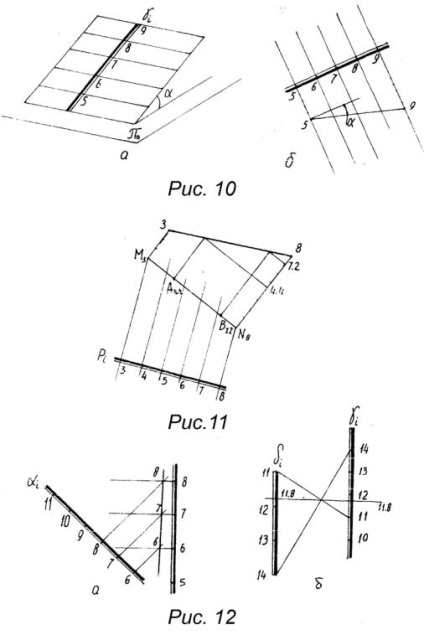
A numerikus jelekkel ellátott vetületek síkját a legnagyobb meredekség lineáris vonala adja, amely ebben az esetben a sík lejtése. A 10. ábrán egy γ i sík az α-szöggel halad át a π 0 síkkal. A síkot a lejtési skála mutatja, amelyet két párhuzamos vonal jelez, amely megvastagodott és vékony, és a sík kontúrjai. A vízszintes egy szintvonal. a síkban fekve és a vetület vízszintes síkjával párhuzamosan, pontjai ugyanazokkal a jelekkel rendelkeznek.
Általában a horizontális felületeket a teljes felületen állandó magasságszélességgel húzzák át. Amikor egy volumetrikus rajzról síkdiagramra (10. ábra, b) változik, akkor a sík meredekségszögének értékét a legnagyobb meredekség sorának osztályozásával határozzák meg. A numerikus jelzésekkel ellátott síkok síkjában gyakran előforduló problémák a következők:
1. Egy egyenes és egy pont egy síkra való tagolásának meghatározása.
A 11. ábra mutatja az A 4.4 B 7.2 egyenes vonalat és a P i síkot, hogy megoldja azt a kérdést, hogy ez a vonal a P i síkhoz tartozik-e, és kiterjeszti-e a sík körvonalainak metszéspontjára. Feltételezve, hogy a vonal a síkhoz tartozik, az M és N metszéspontok a 3. és a 8. jelöléssel vannak ellátva. Az M 3 N 8. egyenes osztályozás elvégzésével elvégezhető
hogy az A és B pontok ezen a ponton kapott pontjai megegyeznek a megadott értékekkel, ami azt jelenti, hogy az A 4.4 B 7.2 egyenes vonal P i síkhoz tartozik.
Annak megoldása érdekében, hogy egy adott pont a síkhoz tartozik-e, ebben a síkban egyenes vonal (ebben az esetben a szomszédos vízszintes vonalak között). Az egyenes vonal felosztásával határozza meg az adott pontnak megfelelő vonal pontjának jelölését. Ha a pontok jelzései megegyeznek, a pont a síkhoz tartozik.
2. A síkok metszésvonalának megrajzolása numerikus jelölésekkel. Tekintsük az általános esetet, amikor a lejtő skála nem párhuzamos (12. ábra, a). mert
Elég, hogy megoldja az adott síkok horizontjának problémáját. A kontúrok metszéspontjainak jelölése ugyanazokkal a jelölésekkel történik, biztosítjuk, hogy ugyanazon az egyenes vonal mentén fekszenek. Ez a vonal a síkok metszéspontjának vonala.
A helyzet abban különbözik, hogy a szóban forgó síkok meredekségének mérete párhuzamos (12b. Ábra). Ebben az esetben a meredekség skálájával egyenes vonalakkal, azonos pontszámú tetszőleges párospontokkal kombináljuk a metszéspontjukat. A síkok metszéspontja ezen a ponton is átmegy a síkok meredekségének merőleges síkjára.
3. A síkok párhuzamosságának meghatározása (13. ábra).
A síkok párhuzamosságának meghatározásakor a paraméterek ellenőrzését a következő jellemzőkkel összhangban végzik el:
a) a lejtés párhuzamos; b) a síkok lejtői egyenlők; c) a süllyedés iránya ugyanaz;
Így a 13. ábrán bemutatott síkok kielégítik, és ezért párhuzamosak.
4. Egyenes és sík metszéspontjának meghatározása.
Tegyük fel, hogy megkapjuk az a i síkot és az A 13 B 9 vonalat. Keressük a metszéspontjukat. A probléma megoldása érdekében előprogramozzuk az egyenes vonalat (14. Ezután helyezze azt egy általános síkra, ami elvégzi ezt a vízszintes síkban tetszőleges jel vonal (ábra. 14b). Miután megtaláltuk az általános pozíciós sík körvonalainak metszéspontjait és az adott sík α i kontúrjait. meghatározzuk azokat a pontokat, amelyeken keresztül a síkok metszésvonala halad. A vonal metszéspontjánál az adott vonal A 13 B 9 az egyenes és a sík metszéspontjának kívánt K pontja. Melyik része a vonal látható, és mi nem, mi határozza meg az arány védjegyek kontúrok síkban α i és jelölések A és B pontok Látjuk, hogy a védjegy pont (13) 11 és 12 között alakos síkja tehát magasabb, mint a sík és az egyenes szakasz az A 13-tól a K pontig látható.
1. Hogyan definiálható a sík numerikus jelölésekkel?
2. Mi a vízszintes sík?
3. Hogyan alakul ki a síkhoz tartozó pont numerikus jelölésekkel rendelkező előrejelzésekben?
4. Melyek azok a lehetséges esetek, amikor megoldják a síkok metszésvonalának megépítésének problémáját?
5. Melyek a síkok párhuzamosságának jelzései numerikus jelölésekkel?
6. Hogyan viszonyul egy egyenes egy részének láthatósága egy síkhoz?
1. Határozza meg, hogy a pontok A 7-nek tartoznak-e. B 6.3. Az α i sík C.8,8 (15. ábra).
2. Oldja meg az α i és β i síkok párhuzamosságának kérdését. γ i és δ i (16. ábra).
3. Határozza meg az A 12 B 16 egyenes és az α i sík metszéspontját (17. ábra).