Quine és Quine módszerek
A Quine módszer az íráshoz kötődik, nem minden lehetséges függvényt, hanem csak azokat, amelyek egy adott függvény DNF-jében jelen lehetnek. Feltételezzük, hogy a függvény egy CDNF formájában van megadva. Ebben a módszernél a n-edik elemi konjunktúrákat a DNP-ben n értékű minternek nevezik.
A Boole-függvény Quine-módszerrel és a továbbfejlesztett Quine-McCluskey módszerrel történő minimalizálási problémájának megoldása a fogalmak fogalmára és azok rendszereire épül.
Az algoritmus a logikai függvény MDNF minimális diszjunktív normál formájának megszerzéséhez:
1. A logikai függvény megjelenik a CDNF-ben. Továbbá, ha azt egy igazságtáblázat határozza meg, akkor azokat "egységek szerint" írják le; ha egy algebrai önkényes diszjunktív formában adják meg - telepítési műveletek alkalmazásával, De Morgan képletekkel stb.
2. A kapott CDNF-ben minden hiányos kötés, majd abszorpció elvégezhető. Ennek eredményeképpen csökkentett diszjunktív normál formát kapunk, azaz a legrövidebb összes elemi termék (egyszerű implikáns) diszjunkciója, amely egy adott logikai függvénybe lép.
Adjuk meg az adott funkciót az SDNF-ben. A rövidített formára történő áttérés két művelet következetes alkalmazásán alapul: ragasztási műveletek és abszorpciós műveletek.
A ragasztási művelet kifejezésben való megjelenítéséhez a formanyomtatvány párja és. csak az egyik argumentumban különbözik az egyik kifejezésben inversion nélkül, míg a másikban az inversion. Ezután összeragasztjuk az ilyen pár kifejezéseket :. és a beillesztés eredményeit a függvény kifejezése további kifejezéseként jeleníti meg. Ezután elvégzik az abszorpciós műveletet. Ez a kifejezésen alapul: (a tag elnyeli). A művelet viselkedésében a ragasztási művelet eredményeként létrejött kifejezések által felvett összes tagot törlik a logikai kifejezésből. A ragasztási és abszorpciós műveleteket a lehető leghosszabb ideig hajtják végre.
3. Keresse meg a minimális diszjunktív normál formákat (MDNF) a befogadó mátrixból.
Az implicit mátrix olyan táblázat, amelynek függőleges és vízszintes bemeneteit a CDNF tagjai és az adott logikai függvény egyszerű implikátorai rögzítik.
A nevezett mátrix sejtjeit, melyeket a sorok és a CDNF abszorbens tagjaival rendelkező befoglaló és oszlopok keresztezésével alakítottak ki, keresztezéssel vannak jelölve [5].
Az MDNF-t úgy találjuk, mint a befoglaló minimális számának diszjunkcióját, amelyek együttesen kiterjednek a befoglaló mátrix minden kereszt oszlopára.
4.1. Példa. A logikai függvény minimalizálása:
Megoldás: 1. A függvény algebrai formában jelenik meg telepítési műveletekkel
hat tagból álló CDNF-t kap:
2. A ragasztási műveleteket az alábbi sorrendben végezzük:
1) minden lehetséges ragasztás az első kifejezéssel együtt a többiekkel;
2) a második ciklus minden lehetséges ragasztása a többivel, az 1. kivételével;
3) elvégezzük az összes lehetséges ragasztást a harmadik kifejezéssel a többivel, az 1. és a második kivételével stb.
Csak azokat a tagokat lehet összeragasztani, amelyeknél a negációk változóinak száma egyenként különbözik.
A ragasztás és felszívódás eredménye:
A csillagokat a CDNF azon tagjai jelölik ki, amelyeket a ragasztás után képződött termékek abszorbeálnak.
A vizsgált példában mind a hat kezdeti kifejezés abszorbeálódik, ezért az adott funkció SDNF formája:
Ebből a kifejezésből a ragasztás és az abszorpció műveletei nem alkalmazhatók, következésképpen a logikai függvény rövidített diszjunktív normális formája, és kifejezései egyszerűek.
3. Az adott függvényhez egy implicit mátrix van kialakítva (4.1. Táblázat).
Egyszerű implikátorok (minterms)
Az MDNF megszerzéséhez feltétlenül meg kell találni a befoglaló minimális számát, amelyek együttesen magukban foglalják a befogadó mátrix összes oszlopát keresztekkel:
A logikai függvény komplexitását a kifejezésbe lépő változók száma határozza meg: egy adott 14 függvényben, a minimális 9 függvényben.
Az első algoritmus egy logikai függvény minimális kötődési normál formájának (ICPF) megszerzésére:
1. A logikai funkció az SKNF-ben van ábrázolva. Továbbá, ha azt egy igazságtáblázat adta, akkor azt "nulla" írja; ha az algebrailag tetszőleges konjunktív formában van megadva, akkor minden lehetséges telepítési művelet végrehajtásra kerül az SKNF-hez való íráshoz.
2. A kapott SKNF-ben a hiányos kötés és az abszorpció minden lehetséges műveletét végezzük. Ennek eredményeképpen rövidített konjunktív normális alakot kapnak, amelynek tagjai egyszerű maszkok.
3. Az ICPF-t a muckstrom mátrix találja meg.
4.2. Példa. A logikai függvényt egy igazságtáblázat határozza meg. Keresse meg az ICPF-et ennek a funkciónak.
5. A logikai funkció ICPF :.
A második algoritmus az ICNF logikai függvény megszerzéséhez:
1. A logikai függvény az SDNF-ben egy adott függvénygel van ábrázva, negálva.
Ha a függvény egy igazságtáblával van megadva, akkor írja le az összes érvből számos terméket, és kapcsolja össze őket a diszjunktúra jeleivel; a termékek száma megegyezik azokkal a készletek számával, amelyeken az adott funkció eltűnik; mindegyik termék alatt írjon egy olyan argumentumcsomagot, amelyen a függvény nulla, és a nullával egyenlő érvek fölé helyezve a negáció jeleit.
Ha a függvény tetsz˝oleges formában algebrailag van megadva, elõször a CDNF találja meg, majd megírja az összes SDNF-ben nem szerepl˝o argumentum termékének diszjunkcióját.
2. Keresse meg az MDNF-et a fent leírt algoritmus segítségével.
3. A beérkezett MDNF-ből tagadják, és a De Morgan formuláinak átalakulása után megkapják az ICPF-et.
4.3. Példa. Keresse meg az ICNF-t, az igazságtábla által adott funkciókat.
3. MDNF, negatív módon:
4. Az utolsó egyenlőség mindkét oldaláról való tagadás és a De Morgan-képlet alkalmazásával az ICNF logikus függvényt kap:
A Quine módszerben van egy jelentõs kellemetlenség, amely összefüggésben van azzal, hogy szükség van a minterek teljes párhuzamos összehasonlítására a csökkentett konstrukció szakaszában. DNF. 1956-ban McCluskey javasolta a Quine módszer első szakaszának korszerűsítését, ami jelentősen csökkenti a minterm összehasonlítások számát [17].
A McCluskey-módszer ötlete a következő. Valamennyi minternek bináris számok formájában vannak írva, például 1010-nél. Ezek a számok csoportokba vannak sorolva a helyiségben lévő egységek számának megfelelően, vagyis az i-os csoportban vannak olyan számok, amelyek rekord egységükben vannak. A párhuzamos összehasonlítást csak a szomszédos csoportok között végezzük, mert A minőségi, ragasztásra alkalmas, csak egy kisülés esetén különböznek egymástól. Ha a minterumok nullától nagyobb fokozatokból vannak kialakítva, egy kötőjelet helyeznek el a kizárt változóknak megfelelő számjegyekbe.
Az eljárás a következő lépéseket tartalmazza a redukált DNF előállításához.
1. Elsődleges befoglalók keresése. A függvény minden mintermét egymás után nézzük meg, és egy műveletet végezzünk el minden minővel együtt, amellyel lehetséges. Az n-edik rang mintermei ragasztásának eredményeként minterms (n -1) -ga rangot kapunk. A ragasztási műveletben részt vevő n-edik fokozatok mintaképei például egy csillaggal vannak megjelölve. Ezután a minterms (n -1) -fokot vesszük figyelembe, és a ragasztási műveletet alkalmazzuk rájuk. A ragasztóminterms (n-1) -réteg átfedésben van, az így kapott minterm (n-2) -ta ragasztó stb. A színpad véget ér, ha az l-es sor újonnan nyert mintermei nem ragadnak össze. Minden jelöletlen minternek elsődleges implikátornak nevezzük őket. A diszjunkció egy rövidített DNF függvény.
Ezután a negyedik osztály mintermei összeragasztódnak, és újra ragasztják a mintereket csillagokkal jelöltük:
A második fokozat mintaképei:
Az elsődleges (egyszerű) fogalmak:
2. A védjegyek elrendezése. Ehhez a funkcióhoz a rövidített DNP:
A zsákutcák DNF és Sokr. A DNF-nek extra intervallumokat kell dobnia. Megépít egy táblát, amelynek sorai megfelelnek az elsődleges nevezőknek és oszlopoknak az SDNF minisztereihez. Ha a minta egy része tartalmaz egy befoglalót, akkor egy címkét helyeznek el a megfelelő sor és oszlop metszéspontjában.
3. Az alapvető lényegi tényezők megtalálása. Ha egy oszlopban csak egy egység van, akkor az elsődleges jelzőt, amely meghatározza ezt a sort, elengedhetetlen. Például alapvető jelentőségű. Egy lényeges következtetést nem lehet eltávolítani a Socrates-ből. DNF, t. Csak ő tudja ellátni a CDNF néhány miniszterét. Ezért azok a sorok, amelyek megfelelnek ezeknek a névsoroknak és oszlopoknak, amelyeknek vannak ilyen sorai, kizárásra kerülnek a táblázatban.
Ebben a példában a sorok és oszlopok nem szerepelnek
Ennek eredményeként megkapjuk a táblázatot:
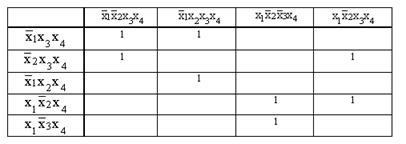
4. Extra oszlopok és sorok törlése. Ha a kapott táblázat ugyanazokkal az oszlopokkal rendelkezik, akkor mindegyikük csak egy törlésre kerül. Ha utána üres sorok vannak a táblázatban, azok is törlődnek.
5. A minimális lefedettség kiválasztása maximális intervallumokkal. A megjelenő táblázatban olyan sorok gyűjteményét választja ki, amelyek tartalmazzák az egységek összes oszlopát. A választás számos lehetséges változatával a változatot a lapot alkotó vonalak minimális számával lehet előnyben részesíteni. A táblázat minimális lefedettségét a következõknek felel meg. Ezután az MDNF így néz ki:
4.4. Példa. Minimáljuk a táblázatban megadott funkciót.
A tagok (az egyes kifejezések és az összes későbbiek) párhuzamos összehasonlítása feltárja a fogalmak ragasztási párját:
1. és 4. tag (ragasztás eredménye)
2. és 3. tag (ragasztás eredménye)
Második és negyedik tag (a ragasztás eredménye)
3. és 5. tag (a ragasztás eredménye)
4. és 5. tagok (a ragasztás eredménye)
A ragasztási művelet eredményeit bevezetjük a függvény kifejezésébe, és elvégezzük az eredeti kifejezés kifejezéseinek abszorpcióját:
Ismételjük a ragasztás és a felszívódás működését.
Itt a ragasztási művelet két párral történik: és. és. és a további ragasztás lehetetlen, ez rövidített forma (és ebben a példában a minimális forma)
Ebben a funkcióban ezek egyszerűek