Iteratív képlet - stadopedia
A (6) képletben a normál vektor a komplex csúcsa és súlypontja közötti távolságot jelöli. és a (6) képlet maga határozza meg a komplex csúcsainak átlagos távolságát a gravitációs centrumhoz.
A (7) képletben a komplex csúcsaiban a függvény () függvény átlagértéke van. és a képlet (7) maga határozza meg a függvény () függvényeinek átlagos eltérését a komplex csúcsánál ebből a középértékből.
A komplexek módszerét az 1. ábra szemlélteti. 3, amely a Himmelblau függvény szintvonalainak töredékét mutatja. Az ábrán az eredeti komplexnek csúcsai vannak. [1, 4]. A komplex csúcsának kiterjesztésével való visszaverődés után, amelyben a függvénynek a maximális értéke van, egy csúcspontot tartalmazó komplexet kapunk. [1, 4]. Tükrözés után a komplex tetejének nyújtásával. ahol a függvénynek maximális értéke van, akkor egy komplexet kapunk csúcsokkal. [1, 4].
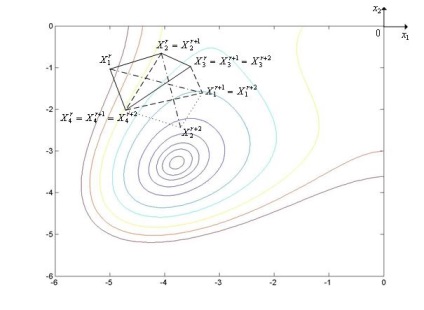
Ábra. 3. A komplex módszerrel a Himmelblau-függvény minimális keresésének nyomvonala.
A komplexek módszerének számos módosítása van, különösen a komplexum "lekerekítése" leküzdésére a keresési folyamatban. Ebből a célból egy meghatározott számú iterációval meg lehet találni a komplex maximális és minimális átlóit, és ha ezek aránya meghaladja az előírt értéket, akkor a megfontolt séma szerint új komplexet állítunk elő.
8.3 Az ismétlődő véletlen keresés módszere
A helyi feltétlen optimalizálásnak a következő többdimenziós problémáját tartjuk szem előtt: megtaláljuk a minimálisan az optimális kritériumot (), amelyet a -dimenziós euklideszi térben határozunk meg,
Az ismétlődő véletlenszerű keresés (háromlépéses módszer) módszerében egy iteratív sémát alkalmaznak (lásd az 1. ábrát)