Interpolációs mód
Eddig megvitattuk a tanulási algoritmust, amelyben csak egyetlen neuron Kohonen aktiválódott minden bemeneti vektor számára. Ez az akkreditációs módszer. Pontossága korlátozott, hiszen a kimenet teljesen csak egy neuron Kohonen funkciója.
Az interpolációs módszerben a legnagyobb hozamokkal rendelkező Kohonen neuronok egész csoportja képes továbbítani a kimenő jeleket a Grossberg rétegre. Az ilyen csoportokban lévő neuronok számát a feladattól függően kell kiválasztani, és nincs meggyőző adat a csoport optimális méretéről. Ha egy csoport olyan, a kimenet több NETrassmatrivaetsya a vektor, amelynek hossza normalizálják egység elosztjuk az egyes értékek NETna négyzetgyöke négyzetösszegét értékek NETv csoport. A csoporton kívüli neuronok nulla kimenettel rendelkeznek.
Az interpolációs módszer képes összetettebb találatok létrehozására, és pontosabb eredményeket adhat. Ennek ellenére nincs olyan meggyőző adat, amely lehetővé tenné az interpoláció és az akkreditáció módjának összehasonlítását.
A képzett hálózat statisztikai tulajdonságai
A Kohonen tanítási módszer hasznos és érdekes képességekkel rendelkezik arra, hogy a statisztikai tulajdonságokat különböző bemeneti adatokból nyeri ki. Amint Kohonen [8], a teljes mértékben képzett hálózati valószínűsége, hogy egy véletlenszerűen kiválasztott bemeneti vektort (összhangban a sűrűségfüggvénye a bemeneti állítva) legközelebb a bármely adott tömeg vektor 1 / k, ahol k - neuronok száma Kohonen. Ez a súlyok optimális eloszlása a hiperszférában. (Feltételezzük, hogy minden súlyvektor felhasználásra kerül sor, amely csak akkor folytatódik, ha a tömegeloszlás egyik megvitatott módját alkalmazzuk.)
A Grossberg réteg tanulás
A Grossberg réteg viszonylag könnyű megtanulni. A Kohonen réteg kimenetét bemeneti vektort a Grossberg neuron rétegbe táplálják, és a Grossberg réteg kimeneteit kiszámítják, a normál működéshez hasonlóan. Ezenkívül minden súlyt csak akkor korrigálunk, ha egy nemzero kimenettel rendelkező Kohonen-neuronhoz kapcsolódik. A súlykorrekció értéke arányos a Grossberg neuron tömegével és kívánt kimenetével, amelyhez kapcsolódik. Egy karakter rekordban
ahol ki - vyhodi- neuron Kohonen (csak egy neuron Kohonen eltér nullától); yj -j th a vektor komponense a kívánt kimenetek.
Kezdetben egyenlő
0,1, majd fokozatosan csökkenti a tanulási folyamatot.
Ez azt mutatja, hogy a súlya a Grossberg réteg konvergálnak az átlagértékek a kívánt kimenet, míg a súlyok a Kohonen réteg képzett a átlagértékei bemeneteket. A Grossberg-féle tanulás tanítása a tanárral, az algoritmusnak megvan a kívánt kimenete, amely szerint képzett. A tanár nélkül való tanulás, a Kohonen önszerveződő rétege nondeterminisztikus pozíciókban ad el. A Grossberg réteghez a kívánt kimenetekre vannak leképezve.
Az ellenzéki hálózat teljesen
Az 1. ábrán. A 4.4. Ábrán az ellevágó hálózat egésze látható. Normál üzemmódban bemutatják az X és Y bemeneti vektorokat, és a képzett hálózat az X 'és Y' vektorokat adja ki a kimeneten. amelyek közelítőleg X és Y értékek. Az X és Y vektorokat itt normalizált egységvektorokként feltételezzük, ezért a kimeneten generált vektorok szintén normalizálódnak.
A tanulási folyamatban az X és az Y vektorokat egyszerre tápláljuk bemeneti hálózati vektorokként és kívánt kimeneti jelekként. A VectorX a kimenetek megtanulására szolgál. és az Y vektort a Grossberg réteg Y 'kimenetének megtanulására. Az elosztóhálózatot teljesen felkészítették a közvetlen cselekvési hálózatban leírt módszerrel. Kohonen neuronjai elfogadják a bemeneti jeleket vektorokként. és vektorokból. Ez azonban nem különböztethető meg attól a helyzettől, amikor az X és Y vektorokból egy nagy vektor van. és nem befolyásolja a tanulási algoritmust.
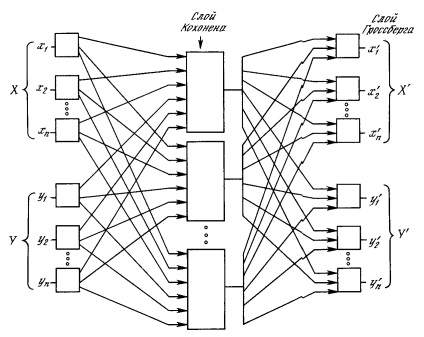
Ábra. 4.4. Teljes ellenkereső hálózat
Ennek eredményeképpen egyetlen leképezést kapunk, amelyben egy pár bemeneti vektor prezentálása a kimeneten a példányokat generálja. Ez nem különösebben érdekes, ha nem veszik észre, hogy csak az X vektor (az Y vektorral egyenlő nulla) bemutatása mindkét kimenetet X 'generálja. és kimenetek Y '. Ha F egy függvény X-re Y-ben. akkor a hálózat közelíti hozzá. Továbbá, ha F invertálható, akkor csak az Y (nullához igazodó) vektor bemutatása generálja X '-et. A függvény és az inverz egyedi létrehozásának képessége számos alkalmazásban hasznos lehet az ellenszaporítási hálózat számára.
Ábra. 4.4 a kezdeti konfigurációtól eltérően [5] nem mutat ellenáramot a hálózatban, amellyel megkapta a nevét. Ezt az űrlapot azért választják, mert a visszacsatolás nélküli hálózatot illusztrálja, és lehetővé teszi számunkra, hogy általánosíthassuk az előző fejezetekben kifejlesztett fogalmakat.