Éves parallaxis és a csillagok távolsága
Éves parallaxis és a csillagok távolsága

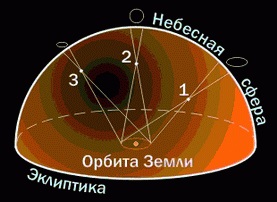
Gondolatok arról, hogy a csillagok távoli napok, még az ősi időkben is kifejeződtek. Hosszú ideig azonban nem világos, hogy milyen messze vannak a Földtől. Még Arisztotelész is megértette, hogy ha a Föld elmozdul, akkor figyelemmel kíséri a csillagok helyzetét a föld pályáján két átlós ponttól, akkor láthatjuk, hogy a csillag iránya megváltozik. A csillag látszólagos (parallactic) elmozdulása a távolság távolságaként szolgál: minél nagyobb ez, annál közelebb van a csillag. De nem csak Arisztotelész, hanem sokkal később Copernicus sem tudta felismerni ezt az elmozdulást. Csak a XIX. Század első felének végén. Amikor a teleszkópok pontos szögméréssel rendelkeznek, lehetséges volt egy ilyen elmozdulás mérése a legközelebbi csillagok közelében.
A p éves parallaxisa az a szög, amelynél a csillag csillagát a csillag pályájának merőleges tengelye (1 AU-nak felel meg) semimajor tengelye lehet.
Távolság a csillaghoz. D = a / sin (p)
ahol a a Föld pályájának szemimajor tengelye. A szinusz kis szögének a magának a sugárban kifejezett szögértékének a helyettesítésével, és a = 1 a feltételezésével. azaz a következő képletet kapjuk csillag csillagegységben lévő csillag távolságának kiszámításához:
A csillagokkal való távolságokra és fényességükre
1837-ben az éves parallaxis megbízható méréseit először végezték el. Orosz csillagász Friedrich Georg Wilhelm von Struve (1793-1864) töltött a méréseket a legfényesebb csillag az északi félteke Vega (a Lyrae). Szinte egy időben más országokban a parallaxisokat még két csillag határozta meg, amelyek közül az egyik a Centauri volt. Ez a csillag, amely nem látható Oroszországból, kiderült, hogy a legközelebb van hozzánk. Még hogy éves parallaxis csak 0,75.”Ilyen szögben látható szabad szemmel a drót vastagsága 1 mm távolságban 280 m. Ezért nem meglepő, hogy egy ilyen kis szögelfordulás mindaddig nem lehet figyelmen kívül hagyni.
A távolság a legközelebbi csillag, akinek parallaxis p = 0,75 „D = 206265” / 0,75 „= 270000 a. E. mértékegységeket távolságok olyan nagyok, és parsec fény évben.
Parsec - ez a távolság, amely a parallaxis A csillagok 1 „innen ered a neve a készülék: ... párok - a szó” parallaxis „a második - a szó” második „távolság parsecs egyenlő a kölcsönös éves parallaxis, például azért, mert a parallaxis alfa Centauri 0,75 ", a távolság 1,3 parsec.
A könnyű év az a távolság, amely a 300 000 km / s sebességgel terjedő fény áthalad az év során. A legközelebbi csillagtól a fény négy év alatt utazik a Földre, míg a Napról nyolc perc, a Holdról pedig egy kicsit több mint egy másodperc. 1 pc (parsec) = 3,26 fényév = 206 265 a. e = 3 • 10 ^ 13 km. Jelenleg a "Gipparcos" speciális műholdat használva több mint 118 ezer csillag éves parallaxisát 0,001 "-os pontossággal mértük.


Így most az éves parallaxis mérésével, 1000 ponttal vagy 3000 sv. év. A távoli csillagok távolságát más módszerek határozzák meg. Miután a csillagászok meg tudták határozni a csillagok távolságait, azt találták, hogy a csillagok ugyanolyan távolságban különböznek a látszólagos fényességben. Nyilvánvalóvá vált, hogy a csillagok különböző fényerejűek. A nap úgy tűnik, hogy a legfényesebb tárgy az égen csak azért, mert sokkal közelebb áll az összes többi csillaghoz. A fényerő az a teljes energia, amelyet egy csillag egységnyi idő alatt sugároz. Ez abszolút mértékegységekben (wattokban) vagy a napsugárzás mértékegységeiben fejeződik be. A csillagászatban gyakori a csillagok összehasonlítása a fényesség függvényében, kiszámítva látszólagos fényerejét (stellar magnitúdóját) ugyanazon szabvány távolságonként - 10 pc. Látszólagos nagyságrendű, hogy a csillag volna, ha ez volt a parttól távol D0 = 10 db, úgynevezett abszolút nagyságrendje M. Tekintsük hogyan kell meghatározni az abszolút nagyságát M, tudva a távolságot a csillag D (vagy parallaxis - p) és Emlékezzünk arra, hogy két forrás fényereje, amelynek csillagteljesítménye egyenként különbözik, 2,512-szer különbözik egymástól. Azoknál a csillagoknál, amelyek nagysága megegyezik az m1 és a m2 értékekkel, az I1 és I2 fényességük arányát a reláció:
Az ugyanazon csillag látszólagos és abszolút csillagmagasságai esetén a fényerő aránya így fog kinézni:
ahol I0 ennek a csillagnak a fényessége, ha távolról van D0 = 10 pc.
Ugyanakkor ismert, hogy egy csillag látszólagos fényereje fordítottan változik a távolság négyzetével. ezért
I. I0 = D ^ 2 0. D ^ 2 Ezért,
2,512M-m = D ^ 2 0D ^ 2. Ennek a kifejezésnek a logaritmusa megtalálható
0,4 (M-m) = lg 10 ^ 2-lgD ^ 2, vagy
M = m + 5 - 5 lg D, vagy
A Nap abszolút nagysága Mo = 5m. Más szóval, 10 cm-es távolságból a Nap úgy néz ki, mint az ötödik nagyságú csillag.
A csillag M abszolút csillagméretének ismeretében könnyű kiszámítani a fényességét L. A Lo = 1 napsugárzást feltételezve:
L = 2,512 ^ 5-M, vagy Ig L = 0,4 (5-M).

A fényesség (sugárzási teljesítmény) szerint a csillagok jelentősen eltérnek egymástól: egyesek sugárzik az energiát több millió alkalommal a Napnál, mások - több százezer alkalommal kevesebbet. A abszolút értékeit a legmagasabb luminozitás csillagok (óriások és supergiants) eléri M = -9m, és törpék a legalacsonyabb fényesség abszolút nagysága M = + 17m.