2. fejezet Adattípusok és hogyan kell dolgozni velük
Adattípusok és hogyan kell dolgozni velük
A számítógépes matematikai rendszerek, mint bármely más szoftver, adatokkal dolgoznak és feldolgozzák azokat. Mivel az SCM különféle jellegű dokumentumok készítésére összpontosít (beleértve az elektronikus dokumentumokat és könyveket is), széles körű lehetséges adatfajtákkal és azokkal együttműködő eszközökkel rendelkeznek. Ebben a fejezetben figyelembe vesszük a Maple 9.5 / 10 rendszerek adattípusait és azok kezelését.
Alphabet Maple-nyelv (a bemeneti és programozás) tartalmaz 26 kis karakter (A-Z), 26 nagy betűkkel (A-tól Z-ig), 10 arab számokkal (0-9), és 32 speciális karakterek (számtani műveletekkel: +, -, *, /, építési jel fok ^, stb) .. Emellett sok speciális matematikai szimbólum létezik. Mindegyiküket ebben a fejezetben ismertetjük. A karakterek bevitelét a billentyűzet és a matematikai szimbólumok.
Öt pár alternatív szimbólum van (ami ugyanazt jelenti):
A nyelv szintaxisának következő elemei a speciális egyedi és összetett karakterek szempontjából relevánsak:
•% - az előző művelet eredményét tároló rendszerváltozó;
•. - Expressz zár, amely megakadályozza, hogy a számítás kimenete a kimeneti cellába kerüljön;
•; - Expressz szorító, amely a számítási eredmény kimenetét adja ki a kimeneti cellának;
• `- karakterlánc-határoló (pl.` String `);
•: = - Hozzárendelési operátor (például x: = 5);
•. - változó típusú mutató (pl. n :: egész vagy z :: komplex);
• \ - a fordított osztás jele, amely többféle értéket tartalmaz a kontextustól függően (lásd a súgót ehhez a jelhez - backslash).
A fenntartott szavakat feltételes kifejezések, hurkok, eljárások és vezérlési parancsok létrehozására használják. A Maple rendszerben található fenntartott szavak listája az alábbiakban található.
és Break by Catch leírás
csináld Elif Else véget
hiba Export fi Végül a
a Globális, ha egymásba metszenek
legközelebb a helyi Minus mod modult
nem Od opció opciók vagy
proc Lekérd olvassa el a mentés vissza
hagyja abba, hogy megpróbálja az uniót
Ezek a szavak nem nevezhetők felhasználói objektumoknak.
Az a szabálykészlet, amellyel az összes Maple-nyelvű objektum definícióját írjuk, a szintaxisának nevezzük. A szintaxis egyes jellemzői hasznosak már a Maple fejlődés kezdetén. Például a jel - (mínusz) kettős jelentéssel bír. Egyetlen számra, változóra vagy kifejezésre alkalmazva megváltoztatja jelét. Azonban két mínusz jel egy sorban (például rekord3) nem adható meg. A mínusz jel másik célja egy kivonási művelet létrehozása, például 5-2 vagy a-b. Ennek megfelelően a kettős hozzárendelésnek van a + jele, és az alá nem írt számot pozitívnak tekintjük, tehát + 5 = 5.
Amikor valódi számokat ad meg a sorrend jelzésére, használja a ^ szimbólumot (például 2 * 10 ^ 100 vagy 2 * 10 ^ -100). Ha egy számot fel szeretnénk venni a hatalomra, a ^ kezelővel együtt használhatjuk az összetett operátort ** (két csillag egy sorban). A zárójelet a számítások általánosan elfogadott prioritásának megváltoztatására használják, és a funkciók és eljárások paraméterei is be vannak állítva. A Maple nyelv szintaxisát az alábbiakban részletesebben tárgyaljuk.
Néhány operátort két szimbólum képvisel: például az operátor értékeit változókhoz rendelve: = kettőspontot és egyenlő jelet tartalmaz. Ilyen kijelentéseknél a karakterek között nem engedélyezett szóköz karakter. Azonban használható a kifejezések egyes részei között - így (a + b) / c egyenértékű (a + b) / c.
A Maple teljesen természetes munkát kínál egész számokkal. Különösen lehetséges egy szám jelének megváltoztatása, és alap számtani műveletek végrehajtása számokkal. Tekintettel a számtani műveletek jól ismert ismereteire, azok definícióját nem adjuk meg. Az egyszerű műveletek példáira korlátozzuk az alábbi számokat:
Az egészszámú műveletek eredményeit az általános esetben racionális számok képviselik. amelyek egész számok kapcsolódnak.
A számjegyek tizedespontjának különleges állapota van - ami azt jelzi, hogy bárhol a számban, beleértve a végén is, a számot ténylegesvé teszi, és a számítások átviteléhez valós számmal való munkamódot eredményez. Például:
.3600000000 10 -13
A tizedesvessző után a számjegyek száma a rendszerkörnyezeti változó értékének szabályozásával szabályozható. Számjegyek:
> Számok: = 10; exp (1.);
Számjegyek: = 102,718281828
> Számok: = 40: evalf (Pi);
Amint e példákból látható, a számok bevitele és kimenete a következő jellemzőkkel rendelkezik:
• a mantissza teljes részét elválasztja a tört részből, használja az elválasztási pontot;
• a nulla mantissza nem jelenik meg (a szám elindul egy elválasztó ponttal);
• A mantissza szétválasztódik a sorrendtől egy olyan térrel, amelyet szorzójelként kezelnek;
• a komplex számok képzeletbeli részét az I. képzeletbeli egység szimbólumával (a négyzetgyök -1) szaporítjuk;
• Ha lehetséges, a Maple egy számszerű eredményt jelenít meg egy pontos racionális szám formájában (két egész szám aránya).
A számokkal való együttműködéshez a Maple sok funkcióval rendelkezik. Ezeket a jövőben figyelembe fogják venni. A többfunkciós függvény használatával a Maple átalakíthatja a számokat különböző bázisokkal (2-ről 36-ra, beleértve a bináris és a hexadecimális értékeket is) a decimális számokba:
> konvertálás ("11001111", tizedes, bináris);
> konvertálás ("1AF.C", tizedes, hex);
> convert ("Maple", decimális, 36);
A szimbolikus számítások elvégzésének képessége miatt a Maple, hasonlóan a többi SKA-hoz, pontos aritmetikát valósít meg. Ez azt jelenti, hogy az eredmény tetszőleges számú pontos számmal érhető el. Mindazonáltal nem szabad megfeledkezni arról, hogy ideálisan pontos numerikus számítások csak az egész műveletek esetében végezhetők el, például az alábbiak szerint:
942594775983835942085162312448293674956231279470254376832 \ 788935341697759931622147650308786159180834691162349000 \ 3549599583369706302603264000000000000000000000000
Megjegyezzük, hogy az utolsó példában a pontosság hirtelen elveszett, mivel a 100.0 exponens lebegőpontos számként lett megadva. Ennek megfelelően az eredmény egy ilyen szám formájában volt. Az eredmény érvényes számjegyeinek számát a rendszer változó Digit (alapértelmezés szerint 10) határozza meg.
Íme néhány példa bizonyos funkciók pontos számítására (a mantissza 150 karakterével):
0,84147098480789650665250232163029899962256306079837106567 \ 275170999191040439123966894863974354305269585434903790 \ 7920674293259118920991898881193410327729
A Maple és a Mathematica rendszerek fejlesztői azt állítják, hogy elvileg a számítások egy lebegőponttal lehetségesek, és a mantissza akár egymillió pontos számjegye is lehet. Gyakorlatilag ilyen pontosság szinte soha nem szükséges, legalábbis a fizikusok és a mérnökök számára. Például az π számnak csak 39 pontos számjegye elegendő ahhoz, hogy kiszámítsa a teljes univerzum kerületét a hidrogénatom átmérőjén belül. Azonban az igazi matematikusok egy időben egyszerűen "megszállottnak" számították a π számot nagy pontossággal. Valaki, aki az egész életét erre töltötte. Ramanujan kiemelkedően hozzájárult az ilyen számításokhoz, akik 1916-ban algoritmusokat és képleteket javasoltak tetszőleges pontosságú számításhoz.
Az 1. ábrán. 2.1 A Ramanujan egyik legismertebb képletének egyik feladata. Már a képlet összegének első futamideje (k = 1) megadja a π szám értékét, ha a számítás hibája kevesebb, mint 3 # 8729; 10 -8. A növekvő k 1-gyel minden alkalommal a tényleges tizedesjegyek számát 8-kal, azaz százmillió alkalommal növeli! Elvileg ez a képlet akár egy milliárd vagy annál pontosabb jelet adhat a π számról!
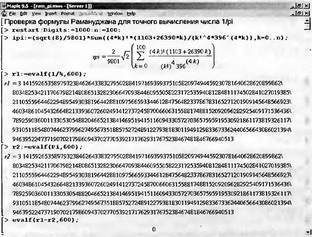
Ábra. 2.1. Számítások ellenőrzése Ramanujan-féle képlet szerint
A Ramanujan-képlet mérnökei fejfájás vagy fogfájás támadását okozhatják. Első látásra fájdalmasan kínos. Milyen pontossággal lehet mondani, ha a programozási nyelvek túlnyomó többségében a két, faktoriális és fokú négyzetgyök számítása csak 8-15 pontos jelzéssel történik?
A Maple 9.5 rendszerek azonban a beépített precíziós aritmetikai készülékeknek köszönhetően hatékonyan ellenőrizhetik az ilyen képleteket. Esetünkben az n = 100 esetre korlátoztuk (k maximális értékét), és a "csak" 600 számjegyű π számot számoltuk úgy, hogy az eredmények egy számra illeszkedjenek. És magukért beszélnek - a Ramanujan-képlet szerint számított számok és a beépített Maple-algoritmus szerint számított összes szám megegyezik, és a számított hiba nulla!
A juhar, természetesen, mint más SCM-k, komplex számmal dolgozhat z = Re (z) + I # 8729; Im (z) formában. A komplex számban lévő képzeletbeli egységet (a -1-es négyzetgyökét) I. jelöli. A Re (z) és Im (z) függvények visszatérnek a komplex számok valós és képzeletbeli részeihez. A komplex síkon a számokat a pontok koordinátáival adjuk meg (x, y) - Fig. 2.2.

Ábra. 2.2. Rendes és komplex számok reprezentálása a síkon
A számok ábrázolása a 2. ábrán. 2.2 A pontplot (lista) függvényt használjuk, ahol a lista a pontkoordináták listája. Ez a funkció akkor érhető el, ha a plotcs csomag kapcsolódik a parancshoz (diagramok). Ezenkívül a grafikus objektumok egy grafikus ábrázolásának funkciója jelenik meg (lásd az alábbi komplex számok ábrázolásának leírását).
Példák a komplex szám meghatározására és a valós és képzeletbeli részek származására:
A komplex számokat általában az úgynevezett komplex síkon ábrázolják, ahol az x koordinátát a komplex szám valós része határozza meg, és y (a képzeletbeli tengely) egy ilyen szám képzeletbeli részét mutatja. Az 1. ábrán. A 2.2. Ábrán a z = 4 + 3I, -z komplex számú sugárvektorok és a 4-3I komplex konjugátum száma látható. És az ábrán. A 2.3. Ábra egy példát mutat a z ^ n = 1 egyenlet gyökereinek kiszámítására az n = 16 esetnél (más esetekben az olvasó önállóan mérlegelheti, egyszerűen változtatva n). Látható, hogy az egyenlet gyökerei komplex számok, és a komplex síkon egy egység sugarú körön fekszenek.

Ábra. 2.3. A z ^ n = 1 egyenlet gyökereinek kiszámítása és a gyökerek helye a komplex síkon
A kör sugara az abszolút értéke egy komplex szám z = a + b * I. Ez egy geometriai készlet komplex számot, által alkotott forgó végét a sugár vektor Z körül elején pontban (0, 0) a komplex síkban, amint azt egy konkrét példa, és a szám . 2.2. Később megnézzük számos funkcióval rendelkezik komplex számok.
A számok bemenetként, kimenetként és konstansként szolgálhatnak a matematikai kifejezésekben. A függvénytípus (x, numerikus) lehetővé teszi annak megállapítását, hogy x egy szám. Ha így van, visszatér a Boolean true (true) értékhez, és ha nem, hamis (hamis). Például: