Nyílt profilú vékonyfalú rúd számítása

Az adott rúdhoz szükséges:

- meghatározza a súlypont helyzetét;

- kiszámítja a tehetetlenség fő központi momentumait;

- építsenek egy szektoriális területet (a pólust a szelvény súlypontjába helyezzük);

- számítsa ki a szektor-lineáris statikus pillanatot;

- meg kell alkotni a fő ágazati terület diagramját (tegye a pólust a kanyar közepére);

- a tehetetlenségi ágat kiszámításához;

- kiszámítja a tehetetlenségi nyomatékot tiszta torzítással;

- kiszámítja a hajlító-torziós jellemzőt;

- Írja le a csavarszögek és a határfeltételek differenciálegyenletét;

- kiszámítja a belső erőket a rúdon és hozzon létre a diagramokat (a rúd négy részre oszlik);

- Számítsd ki a normál feszültségeket egy veszélyes szakaszban és rajzolj rajzokat.

1. rendszersorozat; erő alkalmazásának 2 pontja;

1. Osszuk az ábrát protozoonra, határozzuk meg a négyszögek területét.

2. Határozza meg a szelvény súlypontjának helyzetét a tengelyekhez képest

3. Számítjuk ki a tehetetlenség fő központi momentumait

4. Számítjuk ki az ágazati területet.

A csatornát egy olyan tervezési sémával cseréljük ki, amely egybeesik a szakasz tengelyirányú vonalával. A z és y koordináták diagramjait állítjuk össze.

Az ágazati területdiagramot állítjuk össze (a pólust a P = C szakasz súlypontjában választjuk ki). 0 az ágazati terület eredete (a kontúr metszéspontjánál és a szimmetria tengelyénél).

hol vannak az elem kezdőpontjának koordinátái;

- az elem végpontjának koordinátái.

Koordináták 1 (4,04, 9)

2. pont (-9.46, 9)

a 3 (4,04, -9)

központ 4 (-9,46, -9)

gravitáció 0 (4,04, 0)

5. Határozza meg a kanyar közepének helyzetét.

Először kiszámítjuk a szektor-lineáris statikus pillanatokat, ehhez a diagramot a koordináták megfelelő diagramjaival (a Vereshchagin-módszer szerint) szorozzuk.

(a szimmetrikus diagram szaggatott szimmetrikus eredményének szorzata 0).

Meghatározzuk a hajlítóközpont pozícióit.

6. Hozza létre a fő szektorterület diagramját (tegye a pólust a P = D kanyar közepére). 0 az ágazati terület eredete (a kontúr metszéspontjánál és a szimmetria tengelyénél).

Koordináták 1 (-5,5; 9)

a 3 (-5,5, -9)

0 - a fő szektorbeli nullapont - a kanyar középpontjához legközelebb eső nulla pont, az egy szimmetriatengelyű szakaszokban a kontúr és a tengely metszéspontjában helyezkedik el.

7. Számítjuk ki a tehetetlenségi ágat.

Ehhez a grafikont ábrázoljuk. (a Vere-

Shchagin és Simpson képletét).

8. Számítsa ki a tehetetlenségi nyomatékot a tiszta torzióért

9. Számoljuk ki a hajlító-torziós karakterisztikát

Először kiszámítjuk a nyírási modulust:

10. A csavarszögek differenciál egyenlete

- a külső elosztott nyomatékterhelés intenzitása figyelembe véve a jelet (plusz jel, amikor a terhelés az x tengely pozitív irányából nézve az óramutató járásával ellentétes irányba forog)

Az önkényes állandók a határkörülményektől függenek

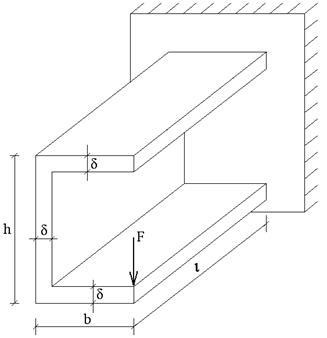
Megírjuk a határfeltételeket

A szabad vég ()

A rögzített vég ()

11. Számítsa ki a belső erőket. Számításokat számolunk egy táblázatban.

Nyomaték szabad torzítással

Torziós nyomaték torzítással

A rúdra ható koncentrált erő esetében minden szakaszban a következő feltételnek kell teljesülnie: