Hiperbolikus spirál, hiperbolikus spirál meghatározása, irodalomjegyzék - Archimedes spirál
Hiperbolikus spirál meghatározása
A hiperbolikus spirál egy sík transzcendens görbe, amelynek egyenlete a poláris koordinátákban a következő formában van:
A görbe két ágból áll, amelyek egyenes vonalhoz szimmetrikusak (lásd az ábrát). Az eredet aszimptotikus pont. Asymptote - egyenes vonal, amely párhuzamos a pólusos tengellyel és távoli távolságra.
Egy hiperbolikus spirált úgy kapunk, hogy egy pontot egy forgó vonal mentén mozgatunk oly módon, hogy a forgás középpontjától való távolság mindig fordítottan arányos legyen a vonal forgási szögétől a kezdeti pozíciótól mérve.
I. Megtaláljuk az ágazat területét:
A hiperbolikus spirál ívhosszát a következő képlet segítségével számítjuk ki:
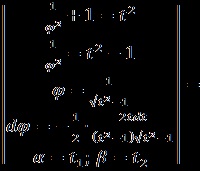
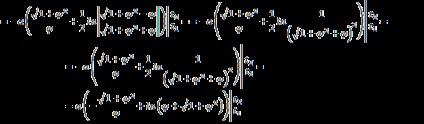
Így az M1 (,) és M2 (,) pontok közötti ívhossz az alábbi alakú:
1. A nagyméretű enciklopédikus szótár "Matematika"
4. Markushevich AI Csodálatos görbék, M. 1978
7. Fikhtengolts G.M. A differenciál és az integrál kalkulus folyamata; I. kötet, II-M. Nauka, 1969
9. A funkciók grafikái. Hivatkozási könyv. NA Virchenko Lyashko I.I. Shvetsov KI, 1979