Felmérés geodéziai munka egy topográfiai terv készítésében

ELLENŐRZÉSI MUNKA # 1 A "GEODESY"

VARIANTSCHIFR I (10) 56

Feladat1 Válaszok a "Geodéziai alapinformációk"

I. Információ a Föld ábrájáról. A geodéziában használt koordinátarendszerek. A vonalak tájolása.

Kérdés: Mit neveznek földrajzi vagy valódi azimutnak és irányszögnek? Mi az összefüggés egy adott vonal elülső és hátrafelé irányuló szöge között?

A terepvonal irányítása azt jelenti, hogy a meridiánhoz viszonyított irányát megtalálja. A vonalak irányát meghatározó szögek az azimuták, az irányszögek és a fodrok.

Azimut A jelentése a vízszintes szög számított óramutató járásával megegyező irányban igaz rész-ce, hogy egy előre meghatározott meridián irányban 0-tól 360 ° C (1. ábra) .Ha az azimut mérjük óramutató járásával megegyező irányban egy tényleges északi irány, hogy egy előre meghatározott meridián irányban 0-tól 360 °, akkor az ilyen azimuthot igaznak vagy földrajzinak nevezzük

A P1 P2 irányú azimutája (lásd az 1. ábrát) A1. és az azonos irányú inverz A2. A meridiánok nem párhuzamosak egymással, így a vonal azimutája minden ponton eltérő értékű. A két meridián irányának a két pont közötti irányát a meridiánok konvergenciájaként nevezik és jelölik # 947; Amint az 1. ábrából látható, a vonal előremenő és visszirányú azimutái közötti összefüggést a képlet adja meg

A referencia-szögek az Föld gömb alakú vagy gömbölyű felületén alkalmazhatók. Ha a földfelszínt bármelyik vetületben, pl. Gauss-Kruegerben, egy síkban ábrázolja, használjon sík referenciaszintet az irányszögnek.

A síkban lévő vonal irányszöge a tengelyirányú meridián és az adott irányban az óramutató járásával megegyező irányban 0 és 360 ° közötti kép közötti szög. Az irányszögeket egy betű jelöli # 945;

A 2. ábrából következik, hogy az azimutok és az irányszögek közötti összefüggést a képlet adja meg

ahol # 947 - a meridiánok konvergenciája a P1 pontban. azaz az axiális meridián és az adott pont meridiánja közötti szög között. Ha képletet kell venni, hogy a meridiánok konvergencia csekket, a megbeszélt kifolyjon a központi meridián, van egy plusz jelet, és lezárjuk a teendő - mínusz. Az ugyanazon vonal előremenő és irányított szöge 180 ° -kal különbözik, és meghatározzák:

Ha egy adott meridián és az axiális egy hosszúsága közötti különbséget jelöli, akkor a meridiánok konvergenciája a hosszúságok különbségével a hozzávetőleges képlet szerint

ahol B az adott pont geodetikus szélessége.

II. Általános információk a geodéziai mérések matematikai feldolgozásának méréseiről és elemeiről.

Kérdés: Mi a marginális hiba és hogyan határozzák meg?

A mérési hibák típusát, a geodéziás mérés osztályozását két szempontból vizsgálják: mennyiségi és minőségi, a mért mennyiség számszerű értéke és minőségi - pontosságának jellege. A gyakorlatból jól ismert, hogy a legmegbízhatóbb és pontosabb munkavégzés mellett sok többszörös mérés nem ugyanazt eredményezi. Ha az X mért mennyiség valós értékét jelöljük, és a delta mérés valós hibájából az l mérési eredményt a

Véletlenszerű hibák jellemzik a nyomkövetési tulajdonságokat. A mérési feltételek meghatározásakor a véletlenszerűek nem léphetik túl egy bizonyos határértéket, amelyet marginális hibának neveznek. Ez a tulajdonság lehetővé teszi a hiba észlelését és kizárását a mérési eredményekből. A pozitív és a negatív hibák egy sor mérésnél hasonlóan gyakoriak, ami segít a szisztematikus hibák azonosításában. Minél nagyobb a hiba abszolút nagysága, annál ritkábban találkozik számos dimenzióban. A számtani átlaga véletlenszerű mérési hibák az azonos nagyságrendű, az egyik végre feltételeket a korlátozatlan tumornövekedés az mérési hajlamos 0. Ez a tulajdonság kompenzációt. A véletlenszerű hibák utolsó tulajdonsága lehetővé teszi annak megállapítását, hogy az azonos nagyságú mérések sorozatából a legpontosabb értékhez legközelebb eső eredményt kapjunk. Ez az eredmény egy adott érték n mért értékeinek számtani átlaga. Végtelen számú mérések n lim (l | n) = X pontossága a végeredmény annál nagyobb minél nagyobb a n a helyes használata a mérési eredmények kell tudni bizonyos pontossággal - milyen mértékű közelség az igazi érték a mért érték, ők kaptak. Egy jellemző pontosság egyetlen mérési hiba elmélet javasolt Gauss négyzetes középhiba m, képlet alapján számítható ahol n száma a mérési értékek. Ez a képlet alkalmazható olyan esetekben, amikor a mért mennyiség valós értéke ismert. Az ilyen esetek ritkák a gyakorlatban. Ugyanakkor a mérésekből a valóságos értékhez - a számtani átlaghoz legközelebb eső eredményhez juthatunk. Átlagos négyzetes hiba podchityvaetsya képletű Bessel ahol - az eltérés az egyedi mért értékek Arif jelenti, az úgynevezett hiba valószínűsége. A középső aritmetika pontossága természetesen magasabb lesz, mint egy mérés pontossága.

III. Lineáris mérések

Kérdés: Mi a távolságmérés elve egy szálas keresővel? Írja be a munkamódszert.

Távolságmérési távolságok

Az ötlet alapul optikai távolságmérő határozat háromszög (egyenlő szárú vagy téglalap), amelyben a kis (parallaxis) szög p és a pro-tivolezhaschey ez Rhone-száz (alapon) határozza meg a távolságot-általános képletű D

Az egyik mennyiség (szög # 946; vagy a b) alapja állandó, a másik pedig mért. Ennek megfelelően állandó távolsági és változó alapú, állandó alapú és változó szögű távolságmérőket alkalmaznak.

Textil távolságmérő van távolságmérő yannym állandó szög és változó alapú, CO-torym szintező rúd függőlegesen beépített a vonalon-ce szegmens, amelynek hossza op redelyayut. Távolságmérő tartalmaz két vízszintes szálak párhuzamos az átlagos vízszintes izzószál mesh teleszkóp geodéziai eszköz (teodolit szintezés,) mérésére a távolság az egyik végét a szegmens korrigált eszközt a másik -. Mérőlécen.

EDM faktor általában egyenlő a 100, így távolságmérő olvasás a rúd santimet rah-expresszálják a kívánt távolság metrah.Dalnomernye izzóspirál rács kell elhelyezni egyenlő távolságra a középső vízszintes szál, hogy ellenőrizzük a különbség a példányszámot a rúd három audio-tyam: átlaga a számlák a szélsőséges fonalak kell esnie a cos átlagos száma a fonalat (mismatch referenciakeret-nek, hogy 3-4 mm).

A műszer útlevéladataitól függetlenül meg kell határozni a távolság-kereső arányt. Ehhez válassza ki a sík terep a vonal hossza mintegy 100 m, a kezdetektől a jelölési pont fölött, amely a közép-ruyut eszköz. Továbbá, az összehangolás vonal késlelteti a kiindulási pont értékét, a konstans tag C (egyenlő a belső cső FOCUS Coy, 0,1 m), és ebből a második pont, távolságméréshez egyenlő 20, 40, 60, 80 és 100 m. Azt határozzuk ezek a késleltetett távolságok a távolságmérőben kétszer, így a tartomány-távolság távolság a két meghatározás átlagaként.

Összehasonlítva a távolság-távolságot a ténylegesen mért értékekkel, kiszámítjuk a K együttható öt értékét, és a számtani középértéket vesszük a végértéknek.

A jelentős eltérés értékei KA-100 TSE célszerűségi (fölmérési), hogy ezt a hosszú távú intézkedés, hogy készítsen egy vasúti, amelyben a vasúti kell telepíteni a keményített címkézett előtt, a távolság 100 m, a vetítési jel rajta kezdve fonalak és osztott intervallum kapott (hagyományos mérő) 100 egyenlő részre. Ugyanaz a felosztás folytatódjon az alapozott lécek többi részén. A menetes távolságmérő távolságok meghatározására vonatkozó relatív hiba a mért távolság körülbelül 1: 300.

Mérési távmérő távolság két pont-kami elő intervallum hossza, on-eltérés, hogy a vízszintes szögben, ha a dőlésszög előnézet gyűrődések 1 ° 30”, az szükséges, hogy a megszámlált eredményt távolságmérő távolság a horizonton.

A távolság meghatározása menetes távolságmérővel a következőképpen alakul:

Ahol K a távolságmérő-együttható, és c állandó kifejezés.

A ferde távolságok mérésekor a vízszintes távolságot a következők határozzák meg:

v a teleszkóp látótengelyének dőlési szöge.

Kérdés: Mi a közvetlen és inverz geodéziai problémák lényege?

Közvetlen geodéziai probléma

A geodéziai problémák megoldásához a legmegfelelőbb rendszer a Gauss-Krueger vetület négyszög koordinátái. Ahhoz, hogy meghatározzuk a koordinátákat a későbbi pontok ismert koordinátáit a kiindulási pont, az ismert faji-pontok közötti távolságok és y-irányú ismert kristályok oldalán pontok közötti megoldott geodéziai vonal Env feladat.

Tegyük fel, hogy van egy A pontja az XA és az YA koordinátákkal. és a B 'pont koordinátáit X'B és Y'B jelöli (3. Húzzon rajta az A ponton az abszcisszal párhuzamos vonalat, és a B ponton keresztül az ordinát tengelyével párhuzamos vonalat. Ennek eredményeként egy téglalap alakú háromszöget kapunk, amelynek lába egyenlő a koordináták különbségével:

Az értékek # 916; x és # 916; y koordináta lépéseknek nevezik.

A jelentések ismerete # 916; x és # 916; y sides AB 'és a koordináták

az A kezdeti pontból, meghatározhatjuk a B véges pont koordinátáit,

Más szóval, a következő pont koordinátája megegyezik az előző pont koordinátájával és a megfelelő növekménygel, azaz általában:

A koordináta növekményének AB 'oldalának irányától függően # 916; x és # 916; y lehet plusz jel vagy mínusz jel. A koordináták növekményeinek jeleit az oldalsó irányok határozzák meg, azaz irányszögükön.

Az 1. ábrából. láthatjuk, hogy: # 916; x = dcos # 945; # 916; y = dsin # 945;

Figyelembe véve (4 # 916; x és # 916, a koordinátáknak nincs semmi több, mint az A és B pontok vízszintes távolságának d pontjai, és mások a koordináta tengelyen. A képletek egy közvetlen geodéziai probléma megoldására szolgálnak. A koordináta-növekmények jelei egybeesnek a trigonometrikus függvények jeleivel (ill. Az irányszög szinuszával és koszinusával).

A koordináta lépcsőzeteket háromféleképpen lehet kiszámítani: a trigonometrikus függvények természetes értékeinek táblázata alapján; a logaritmus táblázatokra és a koordináta növekményeinek kiszámítására szolgáló speciális táblázatokra, a használati szabályokról, amelyeket a táblázatokban szereplő magyarázatok tartalmaznak.

A gyakorlatban a felmérés az építési meghatározásához szükséges koordinátákat nem egyetlen ponton, mint a pontok sorozatát összekötött hori-tal Alkalmazások niyami helyszínek között és irányított szögek oldalai között megkötött ezeket a pontokat.

Fordított geodéziai probléma

Az építési gyakorlatban gyakran szükséges meghatározni az oldal hosszát és annak keresztirányát a végpontok ismert koordinátáitól, vagyis az inverz geodéziai probléma megoldásához. Ilyen feladat merül fel az építési tárgyak tervezése és áthelyezése a terepen.

Ha az ismert koordinátáit a két pont B „.. És egy (.. Ris4 cm), amelyről ismert, hogy növeljük a koordinátákat nem a Stora-AB”, akkor az érintő az irányszög AB oldal »eltökélt Thr-gon AB« B „:

A képletből tudunk írni:

D = √ (Xb'-Xa) 2 + (Yb'-Ya) 2 = √ # 916; x 2 + # 916; y 2

Az inverz geodéziai problémák megoldásakor ötértékű logaritmus táblákat használnak. Az irányszög nagyságának meghatározásához egy negyedet állítunk be a koordináták növekményeinek jelei szerint.

Kis számítógépek jelenlétében és jelentős számú probléma esetén ésszerűbb megoldani őket nem logaritmikus módon, a trigonometrikus függvények globális értékeinek ötértékű tábláit használva.

Feladat2 Problémamegoldás

1. feladat Határozza meg a BC és a LED vonalak irányszögeit, ha:

2. probléma Határozza meg az A pont téglalap alakú koordinátáit, ha:

X (C) = (- 14,02m) + (cos46gr41min 239,14m x) = (-14,02m) + (0,68949 x 239,14m) = 150,865m

V (C) = 627,98m + (sin46gr41minmin 239,14m x) = 627,98m + (239,14m 0,72429221172333114981112266078498 x) = 753,433m

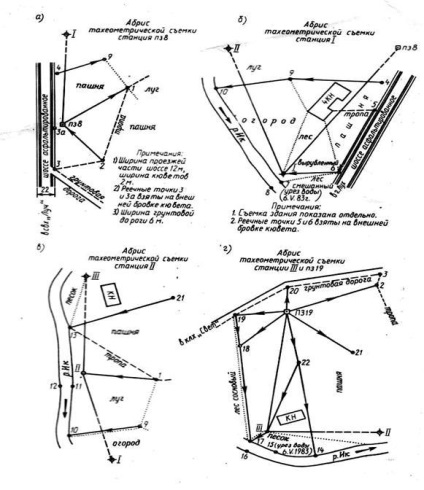
3. feladat: Az építési területre vonatkozó topográfiai terv készítése

A munka a következő szakaszokból áll: egy tachimetriás folyóirat feldolgozása; topográfiai terv készítése.

1. A terepen lévő helyszíni felméréshez a P38 és P319 két poligonometriai pont között egy teodolit-magassági pályát rendeltek. Ben minden oldal hosszát megmérik, és a stroke minden csúcsánál a jobb vízszintes szöget és a dőlésszöget

az előző és az azt követő csúcsokra.

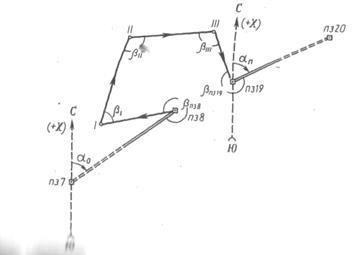
A vízszintes szögek és vonalak mérési eredményei (2. táblázat), valamint a trigonometrikus szintezés (4. és 4. táblázat) minden lehetőségre jellemzőek.

2. táblázat A löket oldalainak szögének és hosszának mérési eredményei

A PZ 8 és PZ 19 sokszög jelek (azaz a kurzus kezdő és végpontjai) koordinátái ismertek:

A kurzus oldalainak irányszögeinek és rázkódásának számítása. A kezdeti irányszög egy 0 és a korrigált értéket a szögek b löket szerint a képlet merőlegesen számított azimut összes többi felet: irányított szög oldala egyenlő a ezt követő irányított előző sarkában 180 ° plusz és mínusz jobb (korrigált) a stroke által bezárt szög ezen oldalán.

és PP 8-1 = a 0 + 180 ° - bPZ 8C = = 236 gramm 40,2 perc-189 gramm 59,2 perc = 46 gramm 41 perc

Az irányszög számításának vezérléséhez meg kell találni az utolsó irányszöget a az utolsó oldal III-PZ 19 végső szöge és a bPZ 19 korrigált szöge a PP 19 tetején

Ez a számított értéknek meg kell egyeznie a megadott irányszöggel. Ha az a szögeitől az r irányába mozog, akkor lásd az 1. táblázatot.

Az irányszögek értékeit az utasítás 4. oszlopában rögzítik egy tizedik perc pontossággal és az 5. oszlop rombuszai; míg a rhombák értéke egész percig kerekíthető.

A koordináta-lépések kiszámítása. A koordináta növekményeket az alábbi képletekkel számoljuk:

Dx = d cos a = ± d cos r; Dy = d sin a = ± d sin r

4. feladat Feladat megoldása az építkezés tervéhez

Task1 Határozza meg a vízszintes pontok közé eső pont jelét.

Nm.d (kisebb vízszintes vonal jelölése) = 185

a (kisebb vízszintes távolság) = x 20 =

S (a kontúrok közötti távolság) = m х 20 = m

Feladat2 A légi jármű meredeksége meghatározása