Bemutatás a matematikáról - mi a hiperbéles ingyenes letöltés









Mi túlzás? Túlzás megnyilvánuló emberi gondolkodás és a tudat primitív társadalomban. Sergeeva Evgeniya 8. osztályú diák
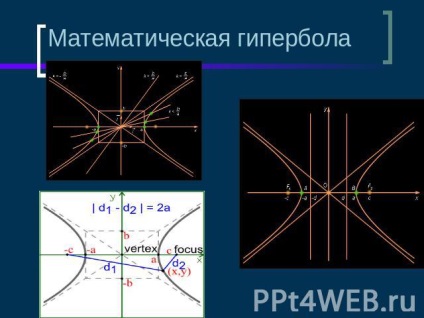
Származás giperbolyOdnim az első, aki elkezdte tanulmányozni a kúpszeletek - ellipszis, parabola, hiperbola, volt egy híres tanítványa Platón, az ókori görög matematikus Menaechmus (IV században.). A kocka megduplázódásának problémáját megoldva, Menechm tükrözte: "Mi történik, ha egy kúpot vágsz a generátrixára merőleges síkra?" Így, a változó az a szög, a csúcsa egy egyenes körkúp Menaechmus kapott három fajta görbék: Ellipse - Ha a csúcsszög a kúp akut; parabola - ha a szög egyenes; a hiperbola egyik ága - ha a szög elakad. Ezeknek a görbéknek a nevét nem találták fel Menechm. Ezek teszik lehetővé az egyik legnagyobb ókori geométerek Apollonius Virágpor, aki töltött egy csodálatos görbe értekezést nyolc könyvet „kúpszeletek” ( „On conics”). Hét könyv maradt fenn, közülük három - arab fordításban. Az első négy könyv tartalmazza az elmélet kezdetét és a kúpos szakaszok alapvető tulajdonságait. Ez - egy értekezést az ellipszis, parabola és a hiperbola, meghatározott szakaszai egy kör alakú kúp, ahol a bemutatót hozott a tanulmány evolutes kúpszelet. Apollonius megmutatta, hogy a görbéket úgy lehet elérni, hogy rajzolják ugyanazt a kör alakú kúp különböző részeit, és mindegyiket. A forgácsoló sík megfelelő lehajlásával minden típusú kúp alakú szelvényt el lehet érni. Ha feltételezzük, hogy a kúp nem végződik a csúcson, hanem rá van vetítve, akkor egyes szakaszokon két ág alakul ki.
A görbék leírása az algebra nyelvén egy matematikus választja a szelvény síkjában egy négyszögletes koordináta-rendszert, amelyben a görbék egyenlete a legegyszerűbb formában van. Ha az abszcissza tengelyt a kúpszimmetriasík tengelye mentén irányítja, és a görbére helyezi az eredetet. A név eredetét a következő ábra magyarázza. Minden téglalapot felépítünk a csúcson. Ehhez a függőleges görbét érintő négyzetet és az oldalt - a szimmetria tengelyét érintjük. Ezután a hiperbola-ban a tér négyzetese nagyobb, mint a téglalap.
Definíció Az inverz arányosság az y = k / x képlet által adott képlet, ahol k nem egyenlő 0-val. A k számot inverz arányossági együtthatónak nevezzük. Ha feltételezzük, hogy x egy független változó és y egy függő változó, akkor az y = k / x képlet meghatározza az y függvényét x függvényében. Az y = k / x függvény grafikonja hiperbola. A Hyperbola-nak két ágja van, amelyek az első és a harmadik négyzetben találhatók, ha k> 0, és a második és a negyedik negyedben, ha k> 0. Az y = k / x függvény. ahol k> 0 a következő tulajdonságokkal rendelkezik: a funkció tartomány - a készlet minden valós számok, kivéve a több 0mnozhestvo függvényértékeket minden szám, kivéve a 0 szám y = k / x - páratlan pozitívnak értékek x> 0 és negatív - ha x <0 убывает на промежутках х <0 и х> 0. Ha k <0, то функция y = k/x обладает свойствами 1—3, а свойства 4—5 формулируются так: принимает положительные значения при х <0 и отрицательные при х> 0 növekszik az x intervallumokban <0 и х> 0.
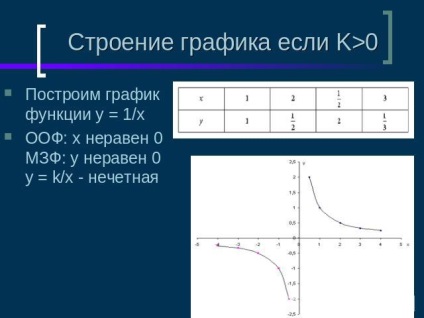
A grafikon struktúrája, ha K> 0A függvény grafikonja y = 1 / x OOF: x a 0MZF egyenlőtlenség: az egyenlőtlenségek esetén 0y = k / x - páratlan
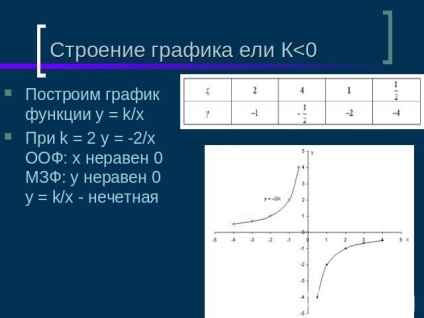
A fenyőfalak szerkezete<0Построим график функции y = k/x При k = 2 y = -2/xООФ: х неравен 0МЗФ: у неравен 0y = k/x - нечетная
Tehát megtudtuk, mi a hiperbola a matematikában.
Irodalmi hiperbola A hiperbola olyan figuratív kifejezés, amely egy tárgy vagy jelenség méretének, erősségének, jelentésének eltúlzott túlzásával jár. Például: "százötven nap alatt a nap lángolt" (Mayakovszkij). Használta a hiperboltot az érzelmi hatás fokozására az olvasó számára, és annak érdekében, hogy az ábrázolt jelenséget jobban ki lehessen emelni az egyik vagy a másik oldalon. Például: "És a véres testek hegye megzavarta a magokat" (M. Yu. Lermontov). Vagy NV Gogolban: "Sharovary, a Fekete-tenger szélessége"; - A száj a vezérkar ívének mérete. A hiperbola a szatíra legnagyobb szerepét játssza. A hyperbole lehet idealizálni és destruktív.
Következtetés: Az orosz nyelv magyarázó szókészlete, a hiperbola matematikai és stilisztikai gyakorlatok, mint szavak - amonímusok, de a fenti tények alapján elmondhatjuk a hiperbola fogalmainak hasonlóságát a matematikában és az irodalomban.