A vektor grafika matematikai alapjai
A SZÁMÍTÓGÉP GRAFIKAI TÍPUSAI
A számítógépes grafika az informatika területe, amely a szoftverek és a hardveres számítástechnikai rendszerek segítségével történő képalkotás és feldolgozás módszereit és eszközeit vizsgálja. A számítógépes grafika egyik legdinamikusabban fejlődő ága a számítástechnika és sok esetben működik, mint egy „mozdony” húz egy egész számítógép-ipar.
Alkalmazási területek:
- gyógyszer (számítógépes tomográfia);
- tudományos kutatás (az anyag szerkezetének vizualizálása, vektor mezők és egyéb adatok);
- textíliák és ruhák modellezése;
- fejlesztési fejlődés stb.
A képalkotás módjától függően a KG oszlik: bitképre, vektorra, fraktálra és 3D-re.
A pontokból álló raszterképek esetében különös jelentőséggel bír a felbontás fogalma, amely az egységnyi hosszúságú pontok számát fejezi ki. Meg kell különböztetni:
• a képernyőkép felbontása;
• A nyomtatott kép felbontása.
Eredeti felbontás. Az eredeti felbontása dózis per inch (dotsper inch - dpi) pontossággal mérve függ a képminőség és a fájlméret követelményeitől, a digitalizálás módjától vagy az eredeti illusztráció, a kiválasztott fájlformátum és egyéb paraméterek létrehozásának módjától. Általában a szabály érvényes: minél magasabb a minőségi követelmények, annál nagyobb az eredeti felbontása.
A képernyőkép felbontása. A kép képernyőn történő másolata esetén a raszter egy elemi pontját pixelnek nevezik. A képpont mérete a kiválasztott képernyőfelbontástól (szabványos tartománytól), az eredeti felbontástól és a kijelző méretétől függ.
Monitorok képalkotás 20-21 hüvelykes (szakmai osztály) általában egy szabványos képernyő felbontása 640x480, 800x600, 1024x768, 1280x1024, 1600x1200, 1600x1280, 1920x1200, 1920x1600 pixel. A foszfor szomszédos pontjai közötti távolság egy minőségi monitoron 0,22-0,25 mm.
A nyomtatott kép felbontása és a vonal fogalma. Dot méretű bitkép egy nyomtatott (papír, film és hasonlók. D.), és a képernyő függ az alkalmazott módszert és a paramétereket az eredeti szűrés. Raszterezéskor az eredeti egy vonalhálóval van ellátva, amelynek cellái raszteres elemet alkotnak. A raszterhálózat frekvenciáját az egy hüvelykre eső vonalak számával mérjük, és a lineáris értéknek nevezzük.
Raszterképek skálázása. A rasztergrafika egyik hátránya az úgynevezett pixelizálás, ha kibővített (kivéve, ha különleges intézkedéseket teszünk). Amint az eredetiben van egy bizonyos számú pont, majd nagyobb méretben, méretük is megnövekszik, a raszter elemei észrevehetővé válnak, ami torzítja az ábrát (1. A pixelizáció ellensúlyozása érdekében szokásos az eredeti digitalizálása előre, a felbontásnál a kiváló minőségű megjelenítéshez elegendő felbontással.
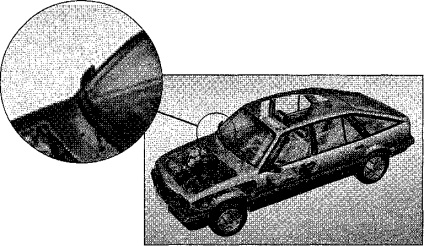
Ábra. 1. A pixelizálás hatása bitképes kép méretezésénél
Ha a rasztergrafika esetében a kép alapeleme egy pont, akkor a vektoros ábrán egy vonal van. A vonal matematikailag egyetlen objektumként íródott le, ezért az adatmennyiség, amely az objektumot vektoros grafika használatával jeleníti meg, lényegesen kisebb, mint a raszteres grafika esetében.
A vonal a vektoros grafika elemi objektuma. Mint minden tárgy, a vonal a következő tulajdonságokkal rendelkezik: formája (egyenes), vastagsága, színe, betűtípus stílus (szilárd, pontozott). A lezárt vonalak megszerzik a töltési tulajdonságot. Az általuk lefedett terület más tárgyakkal vagy egy kiválasztott színnel tölthető.
A legegyszerűbb, nem zárt vonalat két pont határolja, úgynevezett csomópontok. A csomópontok olyan tulajdonságokkal is rendelkeznek, amelyek paraméterei befolyásolják a vonal végének alakját és a felület más objektumokkal való jellegét.
A vektoros grafika többi objektuma sorokból áll. Például egy kocka hat összekapcsolt téglalapból állhat, amelyek mindegyikét négy összekapcsolt vonal képezi. Elképzelhető egy kocka és tizenkét összekötött vonal, amely bordákat képez.
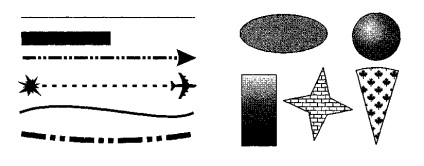
Ábra. 2. Vektoros grafikus objektumok
A vektor grafika matematikai alapjai
Vizsgáljuk meg részletesebben a különböző objektumok vektor grafikonban való ábrázolásának módszereit.
Pont. Ezt a síkban lévő objektumot két szám (x, y) jelöli, amely jelzi az eredeti helyzethez viszonyított helyzetét.
Egyenes vonal. Ez megfelel az y = kx + b egyenletnek. A k és b paraméterek meghatározásával mindig egy végtelen egyenes vonalat jeleníthet meg egy ismert koordináta-rendszerben, vagyis két paraméter elegendő egy sor meghatározásához.
A szegmens egyenes. Ez abban különbözik, hogy két további paramétert ír le - például a szegmens kezdetének és végének xl és x2 koordinátáit.
A másodrendű görbe. Ez az osztály a görbe parabola, ellipszis, kör, azaz az összes sort tartalmazó egyenletek mértéke nagyobb, mint a második. A másodrendű görbe nem tartalmaz inflexiós pontokat. Az egyenes vonalak csak a másodrendű görbék különleges esetei. A második rend görbének képlete általános formában például:
Így a másodrendű végtelen görbe leírása öt paraméter elegendő. Ha egy görbe szegmensét meg szeretné építeni, még két paraméterre van szüksége.
A görbe a harmadik rend. E görbék és a másodrendű görbék közötti különbség az inflexiós pont esetleges jelenléte. Például az y = x függvény grafikonja? van egy inflexiós pont az eredetre (15.5. ábra). Ez a funkció lehetővé teszi, hogy a harmadikrendű görbék alapul szolgáljanak a természetes objektumok vektoros grafika leképezéséhez. Például az emberi test hajlítási vonala nagyon közel áll a harmadik rendhez. Minden másodrendű görbe, mint a közvetlen, a harmadikrendű görbék különleges esetei.
Általános esetben a harmadikrendű görbe egyenlete a következőképpen írható le:
Így a harmadrendű görbét kilenc paraméter írja le. A szegmensének leírása további két paramétert igényel.
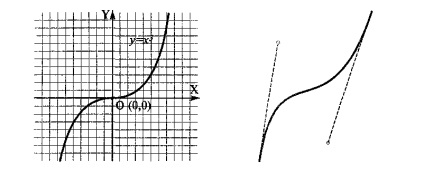
Ábra. 3. Harmadik rendű görbe (balra) és Bezier-görbe (jobbra)
Bezier görbék. Ez egy speciális, egyszerűsített harmadikrendű görbék. A Bezier-görbe megépítésének módja a vonalszakaszon rajzolt érintőpár használatán alapul. A Bezier-görbék szegmenseit nyolc paraméter írja le, így kényelmesebb a velük való együttműködés. A vonal alakját az érintő dőlésszöge és a szegmens hossza befolyásolja. Így a tangensek a virtuális "karok" szerepét játszhatják, amelyen keresztül a görbét szabályozzák.