A gerendák helyi és általános stabilitása
A gerendák általános stabilitásának biztonságát a következő képlet igazolja:
ahol a Wc az öv legkompresszáltabb szálak ellenállásának pillanata a legnagyobb hajlítónyomaték síkjában;
jb egy olyan együttható, amely figyelembe veszi a tervezési feszültségek csökkenését az általános stabilitás gerincének elvesztésével, amelyet az app. 7 SNiP II-23-81 *;
Ha a vizsgálat eredményeként az általános stabilitás nem biztosított, növelni kell a szalag szélességét vagy vízszintes összekötéseket kell létrehozni.
A gerenda stabilitásának ellenőrzése az alábbi esetekben nem szükséges:
1. terhelés áthelyezése szilárd kemény merevlemezen keresztül, folyamatosan támaszkodva egy sűrített merevítőszalaggal;
2. A Lef számított hossza és a bf szélesség közötti arány, amely nem haladja meg a II-23-81 * SNiP-ben meghatározott értékeket.
A gerenda falának stabilitása
A stabilitásvesztés kritikus normál, tangenciális vagy helyi feszültségekből eredhet, amelyeket a következő képletek határozhatnak meg:
- kritikus normál feszültségek
- kritikus tangenciális feszültségek
- kritikus helyi stresszeket
A Ccr a táblázatból vett együttható. 21 SNIPII-23-81;
d a lemez kisebb oldalai;
a a keresztirányú merevítők tengelyei közötti távolság;
m a lemez nagyobb oldalának a kisebbhez viszonyított aránya;
С1 - a táblázat együtthatója. 23 II-23-81. SNIP;
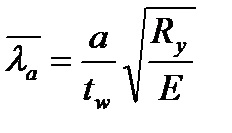
tw = t a falvastagság.
A rekeszfal feltételes rugalmassága
A fal feltételes csökkentett rugalmassága
A helyi stabilitás ellenőrzése csökkenti az ellenőrzési feltételeket:
- normál feszültségek hatására s £ scr;
- tangenciális feszültségek hatására t e tc;
- a helyi stresszek sloš £ sloc, cr
Az s, t és sloc hangsúlyozza:
- És ha ti - ha hw> a a hw / 2 szakaszban a széltől (ahol a hajlítónyomaték nagyobb) A tangenciális feszültségeket a gerenda falának átlagos keresztmetszeti területeként határozzák meg, anélkül, hogy figyelembe vették volna az övek munkáját a következő képlet szerint: ahol Q a keresztirányú erő a gerenda számított szakaszában. A szokásos igénybevételeket a falon a következő képlet alapján határozzák meg: A koncentrált terhelés helyi feszültsége: ahol P a koncentrált terhelés; tw a falvastagság; Lef = b + 2tf a koncentrált terhelés nyomáseloszlásának feltételes hossza.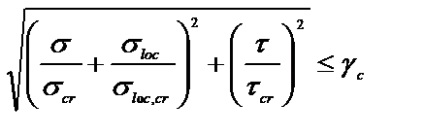
ahol gc a működési feltétel együtthatója;
s, t, sloc a tényleges stresszek a vizsgált ponton;
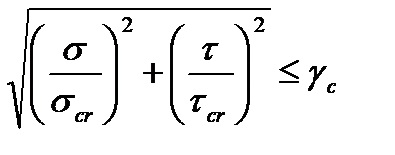
A sloc = 0 esetén a fal helyi stabilitását a következő képlet igazolja:
A gerenda falát nem szabad megerősíteni keresztirányú merevítőkkel, ha a feltételes rugalmasság értéke.
(mobil terhelés hiányában);
és (ha a gerenda övén mozgatható terhelés van)
A keresztirányú élek közötti távolság nem haladhatja meg:
A pár szimmetrikus élének nyúlványának szélességét feltételezzük, hogy egyenlő:
A gerendák falainak helyi stabilitását nem szükséges ellenőrizni. Ha a fal feltételes rugalmassága nem haladja meg az értékeket:
- helyi feszültségek hiányában (sloc = 0) a kétoldalas derekas varratok gerendáiban;
- ha vannak helyi feszültségek (0-as sloc).
42. A gerendák támogatása és összekapcsolása.
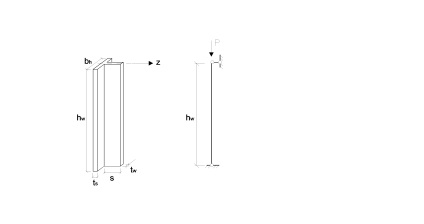
A merevítő borda méretét a borda szélének kiszámításával határozzuk meg:
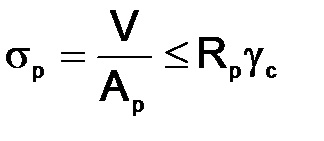
ahol V a referenciasugaras szakasz;
Ar - a támasztó borda zúzásának területe;
Rp - az acél szerkezeti ellenállása a táblázathoz való összetöréshez. 1 SNIP II-23-81 *
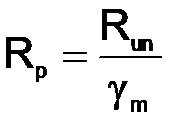
ahol gm a táblázat szerinti anyag megbízhatósági együtthatója. 2 SNiP II-23-81 *;
Futás - az acél standard ellenállása, a táblázatban foglaltak szerint. 51 SNIP II-23-81 *.
Szükséges terület a támasztó borda fenekének zúzására
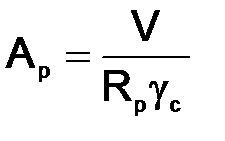
Miután definiáltuk Ap-et, megszerkesztjük az él keresztmetszetét (ts és bh meghatározása).
A ts (16, 20 mm) beállítása megmutatja a szél szélességét
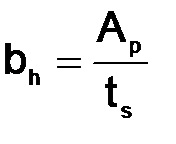
A borda kiálló részének szélessége a helyi stabilitás állapotától nem haladhatja meg
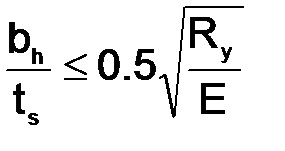
A támasztó borda kinyúló része nem haladhatja meg a 1,5 font értéket, és általában 15,20 mm-re van.
A gerenda tartóelemét stabilizálja a gerenda síkjából a következő képlet szerint:
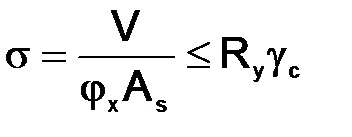
Amint az a hordozóoszlop hagyományos keresztmetszeti területe, amely magában foglalja a támasztó borda keresztmetszetét és a falszalag szélességét a borda mindkét oldalán
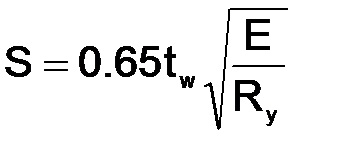
jx a hagyományos tartóoszlop keresztmetszetének hosszanti hajlítási együtthatója a Z tengelyhez viszonyítva, a táblázat szerint. 72 SNIP II-23-81 * állapotot, azzal a feltétellel, hogy a megerősítő borda és a fal árnyékolt része magassága hw.
A támasztó borda rugalmassága
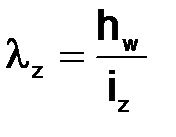
ahol iz a merevítő borda tehetetlenségi sugara és a fal árnyékolt része a Z tengelyhez viszonyítva.
44. Központilag tömörített oszlopok. Általános jellemző.
A központilag tömörített oszlopok bevonatok, fedvények, munkaállványok, stb.
Az oszlop három fő részből áll:
Az oszlop szakasza szerint. szilárd és átmenő.
A központilag tömörített oszlopok tervezésénél biztosítani kell az oszlop stabilitását a szekció fő tengelyeihez képest.
Rakományok oszlopainak racionális szerkezete:
- legfeljebb 2700 kN-ig használhatók szilárd oszlopok;
- 2700 és 3500 kN között kétcsatornás oszlopokon keresztül;
- 5000-től 6000 kH-ig két I-gerenda oszlopai között;
- több mint 6000 kN, az összetett hegesztett szakaszok oszlopait használják.
A rugalmasság kialakításához szükséges oszlop becsült hossza: # 956; l,
ahol én az oszlop hossza; # 956; - a tervezési hosszúság együtthatója, az oszlop rögzítési módjától függően.
# 956; = 1 # 956; = 0,7 # 956; = 0,5 # 956; = 2 # 956; = 1
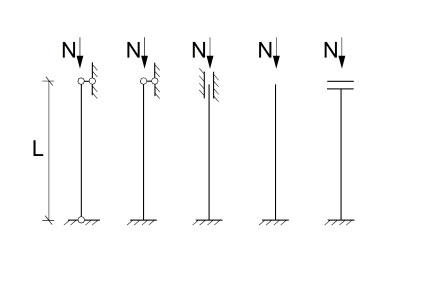
45. Folyamatos, központilag tömörített oszlopok. A szakasz kiválasztása.
A szilárd oszlopok kiválasztását a következő sorrendben végezzük:
1) válassza ki az oszlop típusát (ha nincs megadva) és annak tervezési sémája;
2) határozza meg az oszlop szükséges keresztmetszetét:
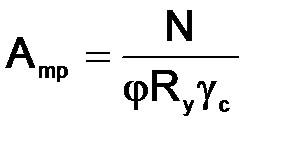
Az oszlop rugalmasságának meghatározása a terhelés függvényében (L = 6,7 m) a táblázat alapján határozható meg. 72 SNiP II-23-81 * hosszirányú hajlítási együttható j;