Miért repül egy repülőgép, vagy a tömeg és a lendület áramlik
az ismert S. Nuke amerikai csillagász (1835-1909) matematikailag bizonyította, hogy lehetetlen a levegőnél nehezebb légi járművek létrehozása.
Ha kérdezel egy járókelőtől, hogy miért repül a gép, akkor válaszol: az égen (miért). És rossz lesz - ahogy látni fogjuk, a gép repül ... a földön!
Először is, emlékezzünk egy jól ismert problémára. A mérlegen két áttetsző doboz van. Az egyikben egy légy ül, egy másikban - ugyanazon fly legyek. Mit mutatnak a mérlegek? A válasz nulla. Mert egy repülő repülő, hogy a levegőben maradjon, egy lendületet hoz létre, amely pontosan megegyezik a súlyával. Ez a lendületes irány (májgyengeség), amelyet lefelé irányítanak, átkerül a doboz aljára, egyensúlyba hozva a légyet a másik dobozban.
Talán nem mindenki tudja, mi a lendülete? Vegyünk egy másik példát.
A helikopter úgy néz ki, mint egy helikopter a levegőben. Mi megengedi neki, hogy ne essen? A csavar "szar" a pihentetett levegő ("a végtelenben") nyugalmi állapotban van (v ∞ = 0) = 0 \ jobb)>. és v sebességgel dobja le. Természetesen ez a levegő előbb-utóbb visszatér a helyére, így a helikopter egy toroidális örvényt hoz létre, összekeverve az egész légkört, amint az az 1. ábrán látható (minőségi szempontból).
Ha a levegő sűrűségét ρ kg / m³ értéken jelezzük (és szubszonikus sebességeknél az áramlás sűrűsége állandónak tekinthető), akkor az egységnyi idő alatt áramló levegő tömege a S sebességgel v. egyenlő: μ = ρ v S [kg / m³ ⋅ m / s ⋅ m² = kg / s].
Emlékezzünk erre a képletre. Áramlási sebesség Q [m³ / s] a folyadék vagy gáz térfogata az áramlás vagy a cső egységenkénti keresztmetszetén keresztül: Q = Δ V Δ t >>.
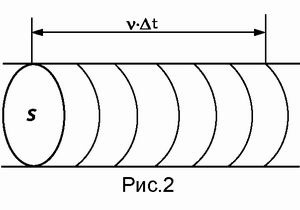
Legyen S az áramlás keresztmetszete, v sebessége. Ezután a ΔV = s ⋅ v ⋅Δt térfogat áthalad a Δ t időintervallumon keresztül a keresztmetszeten (2. ábra). Akkor Q = ΔV Δt = s ⋅ v> = s \ cdot v> és μ = ρ ⋅ Q = ρ ⋅ s ⋅ v. Ezt a mennyiséget természetesen tömegáramnak nevezhetjük. Ha pedig az áramlás keresztmetszetével osztjuk meg, akkor a tömegáram-sűrűséget μ S = ρ v> = \ rho v> [kg / (m² ⋅ s)
Te kérdezed, miért van itt a föld, és igazad van - NINCS ESEMÉNY.
Most döntse el a helikoptercsavar síkját "előre" (3. ábra)
Elbontjuk nyomóerő a függőleges komponense, és egy vízszintes Y X. A helikopter repül a erő irányában X, Y komponensnek természetesen, kell maradnia egyenlő súlyt, és X jelentése egyensúlyban ereje légellenállás. A síkban a két erõ létrehozásának szerepe meg van osztva: a szárny létrehoz egy függõleges (emelõ) erõt, és a motort - a húzóerõt. (Részletek a „hozzon létre egy függőleges szárny (emelés) erejét” - de hogyan?) És a szárny egy figyelemre méltó tulajdonsága: képes létrehozni egy emelő erő jóval nagyobb, mint az erő a légellenállás, hogy állásfoglalásra. A fizikus azt mondaná - nagyságrendje nagyobb. Ez természetesen nem jelenti azt, hogy "pontosan 10-szer nagyobb" - mind a 8, mind a 20 lehet. E két erõ arányát Y X = K> = K> szárny minõségnek nevezzük. Következésképpen, ellentétben helikopter szárnyas légi jármű szüksége van egy erő tolóerő a sorrendben súly a gép (és valójában még egy álló helikopter lebeg kell rendelkeznie felhajtóerő nem kisebb súly - és még inkább a horizontális elmozdulás).
Körülbelül fél évszázadon a repülőgépek a propeller propeller tolóerejét alkalmazták. A modern repülőgépek jet-motorokat használnak. De a fizikai elv ugyanaz: minden motornak lendületet kell adnia.
Mérjük meg, milyen sebességgel kell a gép motorját visszaszorítani a gáz tömegére. Ha a repülőgép tömege G, a szárny K minősége, és N motorokat fogunk használni, akkor mindegyiknek létre kell hoznia egy G / KN húzóerőt. Továbbá, ha a kimenet a motor-keresztmetszeti felület S gáz sűrűsége ρ s> kipufogógáz sebessége v, a tömeg fluxus egy koordináta-rendszerben a légi járművel kapcsolatos, μ = ρ sv S.> \ Rho _ >>>> [kg / s] . Feltételezzük, hogy az egyenlő a motor bejáratának tömegáramával. Ez azt jelenti, hogy figyelmen kívül hagyja a súlytöbblet az elégetett üzemanyag - a szerepe az utóbbi ezért ez jön le, hogy meleg a levegő, és nem növeli a tömegáramot - és kevésbé üzemanyag-fogyasztás, gazdaságosabb repülőgép-hajtómű. Ezután a motoron áthaladó levegő felmelegedésének eredményeképpen a sebesség (és ahogyan arra emlékeztetünk, az adott impulzus) nő a v-u-val, ahol u a repülési sebesség (4.
Így a mozgásmennyiség-változás (és ez az egyik tolóerő) jelentése F 1 = μ (VU) = ρ su S (VU) = G / K N. = \ mu (VU) = \ rho _uS ( vu) = G / KN.> Tegyük fel, hogy a motornyomásnál a gáznyomás pontosan megegyezik a környezeti levegőnyomással (index ∞), és hőmérsékletük Ts. Ezután a Mendeleev-Clapeyron-törvényből származik a sűrűség: ρ s = p ∞ / R T s. = P_ / RT _,> ahol R = R 0 / M / M> - gázállandó, R 0 = 8 31 = 8,31> J / K ⋅ mol, M = 29 ⋅ 10-3> kg / mol - moláris a levegő tömege. Egyébként figyelmet fordítunk arra, hogy az ρ s> kipufogógázok sűrűsége ne legyen egyenlő a légkör sűrűségével, amelyet az index s hangsúlyoz.
Számszerű becsléseket készítünk. Tekintsük a modern a repülőgép súlya G = 400 T = 4 ⋅ június 10 HH> amelynek N = 4 Motor r sugara a kimeneti szakaszán egy méter, repülő szubszonikus sebességgel u = 250 m / s magasságban több mint 10 km, a légköri nyomást ötször kisebb nyomást tengerszinten, p ∞ = 10 5/5 = 2 ⋅ 10 4 = 10 ^ / 5 = 2 \ cdot 10 ^> Pa. Mi az a Ts. Ezeket a számokat egyenletben helyettesítjük
F 1 = p ∞ / RT sv π r 2 (VU) = G / KN = 4 ⋅ 10 6 / (4 ⋅ 10) október 5 = H = P_ / RT_v \ pi r ^ (VU) = G / KN = 4 \ cdot 10 ^ / (10 \ cdot 4) = 10 ^ H>
Ennek a kvadratikus egyenletnek a megoldásával (v-rel szemben) v> 500 m / s találunk.
Természetesen egy ilyen motor (ahol a kimeneti szakasz sugara egy méteres sorrendben van) csak egy nagyon nagy transzatlanti béléshez tartozhat. De miért nyereséges nagy repülőgépek építésére? Ez megfelel a hasonlóság elméletének, amely Jonathan Swift idején is ismert volt. Itt azt írja erről a tanú Gulliver: „Matematika Őfelsége, hogy határozza meg a magasságot az én növekedés segítségével egy negyed, és megállapította, hogy ez a magasság ebben a tekintetben, hogy a magassága egy törpe, mint 12-1, kötött alapján a hasonlóság a testünk, hogy a kötet az én a test legalább 1728 Lilliputianus testének nagyságrendjével egyenlő, következésképpen annyiszor annyi ételt igényel. " Más szóval, ha a Lilliput egy szendvicsre támaszkodik, akkor Gulliver - 12½ szendvicset. Nyilvánvaló, hogy itt a Lilliput és a Gulliver testének azonos tömegsűrűségére vonatkozó feltevés készül.
Egy másik dolog - a repülőgép. Amint az (1) kifejezésből látható, az emelőerő arányos a térfogatnak, de a felszínnek. Tehát, ha a repülőgép jellegzetes méretét N-szer növeli, a térfogata N³-kal, a szárny területével, és ennek következtében a súlyával N²-kal nő. Ez azért van, mert a repülőgép héja, nem szilárd test. (Nyilvánvaló, hogy ezeknél az érveknél ρ v 2> - az úgynevezett sebességfej - feltételezik, hogy fix).
Igen, de! - a figyelmes olvasó felkiált: - miután minden formula (1) megkapta a helikoptert, és már beszélünk repülőgépekről? Itt meg kell nyugtatni a figyelmes olvasó ezekkel a szavakkal: Igazad van, de ha elfogadjuk, hogy a szél ható erő a repülőgép, sűrűségétől függően ρ [kg / m³], a sebesség v [m / c], és a méret L [m ], akkor ezeknek a mennyiségeknek az egyedüli kombinációja a következő: ρ v 2 L 2 L >> [kg / m³ ⋅ m² / s² ⋅ m2 = kg ⋅ m / s²]. Természetesen ennek az erőnek a numerikus értékének meghatározása érdekében figyelembe kellene vennünk a még ismeretlen dimenzió nélküli szorzót, de csak az erők kapcsolatáról érdekeltünk, nem pedig nagyságrendjükben.
Tehát, milyen magasságban nem repülne a repülőgép, egyszerűen köteles egy egyenlő súlyú impulzusáramot létrehozni, lefelé irányítva, és végül a földre hajolni.
De természetesen nem csak a legyek, a helikopterek és a repülőgépek. Az általunk figyelembe vett áramlások és áramlási sűrűség fogalmai gyakran találkoznak a fizika számos területén. Ezek nagyon hasznos fogalmak. Valószínűleg már sejtette, hogy megadhatja nemcsak a koncepció a tömegáram és a lendület, hanem más fizikai mennyiségek: az áramlás perdület (ha valami kiderül), az energia áramlását, az áramlás elektromos töltés (más néven áramerősség), indukciós áramlás egy mágneses mező ... de nem sok más, mi mást. De először elég mondtam.
Tehát ha közölné rokonokkal, barátokkal és ismerősökkel, hogy a sebesség egy konkrét impulzus, és az erő a lendület, akkor teljesen igaza lesz. És ha hozzáfűzi, hogy a nyomás az impulzus áramlásának sűrűsége, akkor nagyon okos lesz az iskolában, és biztosan belép a MIPT-be.
1. Becsülje meg az N μ T üzemanyag minimális áramlását (tömegáramlását), ami szükséges ahhoz, hogy biztosítsuk a légijárműnek a szövegben figyelembe vett vonóerejét. Egy kilogramm üzemanyag égetésekor az energia r, J / kg (fűtőérték) felszabadul. Vegyük úgy, hogy ezt az energiát az ellenállási erő (NF 1>) leküzdésére használják, és megváltoztatják a gázok kinetikus energiáját (a motorok előtt és után). A hőenergia elvesztése elhanyagolható. Kerozin esetében vegyen r = 40 MJ / kg.
2. Hasonlítsa össze az üzemanyag-fogyasztást a levegőfogyasztással.
3. Becsülje meg a szóban forgó repülőgép szárnyainak területét.