Geometriai értelmében a származék, matematika-ismétlés

Bejegyzések „geometriai jelentése a származék”

Levezetjük az egyenletet az érintő a grafikon y = f (x) a ponton az abszcissza x0. Az érthetőség kedvéért használjuk a grafikonon

10.3 Az előző leckében. ( „Meghatározása származék. Geometriai értelmében a származék”), és abból az egyenlet az érintő MT.

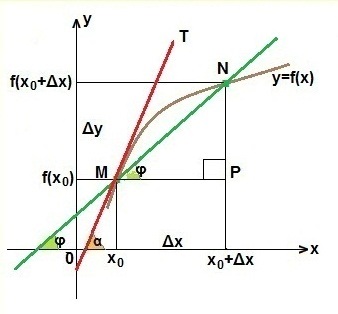
Mivel az M pont tettünk önkényesen, meg kell kap az egyenlet az érintő, hogy érvényes legyen minden olyan funkciót, y = f (x). amelynek érintője egy bizonyos ponton abszcissza x0.

Szóval, minden vonal lehet írott formában y = kx + b. ahol k - a görbe meredekségét. Ma már tudjuk, hogy mivel a lejtőn vehet f „(x0) - értéke függvény deriváltját y = f (x) a ponton a abszcissza x0. Ez pont egy olyan közös pont, hogy a funkció és az érintési MT.

Így, az érintő MT a következő alakú: y = f „(x0) · x + b. Továbbra is meghatározni az értékét b. Ez az, amit teszünk egyszerű: helyettesíti a pont koordinátáit M az utolsó egyenlet, tehát helyett x írunk x0. hanem a helyettesítő F (x0). Kapjuk egyenlőség:

A következő feladatok ellátására.

1. Írja az egyenletet az érintő a függvény grafikonját y = x 2 azon a ponton, x0 = 3. Tedd rajz.

Az egyenlet az érintő a grafikon y = f (x) x0 a abszcisszán az általános formája:

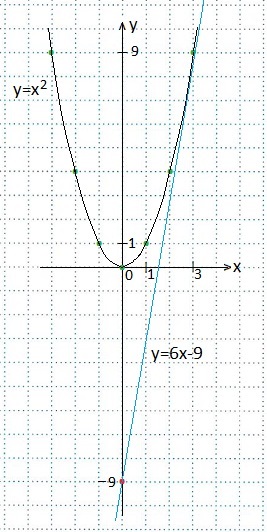
Keresse az értéke ennek a funkciónak egy adott abszcissza:

Azt találjuk, a származékot f '(x) = (x 2)' = 2x, és megtalálja az értéke ez a származék, ha X = 3.

Mi helyettesíti a mért értékeket

y = 6, x-9 - a kívánt egyenletet az érintő.

2. Írja az egyenletet az érintő a függvény grafikonját

Írunk általános egyenlete az érintő: y = f (x0) + f „(x0) (x-x0). Találunk az értéke ennek a funkciónak az x = 1. kapjuk:

f (x0) = f (1) = 1. Keressük a származékot ezt a funkciót, a levezetett fokozat:

Találunk az értéke ennek származéka, ha x = 1.

f „(x0) = f (1) = - 2 · (1) -2 = -3. Behelyettesítve a talált értékeket az általános egyenlet érintő:

A koordináta-síkban XY úgy a grafikon y = f (x). Fix egy M pont (x0, f (x0)). Adjunk az abszcissza x0 növekmény Ah. Kapunk egy új abszcissza x0 + Ah. Ez abszcisszán a pont N. és az ordináta megegyezik az f (X0 + Ah). Változás abszcissza változást eredményezett az ordináta. Ez a változás az úgynevezett növekmény funkció, és jelzik Δy.

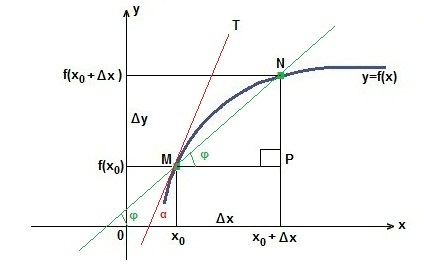
Δy = f (X0 + Ah) - f (x0). Keresztül az M és N pontok tartsa metsző MN. amely szöget zár be a pozitív iránya φ-tengely Ox. Mi határozza meg a szög tangense φ a derékszögű háromszög MPN.

Hagyja Ah nullához. Ezután a szelő MN törekedni fog arra, hogy elfoglalja a pozícióját érintő MT. és az a szög φ válik szöget α. Ennélfogva, a tangense szög α a korlátozó értéke tangens φ:

Meghatározása származék. Határa az arány a növekmény funkció a növekmény az érvelés, amikor az utóbbi nullához, az úgynevezett származékot egy függvény egy adott pontban:

A geometriai jelentése a származék az, hogy a számszerű származékot egy adott pontban megegyezik a szög tangense által alkotott húzott érintő ezen a ponton keresztül, hogy ez a görbe, és a pozitív irány Ox:

1 megtalálja a növekmény az érvelés és a növekmény a függvény az y = x 2 Ha a kiindulási érték az érvelés egyenlő 4, és az új -4,01.

Az új érték az érvelés x = x0 + Ax. Helyettesítő adatok: 4,01 + H = 4, így az érv növekmény AH = 4,01-4 = 0,01. Növekmény funkciót, definíció szerint, egyenlő a különbség az új és a korábbi függvény értékei, azaz Δy = f (X0 + Ah) - f (x0). Mivel van egy függvény az y = x 2 a Au = (X0 + Ax) 2 - (x0) 2 = (x0) 2 + 2x0 · Ax + (Ax) 2 - (x0) 2 = 2x0 · Ax + (Ax) 2 =

Lehetséges volt, hogy megtalálják a növekmény eltérően működnek: Δy = y (X0 + Ax) -y (X0) = y (4,01) = y (4) = 4,01 2 -4 2 = 16,0801-16 = 0 , 0801.

Az érték a származék az érintési pont és x0 az értéke a lejtőn a tangens (geometriai jelentése a-származék). Van: F „(x0) = tga = 1 → α = 45 °, mivel TG45 ° = 1.

A: A érintő a grafikonja ez a funkció határozza pozitív iránya az Ox tengely 45 ° -os szögben.

3. Derive általános képletű y = x n.

A differenciálás - cselekmény a megállapítás a származékot egy funkciót.

Amikor megtalálása általános képletű származékok használnak, amelyeket származik alapján a meghatározása a származék, ugyanúgy, mint azt abból a képlet-származék fok: (x n) „= nx n-1.

Táblázat származékok könnyebb lesz megjegyezni, kiejtésével megfogalmazásokat:

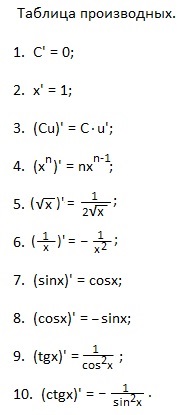
1. A-származék állandó nulla.

2. X-bar egyenlő egy.

3. A konstans tényező lehet venni kívül származék.

4. A származék mértékben index = a termék a mértékben mértékétől ugyanezen bázissal, de eggyel kevesebb, mint az index.

5. A származék a gyökér egyenlő egy osztva két egyforma gyökér.

6. A származék egységek, osztva a X értékéül mínusz egy, osztva X a téren.

7. A származék szinusz koszinusz.

8. A származék koszinusz negatív sine.

9. A származék a tangense egyenlő egy osztva a tér a koszinusz.

10. A származékot kotangensét egyenlő mínusz egy, osztva a tér a szinusz.

Tanulunk a szabályokat a differenciálás.

1. Származtatott algebrai összege egyenlő az algebrai összege származtatott kifejezései.

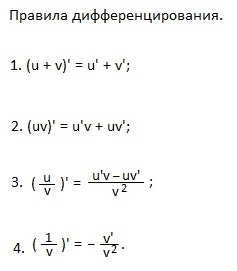
2. Az a derivatív termék megegyezik a termék a származék az első tényező, plusz a második termék az első tényező, hogy a második származékot.

3. A származék „y” osztva az „CE” a frakciót, amelyben a számláló „bar szorozva a” CE „mínusz” időnként a bárban ve „és a nevező -” ve a téren. "

Oldal 1 1 1