20180228 Miért van az elektronban fél-egész spin, és a fotonnak egésze van (n
Kollégám megkérdezte ezt a kérdést.
- Ezt a kérdést gyorsan megválaszolhatja, ha tudja, mi a spin. Tudja?
A fizika tankönyv lehet olvasni, hogy ez a kvantum tulajdonság az elemi részecskék, amely megfelel a klasszikus fizika, mechanikai tehetetlenségi nyomaték, azaz a A forgatás (szó szerint forgatva) a forgatás tehetetlenségét jellemzi. Egy bolygó (bolygókerekes modell Rutherford elektronok atom, mint bolygó körül forog egy atommag) egyenlő a termék a tehetetlenségi nyomatéka a tömege, hogy a sugár, azaz a távolság a naprendszer központjától.
Ha egy elektronot egy olyan gyűrű képvisel, amely betölti az első Bohr pályát, akkor a tehetetlenségi nyoma nem változik, mert Az elektron minden részének sugara ugyanaz marad. Igaz, ez nem lesz a sajátunk, hanem az elektronok orbitális pillanata, ami valójában az egész.
Mi a centrifugálás az elektrongyűrű-modell esetében? Miért van a fele az orbitális pillanat?
Képzeld el, hogy egy rakétán repül körkörös pályán. Ebben az esetben az orbitális szögsebessége egyenlő az egységgel (ha az orbit sugarát egységként vesszük). Mi lesz a spinod? Képzeld el, hogy a rakéta a tengelye körül forog. Ez az elforgatás megfelel az elektron spinnak. Nyilvánvaló, hogy a tehetetlenségi nyomaték a rakéta sugarától, nem a pályától függ.
Ha feltételezzük, hogy a sugár a rakéta a klasszikus sugara egy elektron, akkor meg kell forgatni a tengelye körül, így az űrhajósok préselt centrifugális erő a falnak a rakéta fog mozogni a középpontja körül meghaladó sebességgel a fénysebesség idők tíz!
Ha a fény nem tud gyorsabban mozogni, mint a fény, akkor a tehetetlenség forgási pillanata nem lehet rendes mechanikus pillanat. Ez az érvelés a hátulról indul, ami a klasszikus fizika keretében nem magyarázható.
Ha a „klasszikus” elektron sugárral, a feltételezéssel számítva, hogy az elektron van egy gömb alakú, úgy tervezték, helyesen, például azért, mert egy elektron más-más alakú, a sebesség a „felület” az elektron lecsökkenhet a fény sebessége, mint lényegében az elektron ( hurkolt elektromágneses sugár).
Tekintettel arra, hogy a gerenda alkotó „test” Egy elektron cirkulárisan polarizált (balkezes pozitron szemben), könnyű kitalálni, hogy része az energia tartalmazza a polarizáció mozgás, azaz a a "rakéta" középpontjának körüli forgatásban.
Ennek a forgásnak az iránya az "orbitális" területétől függ, vagyis az "orbitális" területétől. a hurkolt elektronsugár szegmense. Az elektron egy fele úgy fog megjelenni, mintha az óramutató járásával megegyező irányba forgatnánk, míg a második fél az ellenkező irányba forog. A közelben és távolabbi pontokban a forgás megfordul, ezért ezeken a pontokon úgy tűnik, hogy megállunk értünk. Ha ezt a látszólagos forgást integráljuk, ha a mínuszjelet a félben lévő pluszra változtatjuk (így nem kapunk nulla értéket), még mindig csak a fele van. És talán nem fogjuk meg.
Képzeld el, hogy gondozza a távozó rakétát, majd a rakéta kering a Föld, és úgy tűnik, hogy kezdett forgatni az ellenkező irányba, míg benn biztos lehet benne, hogy a forgatva balra spirál és forog, de ha visszatekintünk, akkor látni fogod, hogy az ég ellenkező irányban forgott.
Így kiderül, hogy az elektron fele egy irányba forog, a másik pedig - a másikban. Ezért a "különösség", amely abból áll, hogy az elektron spin irányul az orbitális mozgás mentén vagy ellene.
De ha az elektronnak csak az a fele fordul el egyik irányban, akkor nyilvánvaló, hogy az egész, pl. hát, nem lehet.
Ami a fotont illeti, akkor minden oldalról nézzük, láthatjuk, hogy teljesen egy irányban fordul. Azonban be kell zárnunk, és a fele az ellenkező irányba fordul. És bármit is mondhat, fél fordul az óramutató járásával megegyező, és félig ellen.
Így válik lehetővé a klasszikus ötletek visszatérése a mikrovilág méretarányára. A mikro-világ klasszikus modelljeiről a Nanomir enciklopédia legelső szövegei találhatók.
Általában nem kedvelem a magyarázatot, miért van az elektronban fél-egész centrifugálás. A Rutherford-atom modelljében az elektronot bolygógömbként ábrázolták, amely a tengelye körül forog. Nyilvánvaló, hogy a forgástengely forradalmasításához valójában a bolygót arra kell kényszeríteni, hogy megváltoztassa a forgásirányát. Ez bizonyos energiát igényel. Ha megfordítjuk a gyűrűs elektront, az orbitális irány megváltozik az ellenkező irányba, és a "rakéta forgatása" a tengelye körül nem változik, mert ha ez egy bal szárnyú mozgalom, akkor ez marad. Kiderül, hogy kevesebb energiát kell fordítanunk a "gyűrű" elektronika átirányítására, mint a "bolygók" -elektronok. És még kétszer kevesebb ez az energia, vagy nem két - külön kérdés. Az a tény, hogy egy atom elektronhéjában az elektron nehéz megfordulni, mivel kiderül, hogy a szomszédos elektronok számára azonos nevű orientált pólus. Nyilvánvaló, hogy amint felszabadítjuk, ismét stabil mágneses helyzetbe tér vissza. Ha azonban fogjuk bővíteni távol az atom, akkor szinte nem energiát fogyaszt, különösen azért, mert fékezéskor megtesszük az energia, amely költik a gyorsulás (szögletes).
Itt találjuk, hogy az elektron spin társul az "orbitális" mozgásának új irányba, mivel ha viszont a gyűrű mágnes, amit modellezni az elektron ténylegesen változik az irányt a hullám előtt a másik, míg a továbbra is azonos polarizációs iránya a mozgás (forgatás „rakéta” a saját tengelye). Ha a polarizációs mozgás "súlya" a teljes elektron mozgásának felét, akkor az elektrongyűrű elforgatásával ténylegesen megváltoztatjuk az intra-strukturális mozgás második komponensét, azaz csak "orbitális". Ennek során az elektron belső szerkezetének csak a felét változtatjuk. By the way, ha az elektronon belüli "polarizáció" és "orbitális" mozgások a szabadság két fokát képviselik, akkor az egymás közötti energiát egyenlően kell elosztani. Ez a tulajdonság sok szabadságú rendszer esetén érvényes.
Lehetséges, hogy a kvarkokban a szubstruktúrák 1/2 és 1/6-os tömegűek az elektron töltéssel, mert az egyik alszerkezetnek háromszor nagyobb a szabadsága, mint a másik. Például, az embernek csak a szabadság tangenciális mértéke van, míg a másiknak mindhárom szabadság térbeli fokozata vagy egy tangenciális és - mondjuk - két vibrációs szabadsági fokja van. El tudod képzelni, hogyan viselkedik a gyűrűben lezárt tavasz? De a vibrációs szabadságfokok már egy másodikrendű folyamat. Valószínű, hogy az elsőrendű eljárásnak pontosan három térbeli szabadsága van.
Ezt jobban magyarázza az ábrán.
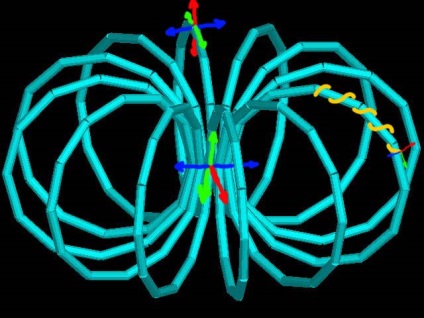
A sárga vonal olyan alépítményt mutat, amelynek "tömege" 1/2. Ő rendelkezik a mozgás szabadságának mindhárom fokával.
A világoskék szerkezet egy olyan szerkezetet mutat, amelynek "tömege" 1/6. Csak "zöld" szabadsága volt. A "kék" és a "piros" a szomszédos kvark hurkok közötti mágneses kölcsönhatás által "kapcsolódnak".