Rgz Matan 12 Var
Dana T - periodikus függvény f (t)
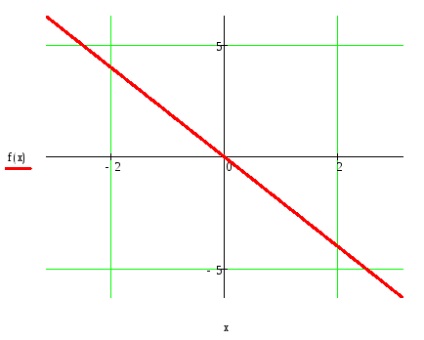
Indokolja a lehetőségét bomlása f (t) egy Fourier-sor, hogy létrehozzák a formáját a konvergencia a Fourier-sor f (t).
Dirichlet Tétel: Ha a T - periodikus függvény f (t) megfelel a Dirichlet feltételeket, amelyek vagy egy zárt intervallum hossza T:
Folyamatos vagy véges számú pontot diszkontinuitás az első fajta
A monoton, vagy véges számú maximumok és minimumok
A Fourier-sor konvergál az egész T tengely és az összeg a Fourier-sor megegyezik az f (t) minden pontján e függvény folytonos a ponton t0 diszkontinuitás az első fajta funkciók f (t) az összegével egyenlő a Fourier sor az f függvény (t) megfelel a konvergencia feltételeket az átlagos.
Ljapunov Jelenség: Ha a T - periodikus függvény f (t) kielégíti a feltételeket a szakaszonként folyamatos és négyzetesen integrálható, akkor a Fourier-mean-square konvergálnak f (t).
Döntetlen a grafikon az összeg a Fourier-sor.
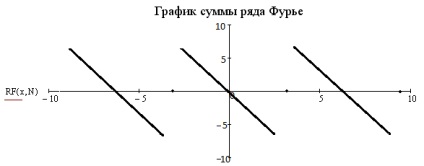
Jelen előre trigonometrikus függvény Fourier korábban:
b) kiszámítja az együtthatók a Fourier sor.
Az együtthatók a Fourier-sor
Trigonometrikus bomlás definiált függvény egy Fourier-sor
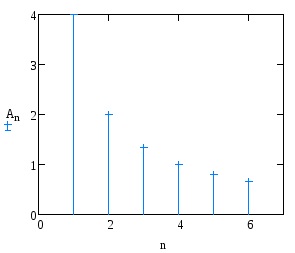
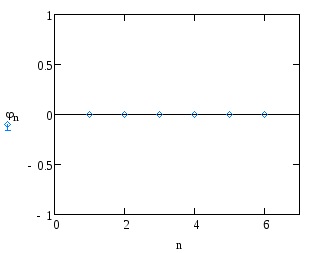
Építsünk amplitúdó és fázis spektrumok a függvény.
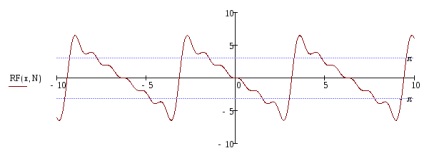
Határozza meg a számát harmonikusok expansion funkciót egy Fourier-sor tartalmazó összege nem kevesebb, mint 90% az energia.
Annak meghatározására, számának harmonikusok tartalmazó in toto legalább 90% az energia eredetileg kiszámítani az energia által bevezetett egyes harmonikus külön-külön a következő képlet:
A hozzájárulást a harmonikus a teljesítmény
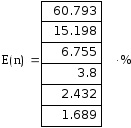
Számítsuk ki a közötti négyzetes átlagos hiba az eredeti f (t) és a részleges Fourier összeget t tartozó span feladat.
A képlet az átlagos négyzetes hiba:
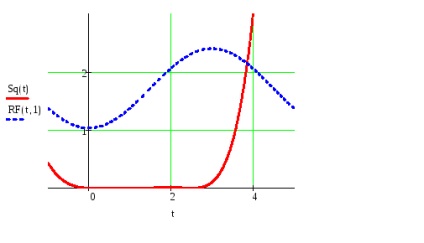
Készítsük el a grafikus meghatározott funkciók és részösszegként a Fourier sor t tartozó értékek intervalluma megbízás f (t), figyelembe véve a több harmonikus egy bizonyos bekezdés №5.
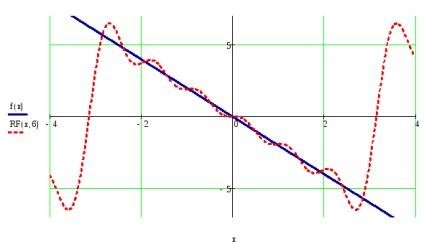
Ábrázoljuk a négyzetes eltérés funkciót és részleges összege intervallum t hozzárendelés f (t).
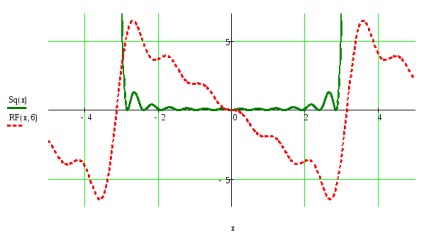
A függvény egy véges intervallumban, építésére periodikus kiterjesztését egy előre meghatározott módon.
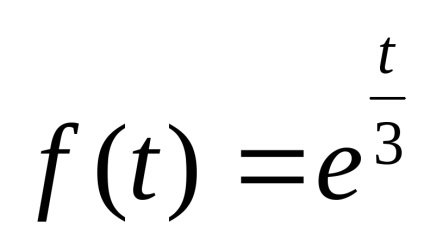
Indokolja a lehetőségét bomlása f (t) egy Fourier-sor, hogy létrehozzák a formáját a konvergencia a Fourier-sor f (t).
A f (t) kielégíti a Tétel Dirichlet:
Dirichlet Tétel: Ha a T - periodikus függvény f (t) megfelel a Dirichlet feltételeket, amelyek vagy egy zárt intervallum hossza T:
Folyamatos vagy véges számú pontot diszkontinuitás az első fajta
A monoton, vagy véges számú maximumok és minimumok
A Fourier-sor konvergál az egész T tengely és az összeg a Fourier-sor megegyezik az f (t) minden pontján e függvény folytonos a ponton t0 diszkontinuitás az első fajta funkciók f (t) az összegével egyenlő a Fourier sor az f függvény (t) megfelel a konvergencia feltételeket az átlagos.
Weierstrass tétel: Ha a T - periodikus függvény f (x) bármely intervallumban zárva. Például a [-T / 2, T / 2] kielégíti a folytonosság és az f (-T / 2) = f (T / 2), akkor a Fourier-sor trigonometrikus konvergál az f (x) egyenletesen.
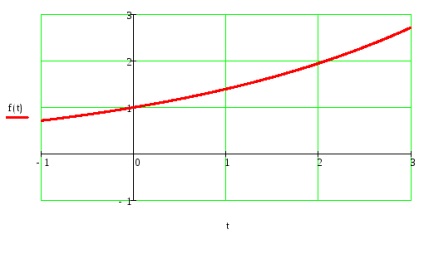
Döntetlen a grafikon az összeg a Fourier-sor.
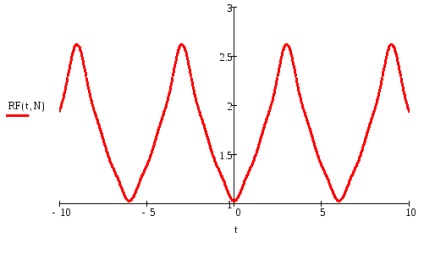
Jelen előre trigonometrikus függvény Fourier korábban:
b) kiszámítja az együtthatók a Fourier sor
Az együtthatók a Fourier-sor
Trigonometrikus bomlás definiált függvény egy Fourier-sor
Építsünk amplitúdó és fázis spektrumok a függvény.
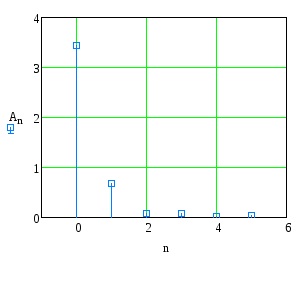
Határozza meg a számát harmonikusok expansion funkciót egy Fourier-sor tartalmazó összege nem kevesebb, mint 90% az energia.
A hozzájárulást a harmonikus a teljesítmény
Számítsuk ki a közötti négyzetes átlagos hiba az eredeti f (t) és a részleges Fourier összeget t tartozó span feladat.
Készítsük el a grafikus meghatározott funkciók és részösszegként a Fourier sor t tartozó értékek intervalluma megbízás f (t), figyelembe véve a több harmonikus egy bizonyos bekezdés №5.
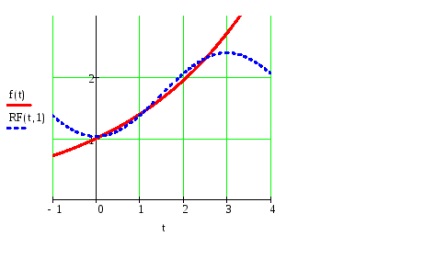
Ábrázoljuk a négyzetes eltérés funkciót és részleges összege intervallum t hozzárendelés f (t).