megmaradási
A kezdeti pillanatában mozgása a henger sebessége nulla, és a teljes mechanikai energia egyenlő lehetőségeket. Az átmenet egy vízszintes síkban a teljes mechanikai energia a henger összegével egyenlő a mozgási energia és helyzeti energia a henger. A törvény szerint a természetvédelmi teljes mechanikai energiát kapunk:
A potenciális energia a henger helyzete határozza meg a tömegközéppontja a henger vízszintes sík felett. Ezért :. ahol g - a nehézségi gyorsulás.
Mint ismeretes, henger gördülő egy sík felületre lehet tekinteni, mint egy rotációs szögsebességgel # 969; körülbelül egy pillanatnyi forgástengely átmenő közötti érintkezési vonal a hengeres felület és egy síkban. Ábra pillanatnyi forgástengely áthalad M pont merőleges a rajz síkjára. Következésképpen, a kinetikus energia határozza meg az expressziós
ahol I - tehetetlenségi nyomatéka a henger képest pillanatnyi forgástengely. Az ismert kifejezés a tehetetlenségi nyomatéka a henger tengelyéhez képest a szimmetria és Steiner tétele kapjuk:
Expression (1) tekintettel a (2) képletben és a (3) formájában
Egyenlet (4), hogy a szögsebesség # 969; alábbiak szerint:
A perdület L a henger való átmenetnél a vízszintes sík mentén irányul pillanatnyi forgástengely ábrán látható. modul lendület
válaszolni: # 969; = 72 rad / s; L = 2,7 (kg × m²) / s.
12. Két golyó, egy m1 tömege = 2,0 kg, a második m2 = 3,0 kg, a vízszintes síkban mozog, egymásra merőleges irányban felé és ütköznek teljesen rugalmatlanul. Keresse meg a labdákat az ütközés után sebességet. irányát és sebességét részét mechanikus energia labdákat, hogy átkelt a belső energia labdákat. Mielőtt az első labdát ütközési sebesség = 5,0 m / másodperc = 3,0 m / s.
döntés
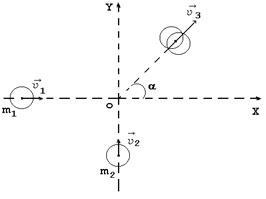
A vízszintes síkban XOY bevezetésére koordinátarendszerben. ábrán látható. 1. Az ütközés a golyók fordul elején a koordináta-rendszer. Teljesen rugalmatlan ütközés, ezért a golyó „összeragadnak”, és együtt mozog a sebesség. ábrán látható. 1. Egy külső erő (gravitáció) ható golyók, merőleges a vízszintes síkban és ezáltal a törvény lendületmegmaradás
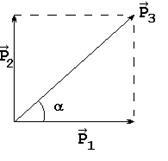
ahol - az első impulzus a labdát, mielőtt az ütközés; - Egy másik golyó lendülete az ütközés előtt; - impulzus golyók ütközés után. A természet a mozgás golyók és a törvény lendületmegmaradás, ebből következik, hogy a irányvektorok meg kell felelnie ábra. 2, és ha a modulok kapcsolatos vektorok vagy
Egyenlet (2), így a sebesség:
szög # 945;, amely jellemzi az irányt a sebesség. Megtalálható ábrából. 2. az alábbi képlet szerint:
Amikor teljesen rugalmatlan ütközés mechanikai energiát csökkentett összeg testek # 916; W. került át a belső energia labdákat. Mozgás egy vízszintes síkban, így a mechanikai energia a rendszer miatt a mozgási energia a golyók. Végül, értékei # 916; W kellene
A: = 2,7 m / s; # 945; = 42º; # 916; w = 20 J.
13. Zhukovskogo pad forog n1 = 1,0 v / a személy, aki a vízszintesen elhelyezett közepén a fém rúd tömege, m = 5,0 kg, és hossza L = 1,5 m. Adjuk Emberi fordulatszám n2 és tökéletes munkát A ., ha ő fog fordulni a rúd függőleges helyzetben. A tehetetlenségi nyomaték és a humán padon I0 = 5,0 kg # 8729; m².
Megoldás Forgatás személy a rúd bekövetkezik egy függőleges tengely körül, a pillanatnyi külső erők, amelyhez képest nulla. Ezért L a perdület a függőleges tengely körül forgó változatlan marad, ha a rúd, azaz a. F .. vagy (1)
ahol I1 és # 969; 1 - a tehetetlenségi nyomaték és a szögsebesség humán rúd vízszintesen elhelyezett; I2 és # 969; 2 - a tehetetlenségi nyomaték és a szögsebesség emberi rudat függőlegesen helyezkedik. szögsebesség # 969; és a fordulatszám időegység kapcsolja össze
A tehetetlenségi nyomaték Ic rúd merőleges tengely körül, hogy a rúd és a középpontján átmenő a tömegek. ezért
Elforgatásával a rúd függőleges helyzetbe a tehetetlenségi nyomaték nulla lesz. Következésképpen, (4) behelyettesítve egyenlet (2) - (4) a általános képletű (1), kapjuk :. Ez feltételezi, hogy az értéke n2:
A. A munka a tökéletes ember fordulóján a rúd egyenlő a változás kinetikus energia. ezért
Problémák független megoldás
1.44. Platform, mint tárcsa forog a tehetetlenség a függőleges tengely körül a frekvenciájú n1 = 14 perc -1. A szélén a platform egy ember. Amikor az emberek mozgatni, hogy a központ a platform, a frekvencia nőtt n2 = 25 perc -1. Emberi tömeg M = 70 kg. Határozza meg a súlya a platform. A tehetetlenségi nyomaték a személy számít egy anyagi pont.
1.45. Man m0 = tömege 60 kg alatt van a rögzített platformon súlyú m = 100 kg. Milyen gyakorisággal n fog forogni a platform, ha egy személy mozog egy r sugarú kör = 5,0 m körül a forgástengely? Speed emberi relatív mozgást a platform u0 = 4,0 km / h. R = sugara a platform 10m Read platform homogén lemez, és az emberi -. Point tömeg.
1.46. A labda legurul a ferde sík magassága h = 90 cm. Mi lesz a lineáris sebesség abban a pillanatban a labdát, ha legurul a ferde sík? labda tehetetlenségi nyomaték J = 0,40 m × R 2.
1.47. Két golyó mozog egymás felé az X tengely mentén A súly a első labdát m1 = 0,20 kg, a tömeg a második labdát m2 = 0,30 kg. Az ütközés előtt sebessége vetítési golyó tengely = 1,0 m / s = -1,0 m / s. Keresse meg a vetítés a sebesség golyó, és miután a központi abszolút rugalmas ütközés.
(= -1,4 m / c; = 0,60 m / c)
1.48. Egy vékony, homogén rúd L hosszúságú lehet forgatni egy vízszintes tengely körül áthaladó a végén a rúd merőleges. A rudat elutasította 90 ° az egyensúlyi helyzetből, és megjelent. Határozza meg a sebessége u az alsó rúd vége idején áthaladását egyensúlyt.
1.49. Egy vékony, homogén rúd hossza L, M a tömeg szabadon forog egy vízszintes tengely körül áthaladó egyik végéhez. A rúd vízszintesen és megjelent. Elhanyagolása súrlódás, meghatározza a szögsebesség a rúd idején áthaladás az egyensúlyi helyzet. Ábrázoljuk a szöggyorsulás a rúd közötti szög a rúd és a horizont.
1.50. A szilárd homogén labda legurul a ferde sík 5,0 m hosszúságú. A szög a síkja a horizonton a = 30 °. Határozzuk meg a sebessége a labdát a végén a ferde sík, míg a labda mozgása a vízszintes felületre, és minőségileg a telek kinetikus energiája a labdát, mint az idő függvényében. Energiaveszteség elhanyagolható. A tehetetlenségi nyomaték egy olyan tengely körül közepén áthaladó tömeg, J0 = mR 2.
(U = 5,9 m / s; t = 1,7 c)
1.51. Tömör henger tekercs egy vízszintes felületre t idő = 3,0 c és megáll utazás után a távolság 9,0 m. Annak meghatározására, a súrlódási együttható, feltételezve, hogy állandó. A kvalitatív függését a kinetikus energia a test mozgásának függvényében.
1.52. Val tömege m = 50 kg, és a sugara R = 5,0 cm forgott n = 10 ford / s. A hengeres felület a fékpofa erővel nyomjuk F = 30 N, és miután 8,0 másodperc után a fékezés kezdete a tengely megállt. Annak megállapításához, a súrlódási együttható, feltételezve, hogy állandó. Ábrázoljuk a szögsebesség és szöggyorsulásakor a tengelyen, az idő függvényében a fékezési intervallumban.
1.53. A labda és a lemez ugyanolyan szilárd tömeg és gördülési nélkül csúszik a vízszintes felületre azonos állandó sebességgel. A mozgási energia a labda W1 = 70 J. Határozzuk meg a kinetikus energia a W2 lemezen. Find az arány a perdület szerveire LZ1 / LZ2 a pillanatnyi forgástengely ha R1 / R2 = 0,7.
1.54. Testtömeg M felfüggesztheti a szál hossza L. A lövedéktest m tömegű esik, és ez ragadt a menet után, hogy eltér egy szög. Keresse meg a sebességet a golyó. Tegyük fel, hogy a teljes testtömeg M koncentrálódik L távolságra a felfüggesztés pontjától.
1.55. Mennyi időt gördül henger ferde sík hossza l = 2,0 m, magassága h = 0,10 m, feltételezve, hogy nem csúszik? Minőségi építeni függőség a kinetikus és potenciális Wk Wp teljesítményű henger az idő függvényében.
1.56. Két golyó tömegek m1 = 10 kg és 15 kg, m2 = a húrok lógott hossza L = 2,0 m, hogy a golyók érintkeznek egymással. A kisebb labda lett hajlítva szögben J = 60 °, és megjelent. Határozzuk meg a magasságot, hogy a nő mindkét golyó az ütközés után. Hit golyókat venni rugalmatlan.
1.57. A henger tömege m1 = 3,0 kg, és a sugara R = 10 cm, pihen egy síkban hiányzik golyó tömege m2 = 9,0 g, repülő sebességgel U0 = 60 m / s. A golyó repül síkjával párhuzamos magasságban h = 0,12 m-re, és merőleges az alkotója a henger. Tekintettel csapás teljesen rugalmatlan, megtalálják a lineáris sebessége a henger tengelyével, a szögsebesség a henger. Slip henger elhanyagolt.
1.58. Body a tömegek m1 és m2 vannak csatlakoztatva súlytalan és nyújthatatlan fonál, amely átjut a tömegegységre m. szerelt az asztal szélére. m1 a test felületén a táblázat a biztosított állapotban. M2 test lóg szabadon. A t = 0 a test m1 megjelent, és a rendszert mozgásba. Feltételezve, hogy a súrlódási tényező az asztal és a test m1 egyenlő m, elhanyagolva a tologatós, és a menet a súrlódás a tengelye a blokk, meg a munka a súrlódási erők az első t másodperccel a rajt után a mozgás. Blokk tekinthető egységes lemezt.
1.59. Egy acélgolyót tömegű m = 8 g repülő vízszintes sebességgel 600 m / s, belép a bár tömeg M = 4m. csatlakozik a falhoz egy rugó merevsége k = 24 kN / m. Feltételezve, hogy a pályán a labdát, és a felületre merőlegesen a rúd tengelye egybeesik a tavaszi, hogy nagyságának meghatározásához maximális tömörítés a tavasszal, amikor a stressz volt:
1) teljesen rugalmatlan; 2) teljesen rugalmas.
Jegyezzük fel a variáció a deformáció a tavasz az idő függvényében az 1. és 2. esetben.
1.60. A dugattyú szerelt rugó merevsége k = 10 kN / m, miután a lekvárt az abban vízszintesen repül sebességgel u = 520 m / s Bullet 20 g eltoljuk x = 8 cm. Határozza meg a súlya a dugattyú M. erő, ha a súrlódást a henger fala 900 N.
1.61. A szálat a terhelés felfüggesztett rajta elutasította az a szög, és megjelent. Mekkora szögben b tér el a szálat a terhelést, ha a mozgás késni fog egy csap fel a függőleges közepén a menet? Építeni a minőségi kapcsolat az áruk az idő sebességét, feltételezve, hogy az energiaveszteség a rendszerben bekövetkezik.
1.62. Hoki korong, amelynek a kezdeti sebessége u = 5,0 m / s; áthalad, mielőtt a hatása a fedélzeten pad path S = 10 m. A súrlódási tényező jégen alátétek 0,10. Figyelembe véve a hatását a fórumon teljesen rugalmas és elhanyagolja a légellenállás, melyik utat fogja át a korong az ütközés után. Ábrázolva ux = f (x), feltételezve, hogy a pozitív iránya az X tengely a fedélzeten.
1.63. Ember áll az álló kocsi és a vízszintes dobás kő tömege m1 = 2,0 kg sebességgel u = 8,0 m / s. Határozza meg, hogy milyen munkát egy ember teszi, ha dobott, ha a tömeg a kocsi a férfi m2 = 140 kg. Ábrázoljuk a függőség a munka A = f (m2), ha m2 - változó.
1.64. Tornász „csavarják a nap” a mezőnybe. Feltételezve, hogy a teljes tömeget m tornász koncentrálódik a tömegközéppontja és a sebesség tornász a tetején nullával egyenlő, hogy meghatározzuk a ható erő a kezében tornász a legalacsonyabb ponton. Ábrázoljuk a függőleges sebesség komponenssel idő függvényében tornász uy = f (t). Mivel a kiindulási pont, hogy a felső pozícióban a tornász. Friction elhanyagolt.