Egyetemes tömegvonzás, fizika
1. Az egyetemes tömegvonzás törvénye
Azt már tudjuk, hogy az összes a testek vonzó erők, az úgynevezett nehézségi erőre.
Hatásuk nyilvánul például hogy a testek esik a földre, a Hold körül forog a Föld és a bolygók keringenek a nap körül. Ha a gravitáció eltűnt a Föld volna eltérni a Nap (ábra. 14.1).
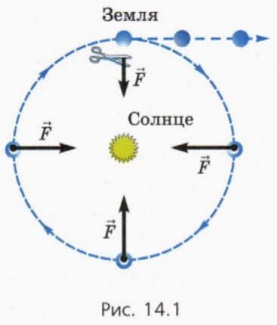
Ő fogalmazta egyetemes tömegvonzás törvénye a második felében a 17. században, Isaac Newton.
Két anyagi pont tömege m1 és m2 jelentése R távköznyire, rajzolt erők egyenesen arányos a termék tömegére és fordítottan arányos a távolság négyzetével közöttük. Minden tápegység
Az arányossági tényező G a gravitációs állandó. (A latin „Gravitas.” - súlyossága) mérések azt mutatták, hogy
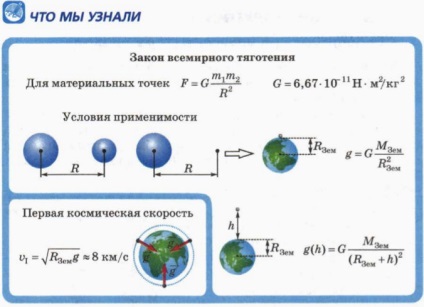
G = 6,67 * 10 -11 Nm 2 / kg 2 (2)
A gravitáció törvénye feltárja másik fontos tulajdonsága testsúly: ez az intézkedés nem csak a test a tehetetlenség, hanem a gravitációs tulajdonságait.
1. Mik a vonzóerők a két részecske egyenként 1 kg, található egy 1 m távolságra egymástól? Hányszor van ez az erő nagyobb, vagy kisebb, mint a tömeg egy szúnyog, melynek tömege 2,5 mg?
Egy ilyen kis értéke a gravitációs állandó megmagyarázza, hogy miért nem vesszük észre a gravitációs vonzás között a tárgyak körül bennünket.
2. Becsüld erejét gravitációs vonzás két ember között, a parttól 10 m-re egymástól.
gravitáció láthatóan megmutatkoznak csak ha legalább az egyik kölcsönható testek egy hatalmas tömeg - mint például egy csillag vagy egy bolygó.
3. Hogyan lesz a vonzóerő két lényeges ponton, ha a köztük lévő távolság növelése 3-szor?
4. Két anyagi pont m tömegű mindegyik vonzott olyan erővel F. Mivel erő vonzza az anyagi pont 2m tömegű és Zm, amelyek az azonos távolságra?
2. Mozgalom a bolygók a Nap körül
A távolság a nap bármely bolygó sokszor a méret a Nap és a bolygók. Ezért, amikor a mozgások a bolygók tekinthető lényeges pontokon. Következésképpen a vonzóerő a bolygó a Nap
ahol m - a bolygó tömegének, MS - tömege a Nap, R - távolság a Nap a bolygó.
Azt feltételezzük, hogy a bolygó mozog a Nap körül egyenletesen kerületén. Ekkor a sebesség a bolygó található, tekintettel arra, hogy a bolygó gyorsulás a = v 2 / R a vonzóerő F a Nap és az a tény, hogy megfelelően Newton második törvénye alapján F = ma.
5. Igazoljuk, hogy a sebesség a bolygó
Ebből a képletből következik, hogy minél nagyobb a sugara a pályára, a kisebb a sebessége a bolygó.
6. A sugara a Szaturnusz pályáján közel 9-szer nagyobb, mint a sugara a Föld pályáját. Keresse orálisan, ami nagyjából megegyezik a sebesség Saturn, amikor a Föld mozog a pályáján sebességgel 30 km / s?
Idővel egyenlő egy keringési idejének T, bolygó, mozgó v sebességgel, áthalad utat egyenlő a kerületének hossza R sugarú
7. Bizonyítsuk be, hogy a keringési idejének a bolygó
Ebből a képletből következik, hogy minél nagyobb a sugara a pályára, a nagyobb időszak bolygó forgása.
8. Kérjük, értékelje az keringési ideje a Szaturnusz (a földi év).
9. Bizonyítsuk be, hogy az összes bolygó a Naprendszer
Tip. A (5) képlet.
Tól (6) következik, hogy az az összes bolygó egy kocka sugarának aránya a Naprendszer a tér ugyanazon kezelési időszak. Ez a minta (az úgynevezett Kepler harmadik törvénye) talált német tudós Johannes Kepler eredményei alapján a hosszú távú megfigyelések a dán csillagász, Tycho Brahe.
3. A feltételek alkalmazhatóságát a gravitáció törvénye
Newton bebizonyította, hogy a képlet
A vonzóerő két lényeges ponton is használható:
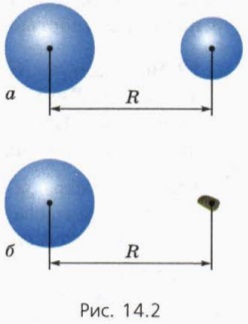
- homogén gömbök és gömbök (R - távolság a középpontok között a golyó vagy golyók, ábra 14.2 a.);
- a homogén golyó (gömb), és egy anyagi pont (R - távolságra a központtól a labda (gömb), hogy a tömeges pont, ábra 14.2, b.).
4. A gravitációs erő és a törvény az egyetemes tömegvonzás
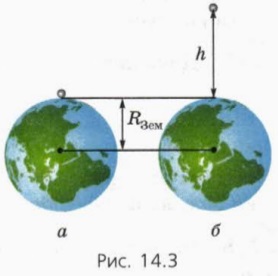
A második feltétel fentiek azt jelentik, hogy a képlet szerinti (1) meg lehet találni vonzereje bármilyen formában, hogy homogén labda test, ami sokkal nagyobb, mint a test. Ezért, az alábbi képlet szerint (1) meg lehet számítani a gravitációs erő a test földeket található a felületén (ábra. 14.3, a). Kapunk egy kifejezés a gravitációs erő:
(Földgömb nem homogén, de lehet tekinteni egy gömbszimmetrikus. Ez elegendő ahhoz, hogy lehetővé tegye a felhasználást általános képletű (1).)
10. Mutassuk meg, hogy közel a Föld felszínét
ahol MZem - a tömege a Föld RZem - sugara.
Tip. Használata képletű (7), és hogy az Fm = mg.
A képlet (1), találunk a nehézségi gyorsulás h magasságban fölött a Föld felszínén (ábra. 14.3, B).
11. Bizonyítsuk be, hogy
12. Mi a gyorsulás szabadesés fölötti magasságban a Föld felszínén, egyenlő a sugár?
13. Hányszor a nehézségi gyorsulás a Hold felszínén kisebb, mint a Föld felszínén?
Tip. A (8) képletű, ahol a tömeg és sugara a föld helyett a tömeg és sugara a hold.
14. A sugara a csillag fehér törpe egyenlő lehet a sugara a Föld, és annak tömegét -, mint a Nap Mi a súly kg súly a felszínen, mint a „törpe”?
5. Az első kozmikus sebesség
Képzeljük el, hogy egy nagyon magas hegyre létre egy hatalmas fegyvert, és lőni belőle a vízszintes irányban (ábra. 14.4).
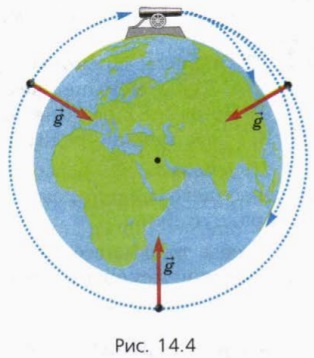
Minél nagyobb a kezdeti lövedék sebessége, annál távolabb fog esni. Nem esik egyáltalán, ha felveszi a kezdeti sebességét úgy, hogy mozgott a Föld körül egy kört. Repülő körpályán, a lövedék azután válik mesterséges műhold a Föld.
Hagyja, hogy a shell-satellite mozog egy alacsony Föld körüli pályán (ún pályára, amelynek sugara lehet egyenlővé tenni a Föld sugara RZem).
Egyenletes kerületi mozgást a műholdas mozog a centripetális gyorsulás a = V2 / RZem ahol v - sebessége a műhold. Ez a gyorsulás a gravitáció hatására. Ezért, a műholdas mozog a gravitációs gyorsulás, középpontja felé irányuló, a föld (ábra. 14.4). Ezért, a = g.
15. Mutassuk meg, hogy menet közben egy alacsony Föld körüli pályán műhold sebessége
Tip. Használata képlet a = V 2 / R a centripetális gyorsulás és az a tény, hogy a közlekedés során egy olyan pályán sugara RZem műholdas gyorsulás egyenlő a gravitációs gyorsulás.
sebesség v1. amely szükséges, hogy tájékoztassa a testet úgy, hogy mozog a gravitáció mentén körpályán közel a Föld felszínét, az úgynevezett első helyet sebességét. Ez nagyjából megegyezik a 8 km / s.
16. Express az első helyet sebességgel a gravitációs állandó, a tömeg és Föld sugara.
17. Értékelje hányszor a szökési sebesség a Hold kisebb, mint a Föld. Tegyük fel, hogy a tömeg a Hold 81-szer kisebb, mint az a tömeg, a Föld és a Hold sugár kisebb, mint 3,7-szerese a Föld sugara.
Tip. A képletben az előzőekben kapott munkát, módosíthatja a tömeg és sugara a föld a súly és a sugara a hold.
A test örökre elhagyta a közelben a Föld, köteles azt a sebességet körülbelül 11,2 km / s. Ezt nevezik a szökési sebesség.
6. mért gravitációs állandó
Ha tekinthető ismert gyorsulás g alá közel a Föld felszínén, a Föld tömege és sugara, az értéke a gravitációs állandó G könnyen meghatározható a következő képlettel (7). A probléma azonban az, hogy amíg a végén a 18. század, nem volt mérhető a tömege a Földet.
Ezért, hogy megtalálja az érték a G gravitációs állandó, szükséges volt mérni a vonzóerő két testület között, ismert tömegű, található egy bizonyos távolságra egymástól. Végén a 18. század, ez a tapasztalat sodorhatják az angol tudós, Henry Cavendish.
Ő lógott egy vékony elasztikus szál fény vízszintes rúd kis fém golyókat a és b, valamint a forgásszög a menet mért vonzó ható erő a golyók a nagy fém golyókat az A és B (ábra. 14,5). Kis elfordulási szögek a menet tudósok mérik az elmozdulás a „nyuszi” egy tükör csatlakozik a menet.
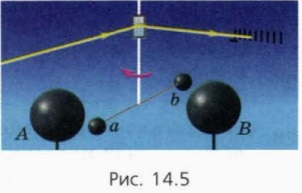
Ez a tapasztalat Cavendish képletesen az úgynevezett „súlya a Föld”, mert ez az élmény az első alkalommal mérni lehet a föld tömege.
18. Express a súlya a föld-G, G és RZem.
További kérdések és feladatok
19. Két hajó súlya 6000 tonna minden rajzolt erőssége 2 Nm. Mi a távolság a hajó?
20. A mi kényszeríti a Nap hívja a földet?
21. Milyen erő férfi 60 kg testtömegű vonzza a nap?
22. Mi a nehézségi gyorsulás egy bizonyos távolságra a földfelszín, átmérője megegyezik?
23. Hányszor gyorsulás a Hold miatt a vonzereje a föld, kevesebb, mint a gyorsulás szabadon eső egy a Föld felszínén?
24. Nehézségi gyorsulás a Mars felszínén 2.65-szor kisebb, mint a gyorsulás szabadesés a Föld felszíne. Mars megközelítőleg egyenlő a sugárral 3400 km. Hányszor tömege Mars kisebb, mint a Föld tömege?
25. Mi az az időszak, a Föld forgása mesterséges műhold alacsony Föld körüli pályán?
26. Mi a szökési sebesség a Mars? Mars Súly 6,4 x 10 23 kg-os, és a sugara 3400 km.