Bemutató 1 cikloist görbe, amely leírja egy pontot rögzített egy kört,

Előadás. „1 cikloist görbe, amely leírja egy pontot rögzített körön gördülő egyenes mentén az úgynevezett cikloist cikloist elhalasztja a képre.” - átirata:

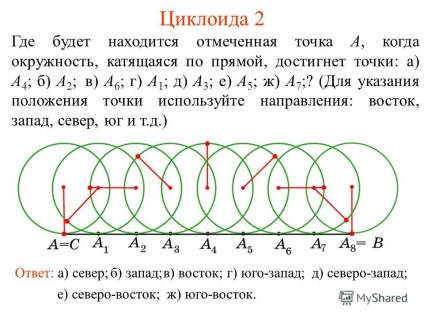
1 1 ciklois görbét, amely leírja egy pont rögzítve egy kör mentén gördülő egy egyenes vonal nevezzük ciklois. Elhalasztása kép cikloist a AB szakaszt egyenlő a kerülete, azaz AB = 2πR. Azt ossza ezt a szegmenst 8 egyenlő részre által az A 1 A = B 8. Tudja meg, hol található a bázis pont, amikor egy kör mentén gördülő egyenes, eléri a B pont?

2 2 ahol cikloist kell jelölni a pont, amikor a kör mentén gördülő egy vonal eléri pont: a) A 4; b) A 2; a) 6; g) A 1; d) A 3; e) A 5; g) A 7. ;? (Ahhoz, hogy adja meg a helyzetét a felhasználás helyén irányban: kelet, nyugat, észak, dél, stb) Válasz: a) Észak-b) nyugatra c) keletre; d) irányban, és e) az észak-nyugati, e) északkeleti; g) délkeleti.

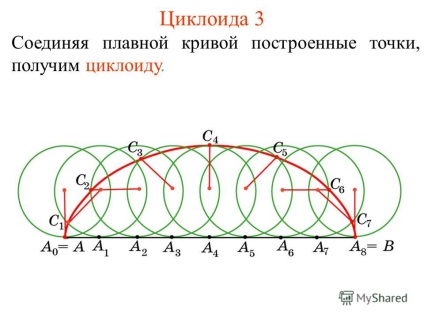
3 cikloist 3 áthidalása sima görbe a pontokat szerezni cikloist.

4 Ciklois mozgásban az első, aki elkezdte tanulmányozni a cikloist volt Galileo Galilei (1564-1642). Ő találta ki a nevet.

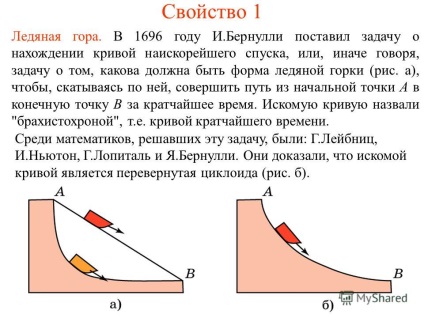
5. Az ingatlan 1 Ice Mountain. 1696-ban J. Bernoulli jelentette a problémát, a megállapítás a legmeredekebb ereszkedés görbe, vagy más szóval, a probléma, hogy mi legyen a jég formájában diák (ábra. A), úgy, hogy csúszik rajta, hogy utat a kiindulási pont, hogy a végpont a lehető legrövidebb idő alatt. Kötelező görbe úgynevezett „brachisztochron”, azaz Legrövidebb idő görbe. Között a matematikusok, hogy megoldja ezt a problémát a következők voltak: G. Leibniz, Newton, és G.Lopital Ya.Bernulli. Bebizonyították, hogy a szükséges görbe fordított cikloist (ábra. B).

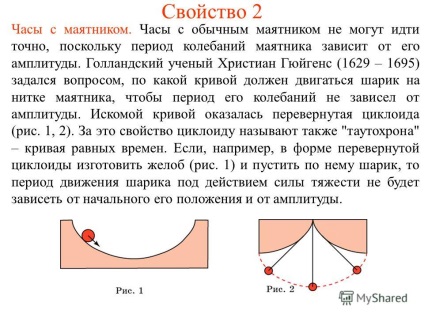
6. Az ingatlan 2 ingaóra. Nézd a hagyományos inga nem megy pontosan időszak inga oszcilláció függ a nagysága. Holland tudós, Christiaan Huygens (1629 - 1695) azon, hogy milyen görbe kell mozgatni a labdát egy string az inga az időszak oszcilláció független az amplitúdó. Kívánt ciklois görbét fordított (ábra. 1, 2). Mert az ingatlan cikloist is nevezik „tautohrona” - görbe egyenlő alkalommal. Ha például, formájában fordított ciklois legyártja csúszda (ábra. 1), és tegye le a labdát, az időszak a mozgás a labda a nehézségi erő hatására nem függ a kezdeti pozíció és annak amplitúdója.

7 1. tevékenység sugarú kör 1 tekercs a vonal mentén. Bizonyos távolságra a sorban lesz a C pont 1, ..., C 7. válasz. 1. 2. 1..

8 2. gyakorlat van cikloid hogy: a) a szimmetriatengely; b) a központja szimmetria? Válasz: a) Igen b) Nem

9 Hosszúkás cikloist görbe, amely leírja a ponton van rögzítve a kiterjesztése a kör sugara gördülő vonal mentén úgynevezett kiterjesztett cikloist.

11 rövidített ciklois görbét, amely leírja a ponton rögzítve a belső kör sugara mentén gördülő egyenes vonal, az úgynevezett rövidített ciklois.

13 Gyakorlat 1 Döntetlen a pálya csúcsa egy egyenlő oldalú háromszög, gurul egy egyenes vonal.

14 2. gyakorlat Döntetlen a pályáját a négyzet csúcsai, gurul egy egyenes vonal.

15 3. gyakorlat Döntetlen a pályája csúcsa egy szabályos hatszög, gurul egy egyenes vonal.

16 1 kardioid röppályáját egy pont rögzített kerületi gördülési a külső oldalon a másik kör ugyanolyan sugarú nevezzük kardioid. Válasz: a) a Nyugat; b) East; at) keleti d) délre; d) észak felé; e) délre; g) északra. A képes kardioid osztja a kört egyenlő részre a 8. pont A 1. 8 A = B. Határozza meg, ahol a bázis pont, ha a kör lesz, hengerelt a vonalon eléri pont: a) A 4; b) A 2; a) 6; g) A 1; d) A 3; e) A 5; f) A 7.

17 kardioid 2 kombinálása sima görbe ábrázolt ponttal kapjunk kardioid.

18 Kardioid mozgásban

19 1. gyakorlat e kardioid: a) a szimmetriatengely; b) a központja szimmetria? Válasz: a) Igen b) Nem

20 2. gyakorlat Draw pályájának csúcsa egy egyenlő oldalú háromszög, hengerelt a külső másik derékszögű háromszög.

21 3. gyakorlat Draw csúcsai egy négyzet pálya mozgásának gördülési a külső oldalán egy másik négyzet alakú.

22 4. gyakorlat Draw pályájának csúcsa egy szabályos hatszög, hengerelt kívülről egy másik szabályos hatszög.

23 Hosszúkás kardioid pályája egy pont rögzített kiterjesztése kör sugara mentén gördülő másik körbe ugyanolyan sugarú nevezik hosszúkás kardioid. Döntetlen a görbe.

25 Rövidített kardioid pályáját a pont rögzítve a belső kör sugara mentén gördülő másik körbe ugyanolyan sugarú, az úgynevezett rövidített kardioid. Döntetlen a görbe.

27 astroid pályája egy pont rögzítve egy kör gördülő belül egy másik körben 4-szer nagyobb sugarú, úgynevezett astroid. Döntetlen a görbe.

29 1. gyakorlat e astroid: a) a szimmetriatengely; b) a központja szimmetria? Válasz: a) Igen b) Igen.

30 2. gyakorlat Draw pályája csúcsai egy tér oldalán a mozgás 1, a gördülő a belső oldalon egy másik oldalán a tér a 4.

31 Hosszúkás astroid röppályáját egy pont fix a meghosszabbítása a kör sugarát gördülő belül egy másik körben 4-szer nagyobb sugarú, úgynevezett astroid hosszúkás. Döntetlen a görbe.

33 Steiner görbe pályája egy pont rögzítve egy kör gördülő belül egy másik körben 3-szor nagyobb sugarú, a görbe az úgynevezett Steiner. Döntetlen a görbe.

35 Steiner hosszúkás görbe pályája egy pont fix a meghosszabbítása a kör sugarát gördülő belül egy másik körben 3-szor nagyobb sugarú nevezzük Steiner hosszúkás görbe. Döntetlen a görbe.

36 A hosszú görbe Steiner

37 epiciklois görbét, amely leírja a ponton rögzítjük a kerületi gördülési a külső oldalán a másik kör, az úgynevezett epiciklois. Az arány a sugarak eltérő lehet. Döntetlen epiciklois amikor a sugarak aránya 2: 3.

39 Hosszúkás epiciklois görbét, amely leírja az a pont, rögzített a folytatása a kör sugara gördülő a külső oldalán a másik kör, az úgynevezett hosszúkás epiciklois. Az arány a sugarak eltérő lehet. Döntetlen hosszúkás epiciklois, amikor a sugarak aránya 2: 3.

41 rövidített epiciklois görbét, amely leírja az a pont, rögzített egy kör sugarát gördülő külső oldalán a másik kör, az úgynevezett rövidített epiciklois. Az arány a sugarak eltérő lehet. Döntetlen egy rövidített epiciklois, amikor a sugarak aránya 2: 3.

43 hipociklois görbét, amely leírja egy pontot rögzített egy körön gördülő belsejében egy másik kört, úgynevezett hipociklois. Az arány a sugarak eltérő lehet. Döntetlen hipociklois ha az arány a sugarak 2: 5.

45 Gyakorlat 1 Draw röppálya pont rögzített körbefutó gördülési a külső oldalán a másik kör, ha a sugarak arány 1: 2.

46 2. gyakorlat Draw röppálya pont rögzített körbefutó gördülési a külső oldalán a másik kör, ha az arány a sugarak 2: 1.

47 3. gyakorlat Draw röppálya pont rögzített körbefutó gördülési a külső oldalán a másik kör, ha az arány a sugarak 2: 5.

48 4. gyakorlat Draw pályája pont rögzített egy körön belül mozgó másik körbe kétszer nagyobb sugarú. A görbe a mozgás Válasz: A kör átmérője.

49 5. gyakorlat Igazoljuk, hogy a pálya mozgását egy pont rögzítve a kerülete a gördülő belül egy másik körön kétszer nagyobb sugár átmérője. Megoldás: Legyen a orsókoszorút költözött B ponttól D, P - a közepén. Jelöljük a metszéspont C AB kör átmérője. Ezután CPD szög kétszerese a szög BOD. Következésképpen a BD és a CD egyenlő az ívet, azaz C - pont, rögzítve a gördülő kör.