A hajlítási elmozdulások meghatározása a kezdeti paraméter módszerrel
Előadás 2.1. A hajlítási mozgások meghatározása a kezdeti paraméter módszerrel. Változó keresztmetszetű gerendák elmozdulásainak meghatározása
A hajlítási elmozdulások meghatározása a kezdeti paraméter módszerrel
Az elmozdulások meghatározása a rugalmas vonal differenciálegyenletének közvetlen beillesztésével a nagyszámú szelvényű gerendák esetében nagyszámú integrációs állandót határoz meg.
A számítási munka nagy számának csökkentése érdekében számos módszert fejlesztettek ki. A kezdeti integráció módszere szintén vonatkozik rájuk.
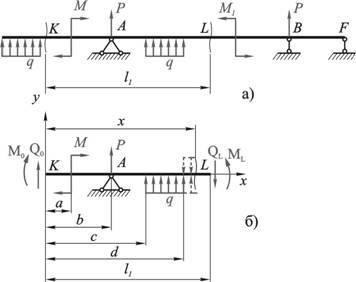
A hosszúság gerenda bizonyos részét (2.1.1. Ábra, a), a rajzszakaszokat az u. Az 1. ábrán. 2.1.1, b ezt a szegmenst mutatja, a következő leggyakrabban előforduló terhelésekkel:
a) az abszcisszában lévő keresztmetszet M koncentrált nyomatéka;
b) koncentrált erő az abszcisszal;
c) egyenletesen elosztott terhelés az abszcisszal az abszcisszal rendelkező szakaszból.
d) Ezenkívül a sugárirányú rész végein a keresztirányú erőket és a hajlítónyomatékokat alkalmazzák, és felváltják a gerendázat mentálisan eldobott részeinek hatását.
Kiválasztjuk a koordináták eredetét a vizsgált gerenda szélső szélső pontján, és általánosan meghatározzuk a gerenda összes részét.
Vonatkozunk egy tetszőleges szakaszra a származástól távol.
Az egyenletek kivezetésekor az összes terhelés irányát úgy választjuk meg, hogy pozitív hajlító pillanatokat okozzon.
A hajlítási pillanatokat a koordinátával a keresztmetszet bal oldalán lévő terhelések figyelembevételével végezzük. Amikor az egyenletekben a külső koncentrált pillanatot bevonjuk, egy tényezővel szaporítjuk. egyenlő az egységgel. Az elosztott terhelés megszakadása esetén a kérdéses szakasz végéig meghosszabbodik, és egy "kompenzáló" terhelést vezetnek be a tényleges szállítási feltételek helyreállításához. "
Az integráció a zárójelek megnyitása nélkül történik.
A koordináta szekcióhoz tartozó hajlítónyomaték kifejezést alkotjuk
Legyen egy rugalmas vonal differenciálegyenlete
Az egyenlőség mindkét oldalát integráljuk anélkül, hogy kinyitnánk a zárójeleket.
Nyilvánvaló, hogy
Következésképpen az integráció állandói és a kiindulási feltételek helyettesítése mellett megegyeznek a forgási szög és a kiindulási eltéréssel. Az elhajlás és a forgásszög a kezdeti paraméterek.
Több pillanat és erő esetén, valamint a terjesztett terhelés több részének esetében az egyenletet a következő formában kell megadni:
Ezt az egyenletet általában rugalmas vonal univerzális egyenletének nevezik.
Az eltérések univerzális egyenletének differenciálásával megkapjuk a szakaszok forgási szögeinek egyenletét
Az univerzális egyenletekben csak azokat a terheket helyezik el, amelyek a vizsgált szakasz bal oldalán helyezkednek el. A koordináták eredete a gerenda szélső bal keresztmetszete.
Így az eltolódások meghatározása a kezdeti paraméterek módszerével elsősorban az u paraméterek értékének meghatározására szolgál. amelyeket a gerenda rögzítésének körülményei határozzák meg.
Határozza meg az elosztott terheléssel betöltött konzolgerenda szabad végének keresztmetszetét (2.1.2. Ábra).
Egy adott terhelés elakadásakor reakció és reakció pillanat következik be.
Nyilvánvaló, hogy ilyen típusú rögzítés
Az univerzális egyenleteket helyettesítjük.