Kiszámítása fém fürtös
Meghatározása belső erők farm
Gyakran előfordul, hogy nincs arra lehetősége, hogy egy közönséges gerenda egy szerkezet, és van egy bonyolultabb szerkezet, az úgynevezett farm.
fém rácsos számítás, bár eltér a számítás a fényt, de nem lesz nehéz kiszámítani azt. Tőled csak akkor lesz szükség a figyelmet, az alapvető ismereteket az algebra és a geometria, és egy vagy két óra szabad ideje.
Tehát kezdjük. Mielőtt számolni a gazdaság, kérdezzük néhány valós helyzetet, amellyel szembe kerülhetnek. Például be kell zárnia a garázsban szélessége 6 méter, hossza 9 méter, de nincs padló födémek, gerendák vagy nem. Csak a fém sarkok különböző profilok. Ennek oka, hogy ezek, hogy mi lesz összegyűjteni a gazdaság!
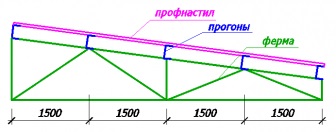
Ezt követően, a farm épít fut és teraszok. Szem gazdaságban garázs falak - csuklós.
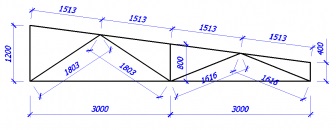
A kezdéshez meg kell tanulni az összes méretek és szögek a gazdaság. Itt van szükségünk, és a matematika - azaz a geometria. Szögeket a koszinusz tétel.
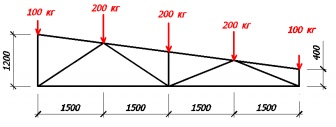
Akkor meg kell gyűjteni az összes terhet a gazdaságban (látható a cikkben kiszámítása állomány). Tegyük fel, hogy megkapja a következő lehetőséget loading:
Ezután kell felsorolni az összes elemet farm csomópontok és adja meg a referencia-reakció (az elemek be vannak jelentkezve zöld és kék komponensek).
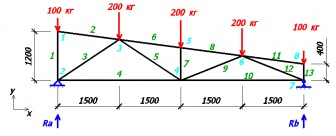
Ahhoz, hogy megtalálja a reakciók, tudjuk írni az egyenletet az egyensúly erők az y tengelyen, és az egyenlet egyensúlyi pillanatok tekintetében a 2 csomópont.
A második egyenletből találunk támogatást reakció Rb:
Rb = (200 * 1,5 + 200 * 3 + 200 * 4,5 + 100 * 6) / 6;
Rb = 400 kg
Tudva, hogy Rb = 400 kg, az első egyenletből találunk Ra:
Miután a támogatás reakciók nem ismeretesek, meg kell találni a helyszínen, ahol a legkevésbé ismeretlen mennyiségeket (mindegyik számozott tétel - egy ismeretlen mennyiség). Ettől a ponttól kezdve elkezdjük osztani a farm önálló egységek és a belső erők, hogy megtalálja farm rúd minden ilyen csomópontokat. Ez az e belső erőfeszítések, és mi felvesszük a keresztmetszet rúd.
Ha kiderült, hogy erőfeszítések irányulnak a központtól, a rúd, akkor a web hajlamos nyúlik (hogy visszatérjen az eredeti helyzetébe), aztán megszorította. És ha a rúd erőfeszítések középpontja felé irányuló, majd a rudat hajlamos összehúzódni, ami azt jelenti, van nyújtva.
Nos, nézzük számítás. Az 1 csomópont csupán 2 ismeretlenek, ezért úgy ez a csomópont (erőkifejtés irányban S1 és S2, mi kifejtette nézeteit minden esetben van a végén kiderült jobbra).
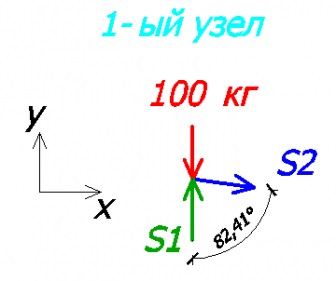
Tekintsük az egyenlet egyensúlyi az x és y tengelyen.
S2 * sin82,41 = 0; - az x tengelyen
-100 + S1 = 0; - az y-tengelyen
Az első egyenlet egyértelmű, hogy S2 = 0, azaz, a második rúd nincs betöltve!
A második egyenletből, hogy S1 = 100 kg.
Mivel az értéke S1, akkor egy pozitív, az azt jelenti, az irányt az erőfeszítéseket általunk választott helyes! Ha ez volna kiderült negatív, az irány, hogy módosítsa a jel változott „+”.
Ismerve a erő irányában S1, el tudjuk képzelni, milyen az első rúd.
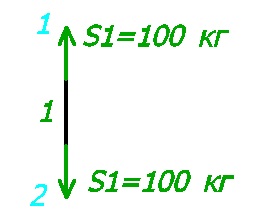
Mivel az egyik erőfeszítéseket tettek, hogy a csomópont (1 csomópont), és egy második erőt fog irányulni, hogy a csomópont (2 csomópont). Így a web próbál kinyújtom, így összenyomódik.
Ezután úgy a csomópont 2. félidőben 3 ismeretlen mennyiségeket, hanem azért, mert azt tapasztaltuk, értékét és irányát az S1, továbbra is csak 2 ismeretlenek.
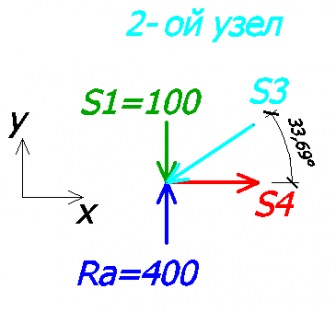
Ismét alkotunk az egyenlet az x és y tengely:
-100 + 400 - sin33,69 * S3 = 0 - az y-tengelyen
- S3 * cos33,69 + S4 = 0 - az x tengelyen
Az első egyenlet S3 = 540,83 kg (rúd №3 tömörített).
A második egyenletből S4 = 450 kg (rúd №4 feszített).
Tekintsük a nyolcadik csomópont:
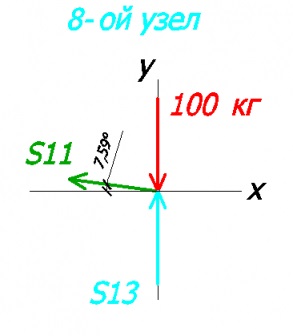
Alkotunk az egyenlet az x és y tengely:
-100 + S13 = 0 - az y-tengelyen
-S11 * cos7,59 = 0 - az x tengelyen
S13 = 100 kg (rúd №13 tömörített)
S11 = 0 (nulla mag, minden erőfeszítést az nincs jelen)
Tekintsük 7. csomópont:
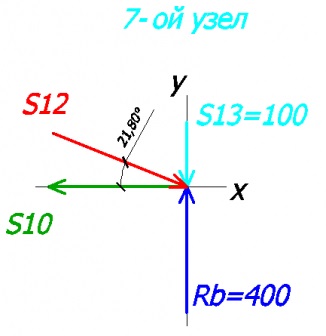
Alkotunk az egyenlet az x és y tengely:
-100 + 400 - S12 * sin21,8 = 0 - az y-tengelyen
S12 * cos21,8 + S10 = 0 - az x-tengelyen
Az első egyenletből találunk S12:
S12 = 807,82 kg (rúd №12 tömörített)
A második egyenletből találunk S10:
S10 = 750,05 kg (rúd №10 feszített)
Akkor úgy №3 csomópontot. Hogyan emlékszik a második rúd van nulla, ezért nem készít.
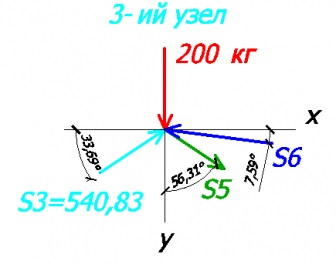
Egyenletek az x és y tengely:
-200 + 540,83 * sin33,69 - S5 * cos56,31 + S6 * sin7,59 = 0 - tengely y
540,83 * cos33,69 - S6 * cos7,59 + S5 * sin56,31 = 0 - az x-tengelyen
És itt már nem kellett algebra. Nem fogom részletesen a festék módszert találni ismeretlen mennyiség, de a lényeg - az első egyenletből kifejezni S5 és helyettesítsük a második egyenletben.
Az eredmények szerint a kapjuk:
S5 = 360,56 kg (rúd №5 feszített)
S6 = 756,64 kg (rúd №6 tömörített)
Tekintsük №6 site:
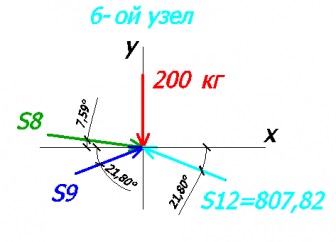
Alkotunk az egyenlet az x és y tengely:
-200 - S8 * sin7,59 + S9 * sin21,8 + 807,82 * sin21,8 = 0 - az y-tengelyen
S8 * cos7,59 + S9 * cos21,8 - 807,82 * cos21,8 = 0 - az x-tengelyen
Csakúgy, mint a 3. oldalon fogjuk találni a ismeretlen.
S8 = 756,64 kg (rúd №8 tömörített)
S9 = 0 kg (rúd №9 nulla)
Tekintsük №5 site:
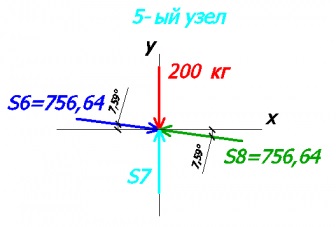
-200 + S7 - 756,64 * sin7,59 + 756,64 * sin7,59 = 0 - az y-tengelyen
756,64 * cos7,59 - 756,64 * cos7,59 = 0 - az x tengelyen
Az első egyenlet találunk S7:
S7 = 200 kg (rúd №7 tömörített)
Mivel a teszt számítások figyelembe vesszük a negyedik csomópont (erőfeszítéseket, hogy megfékezze №9 nem):
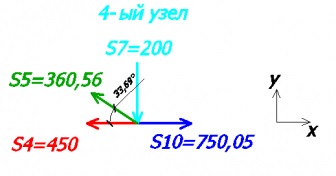
Alkotunk az egyenlet az x és y tengely:
-200 + 360,56 * sin33,69 = 0 - az y-tengelyen
-360,56 * cos33,69 - 450 + 750,05 = 0 - az x-tengelyen
Az első egyenlet kapjuk:
A második egyenletben:
Ez a hiba elfogadható, és a kapcsolódó legvalószínűbb sarkokkal (két tizedes helyett 3-ex).
Az eredmények szerint megkaptuk a következő értékeket:
Úgy döntöttem, hogy még egyszer ellenőrizze az összes számításaink a programban, és megkapta pontosan ugyanazokat az értékeket:
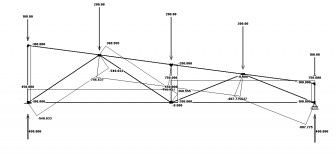
Selection részben rácsos elemek
Kiszámításánál a fém farm elvégre a belső erők a rudak talált, akkor folytassa a kiválasztási keresztmetszete a rúd.
A kényelem minden érték a táblázatban.
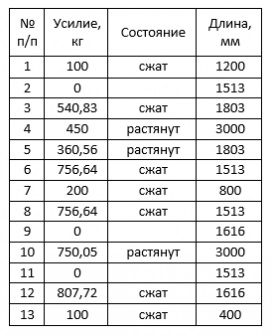
A számítások, akkor több kell, mint a tényleges hossza és a számított. A becsült hossza találunk nyissz II-23-81 * «Steel Structures”. A táblázat az alábbiak szerint:
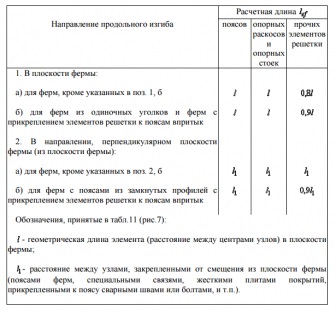
Mint látható a táblázatban, ellenőrizni fogjuk a pin gazdaságban a két irányban:
- síkjában a rácsos
- a sík a rácsos (síkjára merőleges a gazdaság)
A hossza 9 méter a garázsban rakjuk 4 traktor, 3 méter, így a geometriai kialakítása és a hossza a rúd a sík a rácsos lesz a 3 métert.
Ezután, attól függően, hogy a rudat a sűrített vagy nem, az alábbi képlet szerint számítjuk a szükséges keresztmetszeti területe.
Kiszámításánál a sajtolt magokat, használjuk a képlet (kötelező rúd terület):
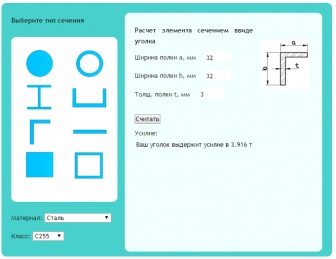
E szerint a képlet, akkor lehet számolni online számítás.
És azt is, nézze meg a web maximális rugalmasságot biztosít. Általános szabály, hogy a lehető legnagyobb rugalmasságot nem lehet több, mint a 100-150.
Amennyiben lx - a becsült hossza a síkban a gazdaság
Ly - a becsült hossza a sík rácsos
IX - mentén forgás sugara x tengely
Iy - forgási sugara az Y tengely mentén
Kiszámításánál a kifeszített rudak használjuk a következő képlet (kötelező rúd terület):
Ez a képlet használható egy online számítása húzott tagok.
Például, a két párosított zárójelben 32h3 ellenáll erő egyenlő 3,916 * 2 = 7,832 m.