harmonikus oszcillátor
Úgynevezett harmonikus oszcillátor rendszer oszcillál, a forma által leírt egyenlet (140,6):
Ingadozása a harmonikus oszcillátor egy fontos példája a periodikus mozgásra, és pontos vagy hozzávetőleges modell sok problémát a klasszikus és a kvantumfizika. Példák tavaszi harmonikus oszcillátor, matematikai és fizikai inga rezgőkör (az áram és feszültség olyan alacsony, hogy a hurkok lehet tekinteni, mint a lineáris, lásd §146.).
1. Tavaszi inga - ez egy rakás. lógott egy teljesen elasztikus tavasszal és áteső harmonikus rezgés a rugalmas erő révén F = - k x, ahol k - a rugalmassági tényező, abban az esetben a rugó nevezett merevsége. Az egyenlet a mozgás az inga
A kifejezést (142,1) és (140,1), hogy a tavaszi inga leng a törvény szerint a ciklikus frekvencia
Képlet (142,3) érvényes rugalmas hullámokkal határokon belül, amelyben a törvény Hooke (cm. (3,21)), m. E., amikor a rugó tömege kicsi képest a tömeg test.
A potenciális energia az inga rugó szerint (141,5) és (142,2) egyenlő
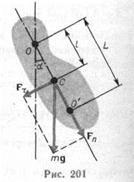
2. Fizikai inga - egy testet szilárdan összekapcsoltán a gravitációs oszcillációk körülbelül egy rögzített vízszintes tengely a felfüggesztés, amely nem halad át a tömegközéppontja C a test (ris.201).
Ha az inga eltérítés a stabil egyensúlyi helyzete egy bizonyos szögben. majd összhangban az egyenlet a dinamika a forgómozgásának egy merev test (18,3), a visszaállító erő M nyomatékot felírható
ahol - a tehetetlenségi nyomatéka az inga egy olyan tengely körül ponton áthaladó O, l - közötti távolság a felfüggesztés pontjától és a központ az inga tömege, - visszaállító erő (a mínusz jelet annak köszönhető, hogy az a tény, hogy az utasításokat, és mindig ellentétes; megfelel a kis rezgések a inga, azaz kicsi ... eltérése az inga az egyensúlyi helyzet).
Egyenlet (142,4) felírható
azonos a (142,1), amelynek megoldása (140.1) jól ismert:
A kifejezést (142,6) következik, hogy a kis rezgések fizikai inga oszcillál egy ciklikus sebességgel (lásd. (142,5)) és egy időszakban
ahol L = J / (ml) - A fizikai inga hosszának csökkenésével.
Az O pont „a kiterjesztése a OC egyenes, amelynek távolsága a felfüggesztési tengelyének a régióban adott hosszúságú L. úgynevezett fizikai inga swing Center (ábra. 201). Alkalmazva a tételt a Steiner (16,1), azt kapjuk,
t. e. OO „mindig nagyobb, mint az operációs rendszer. A felfüggesztés pontjától és a központ oszcilláció O „az a tulajdonságuk, cserélhetőség. ha a felfüggesztés tengelyének mozog a hinta közepén, a lényeg az ugyanazon a tengelyen a felfüggesztés lesz az új központ a swing és az átmeneti időszak oszcilláció fizikai inga nem fog változni.
3. Pendulum - ez idealizált rendszer, amely egy anyagi pont m tömegű. szuszpendálunk egy súlytalan nyújthatatlan izzószál és oszcilláló hatása alatt a gravitáció. Jó közelítéssel a matematikai inga egy kis nagy labdát felfüggesztve egy hosszú, vékony szál.
A tehetetlenségi nyomaték egy egyszerű inga
ahol l - hossza az inga.
Mivel a matematikai inga lehet leírni, mint egy speciális esete egy fizikai inga, feltételezve, hogy az összes tömege koncentrálódik egy ponton - a tömegközéppontja, majd helyett a kifejezés (142,8) a általános képletű (142,7), kapjuk expressziós időszakra oszcilláció a matematikai inga kis
Összehasonlítva képletek (142,7) és (142,9), azt látjuk, hogy ha az ekvivalens L hossza egyenlő a fizikai inga hossza L matematikai inga, az oszcilláció időszakok azonos. Következésképpen, a csökkent fizikai inga hossza - a hossza a matematikai inga oszcilláció időszakban, amely egybeesik azzal az időszakkal oszcilláció egy fizikai inga.