fénytörést
§ 71 fénydiffrakciós
Ha a fény hullám folyamat, valamint az interferencia kell tartani, és diffrakciós fény. Miután diffrakciós - hajlító hullámok akadály élek - velejárója minden hullámmozgás. De tartsa be a diffrakciós fény nem könnyű, mert a hullámok eltérítik a egyenes vonalú terjedését a jelölt sarkokat csak az akadályokat, amelyek mérete hasonló a hullámhossz és a fény hullámhossza, mint tudjuk, akkor nagyon kicsi.
Halad egy vékony fénysugár egy kis lyukon látható törvénysértést az egyenes vonalú terjedését a fény. egy fényes folt a képernyőn ellen a lyukak nagyobb lesz, mint a sugár méretét.
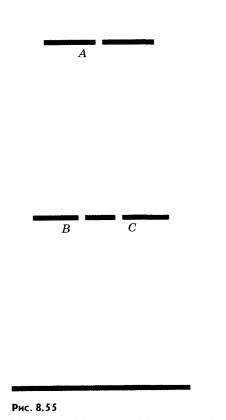
Young kísérletet. 1802-ben, T. Jung, kinyitotta az interferencia fény, a fázis egy klasszikus tapasztalat diffrakciós (ábra. 8,55). Az átlátszatlan Shearman ő áttört pin két kis nyílások B és C egy kis távolságra egymástól. Ezek a nyílások fedett keskeny fénysugár áthalad a kis kikötő A másik képernyőre. Ez az részletezésre nagyon nehéz volt kitalálni abban az időben, úgy döntöttem, hogy megtapasztalják sikert. Zavarja, mert csak koherens hullámok. Alakult összhangban Huygens elvének gömbhullám által gerjesztett lyukak Egy a nyílások B és C koherens oszcillációk. Mivel a diffrakciós a nyílásokon, és a C belőle két fénykúp, amelyek részben átfedik. Ennek eredményeként a beavatkozás két fényhullámok megjelent a képernyőn váltakozó világos és sötét csíkokkal. Zárás a nyílások egyike. Jung felfedezte, hogy az interferencia csíkok eltűnnek. Éppen ez tapasztalat először Jung hullámhosszon mértük, amely megfelel a fénysugarak különböző színű, és nagyon pontos.
Fresnel elmélete. diffrakciós vizsgálat fejeződött be a munkálatok O. Fresnel. Fresnel nemcsak részletesebb vizsgálatot különböző eseteit diffrakciós a tapasztalat, hanem kidolgozott egy kvantitatív elmélete diffrakciós, amely lehetővé teszi, elvileg ábra. 8,55 kiszámításához diffrakciós hogy mi történik a kerekítés fény minden akadályt. Ő is volt az első, hogy ismertesse az egyenes vonalú terjedését a fény egy homogén környezet alapján a hullám elmélet.
Fresnel ezeket a sikereket elérni kombinálásával Huygens elv az ötlet interferencia szekunder hullámok. Az ötlet a Fresnel egyes pontja a hullámfront van etsya forrás másodlagos hullámok, a WTO minden rendű koherens források (Huygens Fresnel elv).
Annak érdekében, hogy kiszámítható az amplitúdó a fény hullám a tér bármely pontján, szükséges, hogy a surround fényforrás mentálisan zárt felület. Interferencia hullámok a másodlagos forrásokból felületén helyezkedik el, meghatározza az amplitúdó a ponton a tér.
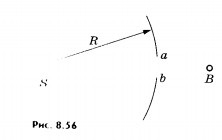
Az ilyen számítások lehetővé teszik, hogy megértsük, hogy a fény a pontforrás S, amely bocsát gömbölyű hullámokat eléri egy tetszőleges pontot a térben (ábra. 8,56).

Augustin Fresnel (1788- 1827) - francia fizikus. Azt megalapítá hullám optika. Hozzáadása az ötlet Huygens elv a beavatkozás a másodlagos hullámok, kifejlesztettem egy kvantitatív elmélete diffrakciós. Alapján ezt az elvet, hogy ismertesse a jogszabályok geometriai optika. különösen egyenes vonalú jellege a fény terjedési homogén közegben. Által létrehozott közelítő számítási módszere a diffrakciós minta alapján a hullám felületén felosztás zónák. Ez az első alkalom bizonyult a transzverzalitási fényhullámok.
Ha figyelembe vesszük a másodlagos források egy gömb alakú hullám felülete R sugarú, az eredménye beavatkozás hullámok ilyen másodlagos áramforrások B pontnál ugyanaz, mint ha csak másodlagos források kis gömb alakú szegmens AB szórja a fényt a B pontban A másodlagos hullámok által kibocsátott források elhelyezve a fennmaradó felszíni, kioltják egymást interferencia miatt. Ezért, minden úgy történik, mintha a fény szaporított a vonal mentén az SB, t. E. A egy egyenes vonal.
Alapján ez az elmélet Fresnel bizonyult egyenes vonalú terjedését a fény és a vizsgált mennyiségileg diffrakciós által különféle akadályokat.
Diffrakciós a különböző akadályokat. Által végzett számítások Fresnel teljesen megerősítette kísérletben. Annak a ténynek köszönhetően, hogy a hullámhossz nagyon kicsi, a hajlásszöge a fény a egyenes vonalú terjedési iránya kicsi. Ezért egyértelmű megfigyelése diffrakciós szükséges vagy használni nagyon kicsi az akadályokat, vagy nem rendelkeznek a képernyőn található akadályokat. Ha a távolság az akadály és a képernyő mérete nagyságrendileg méter akadály nem haladja meg a néhány század milliméter. Ha a távolság a képernyő eléri a több száz méter, vagy több kilométerre, a diffrakciós látható a méret az akadályokat néhány centiméter, vagy akár méter.
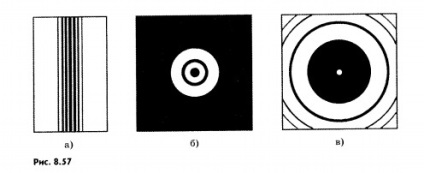
Ábrán 8,57, A-C vázlatosan szemléltetik diffrakciós mintákat a különböző akadályok: egy - egy vékony huzal; b - a kerek lyukak; in - egy kör alakú képernyőn.
Ehelyett az árnyék a huzal látható fény és sötét csíkok; a központban a diffrakciós minta a lyuk jelenik meg sötét folt körül egy világos és sötét gyűrűk 1; a központban az árnyék által alkotott kör alakú képernyőn, látható fény spot és árnyék veszi körül egy sötét koncentrikus gyűrűk.
A furcsa eset történt ülésén a Francia Tudományos Akadémia 1818-ban Az egyik tudós, aki részt vett az ülésen rámutatott arra, hogy az elmélet a Fresnel kövesse a tények nyilvánvalóan ellentétes a józan ész. Így bizonyos méretű lyukak és bizonyos távolságot a lyuk, hogy a fényforrás és a képernyő közepén a fényfolt kell lennie egy sötét folt. És egy kis átlátszatlan lemez, éppen ellenkezőleg, kell egy fényes folt a közepén az árnyékban. Mi volt a meglepetés a tudósok, amikor fel kísérletek bebizonyították, hogy, és ez tényleg!
A határértékek alkalmazhatóságának geometriai optika. Minden fizikai elméletek tükrözik a folyamatok a természetben előforduló csak kb. meghatározott határain való alkalmazhatóságának megadható bármilyen elmélet. Lehetséges, hogy alkalmazza a konkrét esetben ez az elmélet, akár nem, nem csak attól függ a pontosság, amennyiben ez az elmélet, hanem az a fajta precizitás szükséges megoldani egy konkrét gyakorlati probléma. A határértékek alkalmazhatóságának az elmélet csak akkor lehet megállapítani, miután kifejlesztett egy általános elmélet, amely magában foglalja az azonos jelenségek.
Mindezek általános rendelkezések alkalmazandók geometriai optika. Ez az elmélet hozzávetőleges. Ő nem tudja megmagyarázni, például a jelenség az interferencia és a diffrakció a fény. Egy általánosabb és pontosabb a hullám optika elmélete. Szerint neki, a törvény az egyenes vonalú terjedése a fény és más jogszabályok geometriai optika végzik kellő pontossággal liph az esetben, ha a mérete az akadályokat az utat a fény sokkal nagyobb, mint a fény hullámhossza. De az biztos, hogy nem fut soha.
Változtatásával az átmérője a furat 1, akkor lehetséges a központ a diffrakciós mintát, és fényes folt körülvéve sötét és világos gyűrűk.
Action optikai műszerek által leírt jogszabályok geometriai optika. Ezek szerint a törvények alapján különböztethetők meg mikroszkóp tetszőlegesen kis részleteit egy tárgy; egy távcső, meg tudjuk állapítani, hogy létezik a két csillag bármilyen kis szögletes köztük lévő távolságot. A valóságban azonban ez nem így van, és csak a hullám elmélet a fény lehetővé teszi, hogy megértsék az oka a határ a felbontóképessége az optikai eszközök.
A felbontóképessége a mikroszkóp és a teleszkóp. A hullám fény természete korlátozza annak lehetőségét, hogy megkülönböztesse a részleteket a tárgy vagy egy nagyon kis tárgyak amikor mikroszkóppal. Diffrakciós nem teszi lehetővé, így tiszta képeket a kis tárgyak, mint a fénysugár nem feltétlenül egyenes, de hajlik a tárgyak körül. Emiatt a kép életlen. Ez akkor fordul elő, amikor a lineáris méretei tárgyak kisebb, mint a fény hullámhossza.
Diffrakciós is korlátozza a felbontás a távcső. Mivel a diffrakciós hullámok szélén a felni a lencse a kép egy csillag nem ez a lényeg, és a rendszer a világos és sötét gyűrűk. Ha két csillag egy kis szögletes távolságra egymástól, ezek a gyűrűk kerülnek egymásra, és a szem nem tudja megkülönböztetni, hogy van két pont a fény, vagy egy. Korlátozása közötti szögtávolság a világító pont, amelyen meg lehet különböztetni, aránya határozza meg, a hullámhossz, hogy az átmérője a lencse.
Ez a példa azt mutatja, hogy a diffrakciós számolni mindig minden akadályt. Ez nagyon gondos megfigyelést nem elhanyagolható akadályok esetén, amelynek méretei sokkal nagyobb, mint a hullámhossz.
Diffrakciós fény a korlátját határozza alkalmazhatóságának geometriai optika. Hajlítása fénysorompók korlátozza a felbontás a legfontosabb optikai eszközök - teleszkóp és mikroszkóp alatt.
1. Mi az a jelenség, az úgynevezett diffrakciós!
2. Miért van a diffrakciós a hullámok mechanikus óra könnyebb, mint a diffrakciós fény!
3. Miért mikroszkóp nem látja az atom!
4. Egyes esetekben a közelítés érvényes jogszabályok geometriai optika!
Tankönyvek minden tantárgyból letölthető. fejlesztése óravázlatokat a tanárok, a fizika és a csillagászat 11 osztályok online
Ha javításokat és javaslatokat a leckét, kérjük lépjen kapcsolatba velünk.
Ha azt szeretnénk, hogy a többi beállítást és javaslatokat órák, nézd meg itt - Oktatási fórum.