Lineáris műveleteket vektorok, analitikus geometria
Az összeg a + b két a és b vektorok egy olyan vektor, amely megy az elejétől a végéig, a vektor és a b vektor, azzal a megkötéssel, hogy a b vektor csatlakozik a végén egy vektor (általában egy háromszög) építése összeg + b ábrán látható. 42.
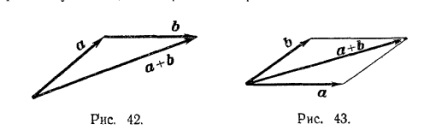
Amellett, hogy a háromszög szabály gyakran használják (egyenértékű azt). paralelogramma szabály: Ha a vektorok a és b értékét a közös eredet és építettek egy paralelogramma, akkor az összeg a + b egy vektor, amely egybeesik egy átlós e paralelogramma terjedő közös eredetű, és a és b (43. ábra). Ez azonnal azt jelenti, hogy a + b = b + a.
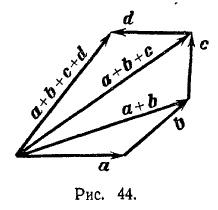
Hozzáadása sok vektorok segítségével történik egymást követő alkalmazásra háromszög szabály (lásd. Ábra. 44, ami azt mutatja, az építkezés egy összege négy vektorok a, b, c, d).
A különbség egy - b két a és b vektorok egy vektor, amely az az összeg, és NE a b vektor egy vektor. Ha a két a és b vektorok kapnak a közös eredetű, a különbség a - b a vektoros végétől terjed b ( „kivonunk”), és a végén ( „kisebbítendő”). Két vektor egyenlő hosszúságú, amelyek ellen egy egyenes vonal, és irányított ellentétes irányban, az úgynevezett kölcsönösen inverz: ha egyikük meg van jelölve egy, a másik jelöli s. Könnyen belátható, hogy a - b = a + (- b). Így, az építkezés egyenértékű azzal, mintha a különbség „csökkenti” a vektor inverz „kivonjuk”.
A terméket ohm (vagy is Aa) vektorba, és a számot α egy vektor, amelynek modulusa van a termék egy egységet vektor az egység az α; ez párhuzamos és jogok, vagy egy egyenes vonal, és irányított, valamint vektor egy, ha α - számos pozitív és ellenkező vektort és, ha a α - negatív szám.
Hozzáadása vektorok és szorzás egy vektor nevezett szám a lineáris műveletek alatt vektorok.
Megvan a következő két alapvető tétel a nyúlványok a vektorok:
1. A vetítés a vektor összeg bármely tengely összegével egyenlő az előrejelzéseket az ugyanazon a tengelyen:
2. Amikor egy vektorát megszorozzuk egy szám szorozva a vetítés „, és ugyanazt a számot:
Különösen, ha
Ha a = (X; Y; Z), tetszőleges számú α
Vektor feküdt ugyanabban a sorban vagy párhuzamos vonal, az úgynevezett esik. A jel kollinearitása két vektor
az arányosság származási helyük:
Trojka vektorok i, j, k nevezzük koordináta alapján, ha ezek a vektorok megfelelnek a következő feltételeknek:
1) vektor i fekszik az x tengelyen vektor i - az y-tengelyen vektor k - az Oz tengelyen;
2) az egyes vektorok i, j, k, hogy a tengelye van irányítva, pozitív irányban;
3) A vektorok i, j, k - egyes szám, azaz | i | .. = 1, | j | = 1, | k | = 1
Bármi legyen is a vektor és ez mindig felbontható a bázis i, j, k, azaz felírható ..:
ez a hőtágulási együtthatók a koordinátái a vektor egy (t. e. X, Y, Z jelentése a nyúlványok a vektor egy koordináta-tengely).
761. Az a és b vektorok építeni egyes alábbi vektorok: 1) a + b; 2) a - b; 3) b - és; 4) -a - b.
762. Dana: | a | = 13, | b | = 19 és | a + b | = 24. Számítsuk | a - b |.
763. Dana: | a | = 11, | b | = 23 és | a - b | = 30. Adjuk | a + b |.
764. Az a és b vektorok merőlegesek egymásra, a | a | = 5 és | b | = 12. definiálása | a + b | és | a - b |.
765. Az a és b vektorok formában szöget φ = 60 °, ahol a | a | = 5 és | b | = 8. Adjuk | a + b | és | a - b |.
766. Az a és b vektorok formában szöget φ = 120 °, ahol a | a | = 3 és 6 | = 5. Adjuk | a + b | és | a - b |.
767. Mely feltételeket kell teljesítenie az a és b vektorok, lezajlott a következő összefüggéseket: 1) | a + b | = | A - b |; 2) | a + b |> | a-b |; 3) | a + b |