forgástest
Előadás a leckét
Jobb körhenger nevezzük a test által alkotott forgása egy téglalap kb oldalán.
Következő hívjuk a test henger.
A henger által alkotott forgás AOO1 A1 négyszög körül az oldalsó OO1. Ezt nevezik a forgástengely (henger tengelye) és egy a henger magasságát. henger alap - egyenlő körök, rendezett párhuzamos síkokban. A magasság a henger nevezzük közötti távolság a síkok annak alapjait. Összekötő szakasz alapkörökön merőleges síkok a bázisok, a henger nevezzük (ez, például, a szegmensek A1 A. M1 M. B1 B. N1 N). Minden generátorok párhuzamos a forgástengellyel, és ugyanazt a hossza megegyezik a magassága a hengerben. henger sugara az úgynevezett sugara a bázis. Tengelyirányú metszete a henger nevezzük a henger keresztmetszete áthaladó sík forgástengely. Minden tengelyirányú metszetét a palack - egyenlő téglalapok (ez például, téglalapok ABB1 A1 és MNN1 M1).
A tartalmazó síkra alkotó, és merőleges az axiális átmenő metszetben, azt hívják a érintő sík a henger. A alkotója a henger forgási tengely körül határozza meg az oldalsó (hengeres) a henger felületében.
Ábra. 5.2 ábra a leolvasó henger. Scan henger felületi oldalon egy téglalap oldalai H és C, ahol H - a magassága a henger, és a C - a hossza a alapkör.
Itt képletek kiszámításához az oldalsó területen Sb és Sn teljes felületén
Jobb körkörös kúp kialakított test egy téglalap alakú háromszög körüli forgása a lábát.
Továbbá, egy köralakú kúp egyszerűen nevezhető kúp.
Cone által alkotott forgása egy téglalap alakú háromszög POA körül láb PO, az úgynevezett tengelye a kúp, P az úgynevezett csúcs. A O középpontú kör és a sugár OA az úgynevezett alap a kúp. Összekötő szakasz a csúcsát a kúp - egy pont az úgynevezett alapkör a kúp. Ábra. 5.3 szegmensek PA, PB, PM, PN - generátorok a kúp. A sugara az alap a kúp nevezzük a kúp sugara. A kúp magassága nevezzük merőleges esett a a kúp csúcsánál a tövénél. Axial szakasz egy része a kúp, a kúp által áthaladó sík a magasság.
Síkban, amely az alkotója a kúp és a merőleges az axiális átmenő metszetben az alkotója a kúp nevezzük érintőleges sík. Amikor forgó generátor PA körül van kialakítva az oldalirányú tengely PO (kúpos) felületén a kúp.
Scan az oldalsó felületének a kúp egy körcikk.
Jelöljük Sb és Sn sorrendjében, és a teljes terület az oldalsó felületének a kúp, ahol - az a szög, a felső szkennelési. Továbbá megjegyezzük, hogy. Következésképpen, ahol R - sugara, és az L - kónuszos kialakítású;
csonka
Csonka kúp része a kúp által határolt egy bázis és annak részben, olyan síkban, amely az alappal párhuzamos síkban.
A fényképek és a magassága a csonka kúp gyakran képződnek, és a magassága a teljes kúp.
Az oldalsó felülete csonka kúp megtalálható a következő képlettel: Sb = (R + R) L, ahol R és R - sugara a bázis, L - alakítás egy kúp.
Teljes felület adja meg: Sn = (R + RL + R 2 + R 2).
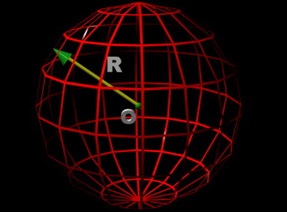
A készlet minden pontot a térben, egymástól egyenlő távolságra egy távolság R ponttól O. Ezt nevezik a gömböt.
Sphere kijelölt: (O, R). Lehetőség van körének meghatározása, és a test által alkotott forgás kör körül az átmérője.
A készlet minden pontot a térben távoli, hogy az O pont az a távolság nem nagyobb, R. nevezett el.
Más szóval, a labda - társulás szféra és az összes belső pontja.
Az is lehetséges, hogy meghatározza a labdát, és a test által alkotott forgás körüli tartományban az átmérője.
A labda is nevezik egy gömb: (O, R). Point O nevezzük központ gömb (labda). Szegmens összekötő a központ a gömb bármely ponton az úgynevezett a gömb sugarának (labda). Összekötő szakasz bármely két pont a gömb, úgynevezett akkord gömb (labda). Előfordul, hogy egy sugár vagy akkord jelenti hosszuk. Akkord középpontján átmenő a gömb nevezzük az átmérője.
T1. Ha a távolság a központtól a gömb síkjával kisebb a gömb sugara, a vonalszakasz körének ez a sík - egy kört.
A tétel, hogy ha a távolság a központtól a labdát, és a gép kevesebb, mint a sugár a labda része a sík - egy kört. Ha a repülőgép eltávolítjuk a gömb középpontjában olyan távolságra R. Ezt nevezik a érintősík.
T2. Kasatlnaya síkban egy gömb egy közös pont (érintési pont), és merőleges a sugár végre, hogy az érintési pont.
T3. Sík, egyenlő távolságra a gömb középpontja, a határokon is egyenlő körök.
Ez abból a tényből következik, hogy, ahol R - a sugara a metszésvonala.
Egyértelmű, hogy a legnagyobb kör van kialakítva a kereszteződés egy átmenő sík a gömb középpontján. A metszésvonala nevezzük nagy kört a gömb. (A megfelelő rész az úgynevezett nagy kört a labda a labda).
Húzott vonal ponton keresztül merőleges a gömb sugarának, végzett ezen a ponton az úgynevezett húzott érintő a területen.
T4. Az érintő vonal van a hatálya a körét egyetlen közös pont.
Keresztül bármely pontján a gömb fér végtelen számú érintők, amelyek mind hazugság az érintő sík.
Legyen O (a; b, c) - a gömb központ egy derékszögű koordináta-rendszerben, R - a gömb sugara, A (x; y; z) - tetszőleges pont a gömb. (Lásd koordinálja a 8. fejezetben) Majd
Megvan a gömb egyenlet O középpontú (a; b, c), és a sugara R.
Különösen, ha a központ a gömb az eredete, van az x 2 + y 2 + z 2 = R 2.
Megjegyezzük, hogy a labdát kap a következő egyenlőtlenség