Fizmatika 406

V. fejezet koordináta módszerrel az űrben. § 1. koordinátáit a koordinátákat a vektor. → száma 406

Tekintsük az általános eset. Tekintsünk két nem egy síkba eső vektorok AB és DC. DC transzfer vektor párhuzamosan úgy, hogy a kezdődő pont D1 egybeesik azzal a ponttal, a végén az első vektor. D1C1 így a vektor, vagy ami ugyanaz, BC1 vektor codirectional DC vektor egyenlő vele hosszúságú. Szerint a vektor szabályból:

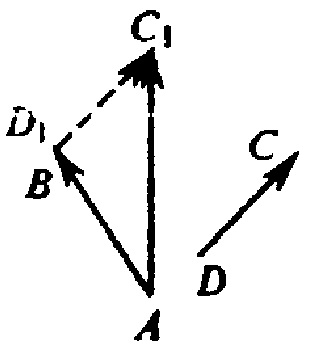
Ennek bizonyítására fejezzük koordinátáit ezen vektorok koordinátáinak

Kezdő és záró.

A kijelölés AB vektor koordinátái az x1, y1, Z1 és BC1 vektort x2, y2, z2, megkapjuk

Összegek koordináták X1 + X2, Y1 + Y2, Z1 + Z2 jelentése a koordinátáit a vektor AC1 összegével egyezik meg a két kiindulási vektorok AB és DC. QED.

← 407. Tekintettel a vektorok a, b, c és d<— 2,7; 3,1; 0,5>. Find a koordinátáit a vektorok: a) a + b; b) a + c; a) b + c; g) d + b; d) d + a; e) a + b + c; f) b + a + d; h) a + b + c + d