diéderes Wikipedia
Hópehely van Dih6 diéderes szimmetria, az ugyanaz, mint a szabályos hatszög.
Diédercsoport (torziós) - a szimmetria csoport egy szabályos sokszög. beleértve mind a forgatást. és axiális szimmetria [1]. Diédercsoport a legegyszerűbb példa a véges csoportok és fontos szerepet játszanak a csoportok elmélete. geometria és a kémia. Ez jól ismert, és teljesen triviális, hogy ellenőrizze, hogy a csoportot, amelyet két involúció véges elemek számát a definíció a diédercsoport.
Elnevezések [| ]
Két alaptípusa felvétel diédercsoport társított n -storonnim poligon. A geometriában egy csoport kerül rögzítésre Dn. míg általában algebra, az azonos csoportba nevezzük D2n. használva indexeként az elemek száma a csoportban. Van is egy Coxeter jelölést. ahol tengelyszimmetrikus jelöljük [n] (körülbelül 2n), és a forgó mind a [n] + (n rend). Újabb rekord - orbifolds jelöléssel. amelyben az axiális szimmetria jelöli * nn. és forgatás - mind az N.
Ebben a cikkben, Dn (vagy néha, Dihn) utal, hogy a szimmetria egy szabályos n-gon.
Definíció [| ]
Elements [| ]
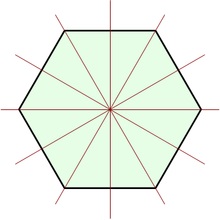
Hat axiális gondolatok szabályos hatszög
Szabályos n-szög 2n különböző szimmetriák: n forgatás és n reflexiók tengelyen. alkotó diédercsoport Dn. Ha n páratlan, minden szimmetriatengelye áthalad a közepén az egyik oldalon, és a szemközti csúcs. Ha n páros, van N / 2 szimmetriatengellyel összekötő felezőpontja szemközti oldalán és n / 2 tengely összekötő szemközti csúcsa. Mindenesetre, van szimmetriatengellyel n és 2n elemek szimmetria csoport. Reflection képest egy tengely, majd a másikhoz képest forog kétszer közötti szög a tengelyek. Az alábbi képek mutatják az eredményt a D8 tag közúti jel megálló:

Az első sor mutatja a nyolc forgatások, és a második - nyolc reflexiók.
A szerkezet a [| ]
Mint minden más geometriai objektumot, a kompozíció két szimmetriák egy szabályos sokszög ismét szimmetrikus. Így a szimmetria egy szabályos sokszög alkotnak véges csoport.
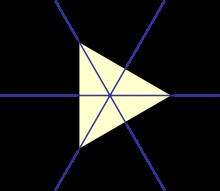
Diédercsoport a csoportja a szimmetria 2D és a csoport a forgatások 3D [| ]
Egy példa egy absztrakt csoport Dihn és hagyományos módon van egy csoport grafikai predstavleniyat Dn síkban isometries. Ne mozgassa a származás. Ezek a csoportok alkotják a két sorozat diszkrét csoportok pont a síkon. Dn áll n forgatások egy szög többszöröse 360 ° / n. az origó körül, és n reflexiók relatív tengely középpontján áthaladó koordináta és a szög a fennmaradó a tengelyeket, amelyek többszörösei 180 ° / n. Ezek a pontok jelentik a szimmetria csoport egy szabályos sokszög N oldala (n ≥ 3).
Diédercsoport Dn generálja forgása érdekében n r és s reflexió körülbelül 2, oly módon, hogy
Ami a geometria: egy tükörkép forgatás néz ki, mint egy balra forgás.
Ami a mátrixok: beállítás
Diédercsoport D2 r forgása által előállított 180 fokkal, és a szimmetriatengely ek tekintetében: X. A elemeket D2 lehet kifejezni, mint az e, r, s, rs>, ahol e - személyazonosító átalakítás és rs - szimmetria tengelyhez képest Y.
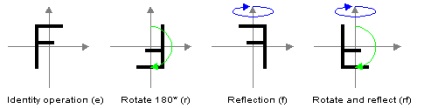
Négy elemek D2 (X jelentése egy függőleges tengely)
Az n> 2 a forgatás és a reflexió működés tekintetében a közvetlen nem kommutatív és Dn nem Abel. Például, a D4. forgatás 90 fokkal, majd a mérlegelés ad egy nagyon más eredményt, mint a gondolkodás és megforgatjuk.
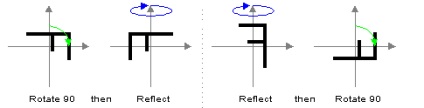
D4 nem Abel (X tengely függőleges).
Így, valamint a nyilvánvaló alkalmazási problémákhoz szimmetriasíkjában, ezek a csoportok az egyszerű példák a nem-Abel-csoport, és gyakran használják a counter-példákat tételek korlátozott Abel-csoportok.
2n Dn elemek felírható e. r. R 2, ..., rn -1. s. R s. r 2 s, ..., rn -1 s. Az első N-ezen elemek forgatások, a maradék n - képest a tengelye reflexió (mindegyik rend 2). Az eredmény két forgás vagy két reflexiók lesz forgatva a forgatás és reflexió lesz tükrözi.
Azonban, Dn megjelölést használják SO (3) az alcsoportok. amelyek szintén Dihn típusú csoportok. csoport szimmetria sokszög ágyazott háromdimenziós térben (ha n ≥ 3). Ezek a számok lehet tekinteni, mint degenerált test (innen a név diedron (diéder „).
Példák kétdimenziós szimmetria diedralov [| ]
Egyenértékű definíciók [| ]
Dihn következő meghatározásokat ekvivalensek:
- gráfautomorfizmus csoport áll csak egy ciklus n csúcsú (ha n ≥ 3).
- ábrázolását a csoport
Tulajdonságok [| ]
Tulajdonságok Dihn diédercsoport n ≥ 3 függ a paritás n. Például, Dihn központ a csoport az csak a személyazonosságát a páratlan n. és két elem még, nevezetesen, a identitás és rn / 2
Ha m osztója n. Dihn van a n / m Dihm formában alcsoportok. és egy alcsoport Zm. Így a teljes száma alcsoportok Dihn csoport (n ≥ 1) d (n) + σ (n), ahol d (n) - a számos természetes és n osztója σ (n) - az összeg a természetes osztója n.
Konjugáltsági osztály reflexiók [| ]
Minden páronkénti konjugátum reflexió esetében a páratlan n. de azok nem esnek két conjugacy osztályok még n. Ami a izomorfizmus helyes -gons n: páratlan n bármely két reflexiók is képviselteti magát forgatás, míg a még n csak a fele a reflexiók lehet beszerezni egy rotációs fordul. Egy geometriai szempontból, az egyes poligon a páratlan szimmetriatengely áthalad az egyik csúcsot és központja az ellenkező oldalon, és a még ott van két tengely, minden egyes készlet az osztályukhoz konjugáció - a tengely átnyúlik a csúcsa és egy átmenő tengely felezőpontja az oldalán.
Algebrai, akkor a képviselők az konjugáltsági a Sylow tétel. páratlan n bármely reflexiós együtt neutrális elem egy rendű alcsoport 2, amely 2-Sylow alcsoport (2 = 2 1> - maximális teljesítménye két, elosztjuk a 2 n = 2 (2 k + 1)), míg a még n . Ezek alcsoportok 2-rendű nem Sylow, mint 4 (legnagyobb teljesítmény két) osztja a sorrendben a csoport.
Az n páros helyett, van egy külső automorfizmus. kétféle reflexiók átültető.
automorfizmus csoportja [| ]
Ez lehet érteni reflexió és a generátor elemi forgások (forgatás a K (2 # X03C0; / N). k elsődleges, hogy n). Mi a belső automor, és néhány kívül függ a paritása n.
- A páratlan n diédercsoport nincs középpontja, úgy, hogy minden elemet határoz meg, nem-triviális belső automor. Az n is 180 ° -ban forgatható (reflexió a középpontjának koordinátáit) nem triviális Center eleme.
- Így, páratlan n. belső automor csoport rend 2n, és egy még - a sorrendben n.
- A páratlan n. minden visszaverődések konjugátum, még azok két osztályba sorolhatók (azok, amelyek áthaladnak a két csúcs, és azok, akik átmennek a felezőpontja az oldalak), és ezek a két osztály van társítva egy külső automorfizmus, ami lehet például a forgási # X03C0; / N (a fele a minimális elfordulási szög).
- Forgatás így normális részcsoport. visszaverődés konjugáció megváltoztatja a jel (irány) a forgatás, de egyébként nem változnak. Automorfizmusa megszorozzuk szögek k (vzamnoprostoe hogy n) a külső, kivéve, ha k = # X00B1; 1.
Példák a csoportok automorfizmusok [| ]
Dih9 18 rendelkezik belső automorfizmusok. Ahogy isometry csoport kétdimenziós térben, D9 van egy reflexió időközzel 20 °. 18 automorfizmusok belső reflexiók, hogy forgási számú többszöröse 20 °, és a reflexió. Ahogy izometrikus csoportot azok automorfizmami. Van még, amellett, 36 külső automorfizmusok. például úgy, hogy megszorozzuk a forgatási szög 2.
Generics [| ]
Számos fontos általánosítása diédercsoport:
- Végtelen diédercsoport - egy végtelen sávban egy algebrai szerkezete hasonló a szerkezete a diéderes végcsoportok. Meg lehet tekinteni, mint egy szimmetria számok csoportját.
- Ortogonális csoport O (2), vagyis a kört szimmetria-csoport. Azt tulajdonságai hasonlóak a tulajdonságai véges diédercsoport
- A család az általánosított diédercsoport tartalmazza a fent bővítése, valamint még sokan mások.
- Kvaziedralnye csoport - egy család végcsoportjai vannak tulajdonságai hasonlóak a tulajdonságai a végső diédercsoport.
Lásd még [. | ]
Megjegyzések [| ]
Irodalom [| ]
Javítani ezt a cikket matematika kívánatos: