Topológikus mátrix - studopediya
Alapvető gráfelméleti alapfogalmak
Topológiai LEÍRÁS RENDSZEREK
Alatt egy matematikai modellt, hogy megértsék a sor leíró egyenletek áramköri megoldást, amely lehetővé teszi, hogy meghatározza annak jellemzőit. Matematikai modellek általában végre lineáris rendszerek nemlineáris algebrai vagy differenciálegyenletek. A módszer kialakítására matematikai modell áramkörök halmaza topológiai és alkatrész egyenletek.
Áramköri topológia kényelmes leírni a nyelv gráfelmélet, amelynek több mérnöki alkalmazások. A topológia az áramkör hordoz kapcsolatot információs elemeket. Topológiai áramkör egyenletek olyan formája felvétel fő topológiai törvényeket (az első és második törvényei Kirchhoff). Komponens egyenletek képviselik felvétel Ohm törvénye, hogy az alkatrészek - az áramköri elemeket.
Ahhoz, hogy leírják a áramköri topológia, mindegyik bipoláris elem helyébe irányított vonalszakasz, egy ága grafikon. Csatlakozó két vagy több ágra pontban nevezett egy csomópont vagy csúcsa a grafikon. Felsorolása csomópontok és ágak az elektromos áramkört és az annak megfelelő grafikon.
Megfogalmazzuk Kirchhoff törvényei áramkörök.
Kirchhoff feszültség törvény: az összeg a feszültség bármelyik mentén zártláncú hurok nulla.
Kirchhoff törvényei az áram:
1. A algebrai összege folyó áramok a csomópontot, és a kapott összeállítás nulla.
2. Minden rész, amely elválasztja az áramkör két részre, az algebrai összege átfolyó áramok ágai az összekötő szakasz nulla.
Irányai vonalszakaszok (áramok) passzív ágak lehet önkényesen választottuk, azonban egyetértenek abban, hogy az az irány egybeesik a jelenlegi források igaz és a feszültségforrás ellen irányul EDS.Uzly számozott rendszer véletlenszerűen folyamatos számsor, a teljes (a földelési pont) általában nullának tekintjük .
előfordulási mátrix. Alkalmazása Kirchhoff törvény áramok a csomópontok teszi lehetséges előfordulási mátrix, amely leképezi a topológiai tulajdonságait az áramkört. Tekintsünk egy egyszerű áramkört és annak megfelelő grafikon (2.1 ábra).
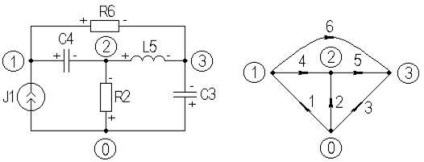
2.1 ábra - az elektromos áramkör és annak irányított gráf
Írjunk Kirchhoff törvény áramok a csomópontok:
Etiuravneniya felírható mátrix formában
ahol - előfordulása mátrix.
Ebben a példában a mátrix formájában:
A mátrix tartalmaz sorok és oszlopok, ahol - a független (földeletlen) csomópontok; - Számolja ágakat. A sorok jelzik az ágak esetet a megfelelő csomóponti és azok tájolását. Az oszlopok jelzik, csomópontok, amelyek az eset, hogy a megfelelő ágat, és a bejárási sorrendet.
Feszültség potenciálok ágak és csomópontok is keresztül kapcsolódik a mátrix esetén megfelelő arányban a Kirchhoff feszültség törvény
ahol - az előfordulási mátrix átültetés; - feszültség ágak - csomópont feszültségét.
Matrix szakaszok és kontúrok. Ábrán látható 2.2 A grafikonon az előző áramkör, de három részre. A pozitív iránya keresztmetszetek rámutatnak a nyilak.
2.2 ábra - Count a áramköri rész
Alkotunk az egyenlet a szakaszok az áram:
Felmerül a kérdés: mennyi van szükség egyenletek, és határozza meg az áram és a feszültség az áramkör? Válaszolni kell használni a koncepció fagráf.
Fa kapcsolódó gráf egy csatlakoztatott részgráf, amely magában foglalja az összes csomópontban, de nem tartalmaz hurkot. Az ágak nem szerepelnek a grafikonon fa, így egy komplementer gráf fa. Fagráf lánc () csomópontok van ágak. Az ágak a grafikon tartalmazza a fa, az úgynevezett élek. Ágak komplementer gráf nevezzük akkordokat.
A fő rész a grafikon hívják metszete egyik szélét, és tetszőleges számú akkordokat. mert csak egy része a fa ágai, van egy fő-keresztmetszet, amely megfelel a független egyenletek az áramlatok.
A számozás az ágak, valamint az alkatrészek egy tetszőleges eljárás és szempontok szabják meg, a kényelem. Sok számítások jelentősen egyszerűsíthető, ha:
1) válasszuk irányban ágak;
2) Válassza ki a fa a gráf;
3) címke az ágakat a grafikon, első borda, akkor a húrt.
2.3 ábra mutatja, az egyik megvalósítási mód szerint egy ilyen választás. Egyenlete a szakaszok az aktuális ebben az esetben a következő lesz:
2.3 ábra - Graph rendszerek egy dedikált fa
A mátrix formában ezeket egyenletek írhatók, mint