-Származékok és a mátrix, a problémamegoldás a matematika és egyéb tárgyak

Találunk meghatározó a kapott mátrix.

# 8710; 3 = (-1) 1 + 1a11 # 8710; 11 + (-1) 2 + 1a21 # 8710; 21 + (-1) 3 + 1a31 # 8710; 31 = 16 • (3 • (-28) - (- 1) • 44) -10 • (2 • (-28) - (- 1) • (-14)) + 6 • (2 • 44-3 • (-14)) = 840

Írjunk külön talált változók X

B) a fordított mátrixba.

Jelöli egy - mátrix együtthatók az ismeretlen; X - oszlop mátrixa ismeretlenek; B - oszlop mátrixa abszolút értelemben :, vektor B: BT = (- 14,44, -28)

Ezekkel elnevezések, az egyenletrendszert veszi a következő mátrix forma: A · X = B.

Ha A - nem-degenerált (determinánsa nem nulla, akkor van egy inverz mátrixot A-1 szorzása mindkét oldalán az egyenlet az A-1, megkapjuk az A-1 * A * X = A-1 * Szoba, A-1 *. A = E.

Ez az egyenlet az úgynevezett mátrix formában oldatot egy lineáris egyenletrendszer. Ahhoz, hogy megtalálja a megoldást egyenletek kiszámításához szükséges az inverz mátrix A-1.

A rendszernek van egy megoldás, ha a meghatározója a mátrix nem nulla.

Mi található a fő meghatározója.

Így a meghatározó 140 ≠ 0, ezért továbbra is megoldást. Ehhez találunk az inverz mátrixa cofactors.

Tegyük fel, hogy egy nem-szinguláris mátrix:

Ahol Aij - kofaktor a meghatározó eleme aij A mátrix, amely a termék a (-1) i + j a Minor (determináns) N-1 érdekében, kapott deléciós I-edik sorának és a j-edik oszlop a meghatározója a mátrix A.

Transzponált mátrixszal Egy a formája:

Kiszámoljuk az cofactors.

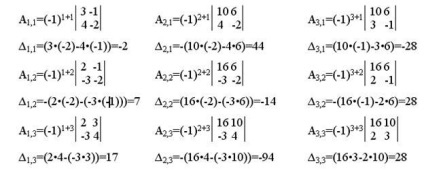
Ezekből kofaktorok alkotják a csatlakozómodulok mátrixot:

Kiszámítjuk az inverz mátrix:

Vektor eredmények X X = A-1 • B