Megtalálása integráló tényező - studopediya
A meghatározása integráló tényező, van
vagy, elosztjuk két oldalán (10,20) a,
Kaptunk formájában (10,20) és (10.20) egy parciális differenciálegyenlet a funkciója ismeretlen. A probléma az integráló ez az egyenlet általában nem könnyebb, mint a probléma megoldása az egyenletnek (10.6). Természetesen tudnunk kell, hogy csak egy bizonyos egyenlet megoldása (10,20), néha néhány jellemzője az egyenlet (10,20), lehet találni egy adott megoldást, majd az integráció az egyenlet (10,6) csökkenti kvadratikus.
Például, vegyük azt az esetet, ahol van egy integráló tényező, amely az X függvényében csak.
Ebben az esetben, = 0, és egyenlet (10,20 „) van felrajzolva egy ilyen
Egyértelmű, hogy a létezése integráló tényező, amely nem függ az szükséges és elégséges, hogy a jobb oldali rész egy funkciója x, akkor Area:
Példa 10,6: (2xy + x 2 + y) dx + (x 2 + y 2) dy = 0
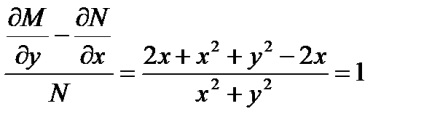
Ennélfogva, = 1, = x, x = e
vannak rendes differenciálegyenlet. Integrálni,
Megtalálására (y) kiszámítja és egyenlővé N
és az általános integrálját az egyenletnek
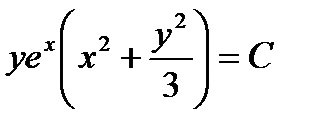
Tekintsük a konkrét esetben egy integráló tényező, amely attól függ, csak x, ahol N = 1 ebben az esetben, az egyenlet a forma
Egyenlet (10.21) formáját ölti
azzal a feltétellel. amely az X függvényében.
Ebben az esetben, az f (x, y) a formája
azaz egyenlet írásos formában (10,22), és amely lehetővé teszi az integráló tényező, amely attól függ, csak x lineáris egyenlet.
Egyenlet (10,21), van
A jelölést a 9. fejezetben a lineáris egyenlet, eljutunk a következtetést.
A lineáris egyenlet integráló tényező
Primer10.7: Az egyenlet egy integráló
tényező. megszorozzuk mindkét oldalán, mi van
ahol a bal oldalon egy teljes eltérés, integráló lelet