A sztochasztikus rezonancia jelenség nemlineáris rendszerek - studopediya
A „sztochasztikus folyamat” egy olyan régiót jelent a káosz, hogy a kaotikus viselkedés a folyamat, a dinamikája, amely véletlenszerű és kiszámíthatatlan. Egy ismert példa egy ilyen folyamat a Brown-mozgás.
A „rezonancia” a legáltalánosabb értelemben egy erős választ a rendszer a kis külső befolyás. Fontos, hogy egy ilyen erős választ - szelektív, vagyis csak akkor, amikor bizonyos paraméterek a külső befolyást. Resonance akkor jelentkezik, ha a frekvenciát a külső hatás, mint a természetes frekvenciája oszcilláció a rendszerben.
Együtt a két szó jelent nagyon érdekes, és első pillantásra, ellentétben a józan ész, a jelenség, amely számos, nagyon különböző rendszerek, sőt, mint kiderült, már régóta használják a természet.
Ezt a jelenséget fedezte fel a 80-as években. A lényege sztochasztikus rezonancia abban a tényben rejlik, hogy ha a zajt a rendszerben, azaz kaotikus mozgás nem csökkenti, hanem növeli a rendszer válasza a gyenge periodikus hatása. Ebben az esetben, a zaj nem csak elnyomja a jelet, hanem segít, hogy megnyilvánuljon. A legerősebb hatás akkor jelentkezik, amikor egy jól meghatározott, az optimális zaj intenzitása.
Bárki, aki szembesült a szelekciós problémát a hasznos jelet a zajtól, egyértelműnek tűnik, nyilatkozat arról, hogy az első lépés ebben a folyamatban a lehető legnagyobb zajcsökkentés intenzitását. Mivel az idő hajnalán rádió, amikor a mérnökök először hallotta a sziszegő jött hangszórók, ők keresik a módját, hogy elnyomja a zajt, hogy óhatatlanul bekövetkező elektromos áramkörök és kommunikációs rendszerek. Úgy véljük, hogy létrehoz a zaj csak akkor szükséges, olyan helyzetekben, amikor azt szeretnénk, hogy nem ad valaki megbízható, hogy a kívánt jelet.
Az ötletet, hogy az a zaj, hogy javítsa a jel minőségét abszurdnak tűnik, mert minden normális ember gondolná, például karcolás a CD, hogy olvassa el az információkat jobb lett belőle. Azonban a legújabb kutatások azt mutatják, hogy bizonyos esetekben zaj konstruktív szerepet játszik a megítélése gyenge jelek hatására, az úgynevezett „sztochasztikus rezonancia”. A jelenség annyira szokatlan, hogy az első alkalommal megnyitása után, felkeltette a figyelmét egy nagyon korlátozott a tudósok, főleg azok, akik azt és úgy találta.
Sztochasztikus rezonancia - periodikus jel erősítés mellett fajlagos teljesítménye fehér zaj. Ez egy univerzális jelenség, amely számos nemlineáris rendszerek külső hatás ugyanakkor kaotikus és gyenge periodikus hatása.
Ahhoz, hogy ezt a jelenséget, hogy bármely bistabil rendszer disszipáció, súrlódás. Befolyása alatt elegendő külső befolyás ilyen rendszer átmehet egy másik állam. Ha elegendő külső fellépés időközönként, a rendszer, valamint, időről időre át az egyik állapotból a másikba. Elégtelen (tudatalatti) expozíció nem okoz a rendszer válaszát. Ha a külső hatások véletlenszerűen (zaj), a rendszer véletlenszerűen „vándorlás”, és miután határozatlan időre, az átlagos hossza függ a zaj ereje tud ugrani az egyik helyzetből a másikba. A dinamika ilyen ugrások rendetlen.
Nézzük a halmozott hatását küszöbérték alatti periodikus és kaotikus hatásokat. Maga küszöb alatti rendszeres zavarása nem lesz képes átadni a rendszert egy másik állam, de a zaj teszi ezt összeadásával expozíció a „kritikus” állapotban van. Ennek eredményeként, a válasz a rendszer látható periodicitással által meghatározott gyenge periodikus erő.
Optimális (ami a maximális jel-zaj arány), hogy a zaj teljesítménye, ahol a jellemző a rendszer élettartama ugyanolyan állapotban felével egyenlő az időszak az periodikus zavar. Túl erős vagy túl gyenge zaj vezet kevésbé érzékeny a rendszer gyenge periodikus akció.
A feltétel az esemény sztochasztikus rezonancia - a rendszer nem lineáris, vagy a rendszer válaszát a nettó hatás egyszerűen az összeg a válaszokat, és nem vezet új hatásokat.
A rendszernek legalább két stabil vagy metastabil állapotok. Ez lehet egy bistabil rendszer és a rendszer a hosszú élettartamú metastabil gerjesztett állapot.
Azoknál a rendszereknél, amelyek bemutatják sztochasztikus rezonancia, többek között, mint például: a dinamika jégkorszakok a Földön; Észak-atlanti éghajlat dinamikájára; pumpáló egy gyűrű lézer; Érzem számos állat.
Vegyük például, bármely bistabil rendszerben. A „bistabil rendszer” - egy rendszer két helyzete stabil egyensúlyi állapotot. Egyszerű mechanikai például - a mozgás egy részecske a potenciális két minimumot (ld. 1.). Ha a részecske járt még, és a súrlódási erő, egyértelmű, hogy nem számít, hogy mit választunk kezdeti feltételek, ingadozások a végén, kihal, a részecske „bukása” az egyik potenciális kutak, és ott marad a végtelenségig.
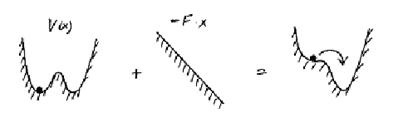
Ábra. 14.6 példa viselkedés bistabil rendszer külső hatással rajta.
Ahhoz, hogy a részecske mindig van egy másik potenciális jól, szükséges csatolni egy külső erő. Ha ez az erő elég nagy, akkor a „pull” részecske az első is, és el fog terjedni ez a második. Az esetleges nyelvi (ebben a szövegben, a potenciális szinonimájaként használják a potenciális energia) „gyakoroljon külső erő” azt jelenti, hogy adjunk lineárisan növekvő potenciál ábrán látható. 14b. Ha V (x) - bistabil potenciális, egy külső erő meghaladja az értéket = | V „(x) |, hozott az inflexiós pont, azaz, ahol a visszaállító erő által létrehozott potenciál a legnagyobb. Ezután a teljes lehetséges módosítva van az ábrán látható módon, és a részecske csúszik a második lyukba. Ha a külső erő időszakos időben, ennek következtében a részecske lesz „ugrás” egy jól másikra, majd vissza. Ennek eredményeként, a billenő rendszer reagál erős külső hatás. A gyakoriság, amellyel a rendszer ugrik át egyik stabil állapotból a másikba, ugyanaz, mint a frekvenciát a külső visszacsatolás. Ha a külső hatás nagyon erős, akkor a rendszer engedelmesen ismételni a változások és ingadozások az erő. Ha a külső hatás nem lesz olyan erős, azaz a <, то частица не сможет покинуть яму и останется в ней, несмотря на внешнее воздействие.
Így a bistabil rendszer egy bizonyos érzékenységi küszöb: ha a külső erő> rendszer kezd ugrani az egyik állapotból a másikba frekvencián a külső erő, és amikor <система не чувствует внешнее воздействие. То есть, у бистабильной системы существует некий порог чувствительности к внешним воздействиям. Слишком слабые, т.е. подпороговые воздействия остаются для системы незамеченными, но при дополнительном воздействии на такую систему, даже стохастическим сигналом может происходить усиление сверхслабых сигналов.
Ábra. 14,7 jelek a) és azok Fourier transzformálja b).
A sztochasztikus természete jel véletlenszerű zaj. Fourier-transzformációs periodikus jel lehet elválasztani a zaj.
Figyelembe véve a bistabil rendszer hatása alatt a véletlen teljesítmény ingadozások fog bekövetkezni véletlen. Ebben az esetben előfordulhat, hogy egy részecske kóborol egy potenciál is, és hirtelen ugrás a második. Nyilvánvaló, hogy minél több zaj, annál kevesebb ideig ugráló, azaz annál a részecske ugrik egyik üregből a másikba. Ha képviseli a függőség a koordinátáit a részecskék mire lehet megkerülni egy ilyen képet, amint az ábra. 14.8.
Ábra. 14.8 Rendszer válasz a véletlen külső befolyást.
Ha egy külső zaj és egy gyenge add, küszöbérték alatti periodikus jelet, akkor a részecskék továbbra is kihagyja egyik üregből a másikba, de a természete ennek a folyamatnak változik: periodikus komponens jelenik meg abban foglalt időtartamával megegyező időszakra a külső jel gyenge. Azaz, az ugrások végzi véletlenszerű erő, és az, hogy időnként „moduláló” hatás (vagyis hozzáadja a saját frekvencia).
A hang egy korábban leküzdhetetlen akadályt távolít el egy potenciális és az okozza a rendszert, hogy tudatalatti jelet.
Ez a lényege a sztochasztikus rezonancia (amplifikáció). Sztochasztikus rezonancia jellemzője az, hogy van egy bizonyos optimális zaj intenzitása, amely a választ a rendszer periodikus a legerősebb jelet. Annak érdekében, hogy meghatározzák, milyen nagy ez a válasz, meg kell rajzolni a koordinátákat egy részecske az idő, és a Fourier-transzformáció, hogy jelöljenek ki egy periodikus jel komponens. Ezután az amplitúdó a kiegészítő „púp” a Fourier-transzformáció (ábra. 14,7) fog szolgálni a mennyiségi jellemző a rendszer érzékenysége. Minél magasabb a púp, annál erősebb a jel a külső periodikus mozgás egy részecske.
Ábra. 14.9 válasz bistabil rendszer különböző intenzitású zaj.
Az ábra azt mutatja, hogyan függ a koordinátáit a részecske idő egy és ugyanazon gyenge periodikus jel, de eltérő intenzitással zaj. Úgy látszik, hogy ha a zaj intenzitása alacsony, a részecske egy hosszú ideje az egyik lehetséges is, mielőtt ugrik egy másik (ábra. 14,9, alsó grafikon). Külső órajel nem ölt itt. Amikor intenzitásának növelésével zajt optimális részecske összesített hatása alatt a zaj és egy periodikus erő szinkron hop egyik üregből a másik (ábra. 14,9, középső panel). Jól látható periodikus komponens rendszer reagálása, a időszak, amely egybeesik azzal az időszakkal, a külső erő. Végül, további fokozására a zaj, részecskék mozgásának egyre szabálytalan; periodikus komponensek a válasz csökken (ábra. 14,9, felső diagram),.
Egy tipikus rendszer reagálása függését az intenzitás a külső zaj ábrán látható. 14.10. Úgy látszik, hogy egy bizonyos intenzitású zaj a rendszer válaszát a hasznos jel maximális lesz.
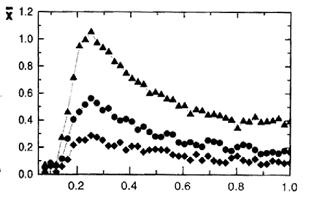
Ábra. 14.10 Az időszakos komponens jelének amplitúdójának zajintenzitásától függ.
A határozott zajintenzitás megfelel egy nagyon specifikus, az egyik lyukról a másikra való ugrásra. Az optimális zajintenzitás feltétele: szükséges, hogy az e zaj által okozott ugróidő egyenlő legyen a gyenge periodikus perturbáció időszakának felével. Ha a komlódási periódus és a külső erő periódusa szinkronizálódik, akkor a rendszer legerősebb reakciója egy külső periódusos perturbációnak (rezonancia) történik. Ha ez a két folyamat nem szinkronizálódik, csökken a gyengén periodikus erő iránti érzékenység.
A sztochasztikus rezonanciát a technológia használják, megfigyelve az élő szervezetek működésében. Például sztochasztikus rezonanciát alkalmaznak az optikai rendszerekben és idegimpulzusok keletkezésekor fordulnak elő.
A sztochasztikus rezonancia megfigyelésére szolgáló optikai rendszer egy példája az úgynevezett gyűrűs lézer (ábra), amelyben a lézerfényt három vagy több tükörrel rendelkező rezonátorban pumpálják. Ebben a rendszerben a lézerfény szivattyúzásának két stabil módja van, amikor a fény az óramutató járásával megegyező vagy az óramutató járásával ellentétes irányban mozog. Ez volt az első kísérlet (1988), amikor sztochasztikus rezonancia figyelhető meg a laboratóriumban.
A 90-es évek elején felismerték, hogy a sztochasztikus rezonancia kulcsfontosságú szerepet játszhat a neurofiziológiai folyamatokban, nevezetesen a neurális hálózatok működésében, az impulzusok átvitelében az egyik neuroncsoportból a másikba.
Egészen a közelmúltban, az 1990-es évek második felében felmerült a kérdés, hogy létezik-e sztochasztikus rezonancia a kvantum szintjén. Várható, hogy a kvantum "részecske rázása", amely mindig is abszolút nulla hőmérsékleten van, és amely itt játssza a zaj szerepét, megkönnyíti a kvantumjel feltárását, az információk terjesztését stb.
Sztochasztikus rezonancia is előfordulhat olyan rendszereknél, amelyek nem bistabil rezonanciák. A fő követelmény a küszöb jelenléte. Egy ilyen rendszerre példa egy olyan rendszer, amelyben nem ugrál fel két stabil egyensúlyi helyzet között, hanem a rendszer "alap" és "izgatott" állapota között.
A közelmúltban leírtak egy "kettős sztochasztikus rezonancia" jelenséget. Itt kétféle zaj zajlik a szabad részecske egyszerre: az első valami olyasmit hoz létre, mint egy bistabil potenciál, a második pedig a részecsket ugrik ezen a pszeudopotenciálon. A jelenség nagyon érdekes, mert kiválóan illusztrálja azt a tényt, hogy a zaj nemcsak a finom, korrelált folyamatokat elpusztíthatja, hanem éppen ellenkezőleg - életet adhat nekik.
Érdekes, hogy a közeljövőben, amikor a szubsztanciájú elektronika elhagyja a tudományos laboratóriumokat, és elérhető lesz a tömeges felhasználó számára, a sztochasztikus rezonancia fontos része lehet.
Egy másik példa a neurális hálózatok - elektronikus eszközök, amelyek képesek hatalmas mennyiségű információ hatékony feldolgozására. Az ilyen hálózatokban a sztochasztikus rezonancia a zajos információ továbbfejlesztett vezetőképessége és a hálózatok különböző részeiben egyszerre előforduló folyamatok szinkronizálása formájában nyilvánul meg.
Az utóbbi években számos jelentés jelent meg a sztochasztikus rezonancia sikeres használatában a jelfeldolgozás és a számítógépes képfelismerés terén.
Vissza a tartalomjegyzékhez: Modern alap- és alkalmazott kutatás az eszközgyártásban