Téglatest coaching
Az elméleti vázlat egy négyszögletes paralellelepipede: a tanulás a matematika középiskolai diákok és felkészülni a vizsgára.
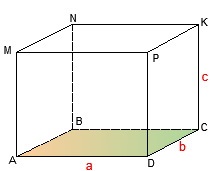
Tulajdonságok egy derékszögű paralelepipedon, amelynek hossza a, b szélesség és a magasság c:
1) Minden aspektusát - téglalapok. Szemben arcok - egyforma négyzetekre.
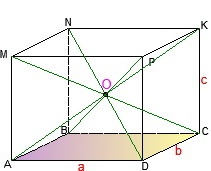
3) A metszéspontja az átlók a központja a gömb leírt
4) A tér AK átlója egy derékszögű paralelepipedon (lásd. Ábra) egyenlő a négyzetgyökét négyzetének összege hosszának annak méreteit, azaz a
Bizonyítás. Vegyünk egy derékszögű háromszög AKC. By teoerme Püthagorasz (lásd. Az alábbi ábrát). Most a háromszög ADC :. Azt kell illeszteni az első egyenletben, ahelyett, hogy a jobb oldalán az utóbbi.
5) Az összeg minden egy derékszögű paralelepipedon egyenlő a termék hosszának annak méreteit, azaz a
6) A területet a oldalfelület S = 2ab + 2BC + 2ac
8) Az ingatlan a kocka átlós átlós MC kocka ABCDMNKP- merőleges síkok (ANP) és (KBD)
- ezek a síkok van osztva három egyenlő szegmensek: MQ = QE = EK
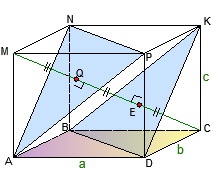
Piggy feladatok tutor matematika paralleleped
1) egy bázis oldalán egy derékszögű paralelepipedon, és egyenlő 4cm. Átlós alacsonyabb oldallapja szöget. Keresse meg a doboz magasságát.
2) nagysága derékszögű paralelepipedon, és egyenlő szöget zárnak be a két szomszédos keresztirányú széle. Mennyiségének meghatározása a doboz.
3) A kocka. Keresse MN, ha a szélén a kocka egyenlő.
Megjegyzés tutor matematika: ha kényelmetlen számítástechnikai szám, így azt tanácsolom, hogy vegye igénybe tutori matematika hasonlóság vétel. A probléma megoldásához egyes bordák megfelelő méretű, például 2 cm-es, majd megszorozzuk a kapott válasz
4) Az a kocka. Keresse MN, ha a szélén a kocka egyenlő
5) A derékszögű paralelepipedon ABCDEFGH AB = 6 cm, BC = 8 cm-es. Közepén keresztül az oldalak AD és CD, és a felső F végzett síkban szögben a sík a bázis. Keresse meg a teljes felületén a doboz.
6) A derékszögű paralelepipedon ABCDTKLP: AB = 3 cm, BC = 4cm. KD keresztül átlós a téglatest párhuzamos AC átló síkban végzett. Határozzuk meg a bezárt szög ezen a síkon, és az alapsík, ha a rendelkezésre álló térfogatot téglatest cc
7) derékszögű paralelepipedon ABCDSQPE: AB = 6m, AD = 3m, AS = 4m. Pont M, N és K megoszlanak oldalélei a paralelepipedon olyan, hogy AM: MB = 1: 1, SN: NQ = 5: 1, EK: KP = 1: 2. Számítsuk ki a terület annak keresztmetszeti síkjában MNK.
8) A derékszögű paralelepipedon ABCDFESQ: AB = 3m, AD = 10m, AF = 4m. A pontokat M, N és K megosztására oldalsó szélek a szegmensek úgy, hogy AM: MD = 1: 4, FN: NQ = 2: 3, EK: KS = 1: 2. Számítsuk keresztmetszeti terület által alkotott síkkal MNK.
Alexander Kolpakov,
matematika tanár Moszkvában. Tanítás itt Strogino
Te, persze, jól sikerült. És mit tud a legjobb terveket a lineáris programozásban?
Nem vagyok edző lineáris programozás, de van egy ötlete, a szimplex algoritmus és egy közlekedési problémát. Saját profil - klasszikus matematika, iskolai matematika, felkészülés a vizsgára és GIA. Bár az elmúlt évben segítette a régi diák beiratkozott a Pénzügyi Akadémia egy lineáris programozás. De nem megy bele ...