Tárgy 16 reális gázok
Kezdjük tömöríteni gáz miközben a hőmérsékletet állandó, bármely pont A. izotermyAV ága (mindkét ábrán) megfelel a sűrített gázt kis nyomáson. Az ingatlan a gáz a uchastkeAV nagyon közel van a ideális gáz tulajdonságaira. Amikor elér egy bizonyos davleniyaR0 gáz viselkedése drámaian megváltozik.
Gáz továbbra összehúzódni, térfogata csökken, és a nyomás ugyanaz marad (ábra. 16.3) egyenlő P0. UchastokVS naeksperimentalnoy izoterma megfelel a cseppfolyósítási folyamatba, azaz a uchastkeVS gázt átalakulnak folyékony (Sun - kondenzációs vonal). Ebben a régióban az anyag létezik egyidejűleg két fázist eredményez: egy folyékony - az egyik fázis és a második fázis - gáz, amely ebben az esetben a telített gőz folyadékhoz képest. A telített gőznyomás függ csak a hőmérséklettől, de független a térfogata. Ezért davlenieR0 nem változik mindaddig, amíg az összes gőz egy adott hőmérsékleten, nem tudja átadni a folyadékba. DavlenieP0 nazyvaetsyauprugostyu telített gőz az adott AT hőmérséklet. A lényeg az összes anyag még mindig a gáz halmazállapotú a ponton az összes anyag már folyékony állapotban.
Branch az izoterma diabétesz (mindkettő izotermák) jellemzik a folyadék kompressziós folyamatot. Folyadékok kismértékben összenyomható, így krivayaSD meredeken emelkedik.
Telek VEteoreticheskoy izoterma Van der Waals erők lehet kísérletileg kapott. UchastokVE harakterizuetperesyschenny párokat. azaz gőz, amelynek sűrűsége nagyobb, mint a sűrűsége telített gőz egy adott hőmérsékleten. State of túltelített gőz - instabil állapotban. A gőz lecsapódik könnyen része áthalad a folyékony, majd a maradék gőz van egy telített gőz.
Telek SFteoreticheskoy izoterma Van der Waals erők is kísérletileg kapott. Ez jellemzi sostoyanierastyanutoy instabil folyadékok. azaz folyadék kisebb sűrűségű, mint az szükséges, hogy ezen a hőmérsékleten. Ezt a folyadékot kapunk, ha gondosan megtisztított minden szennyeződést.
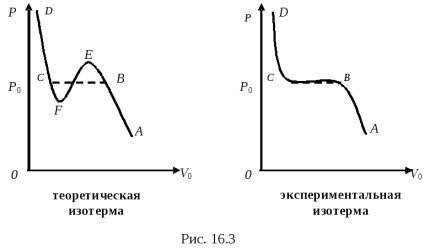
Telek FEteoreticheskoy izotermák Van der Waals erők nem lehet kísérletileg kapott.
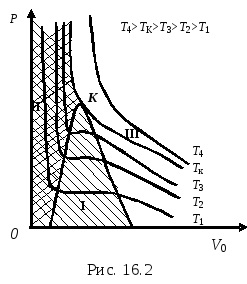
Minden egyes kísérleti izoterma valamelyikének felel meg, a hőmérséklet T = const. Növekvő hőmérséklettel, az egyenes részek a megfelelő izotermák válnak keskenyebb és egy bizonyos ponton temperatureTk Isa. korlátozza az egyenes szakasz, egyesíti egy tochkuK. Izoterm, amely kondenzációs vonal képviseli, mint egy pont, kritikus izoterma. A megfelelő hőmérséklet a kritikus izoterma - temperaturaTk kritikus. Isotherm megfelelő kritikus temperatureTk. Ez csak peregibaK pontot. TochkeK párhuzamos a érintőleges az x-tengely. Izotermák hőmérsékleten vysheTk nincs maximumok vagy minimumok nem egyenes szakaszok, közel az ideális gáz izotermák.
K pont a kritikus tochkoy.Tk. megfelelő eyPk IVK úgynevezett kritikus hőmérséklet, nyomás és a térfogat sootvetstvenno.Kriticheskoy temperaturoyTknazyvaetsya hőmérséklet, amelynél nincs különbség a folyékony és gáznemű halmazállapot. A különböző anyagok kritikus temperaturaTk más. A halmazállapot kritikus hőmérséklet az úgynevezett kritikus halmazállapot. Ebben az állapotban az anyag szerez speciális tulajdonságokkal, például elhalványul kohéziós erők a molekulák közötti, az anyag nem rendelkezik felületi feszültség, stb
Alatti hőmérsékleten a kritikus anyag létezhet függően a nyomás vagy a folyékony vagy gáznemű állapotban, vagy egy kétfázisú állapotban (folyadék és annak gőz egyidejűleg).
Fölötti hőmérsékleten a kritikus hőmérséklet egy anyag létezhet csak gázállapotban, és tömörítés nélkül nem lehet lefordítani egy folyékony állapotban. A gáz kell hűteni, mielőtt az első TTk. majd tömöríteni.
A kritikus halmazállapot megfelel egy pont a kritikus izoterma - az a pont, ahol kondenzációs vonalon fejlődött. Ez a pont az úgynevezett kritikus. Paraméterek anyagot a kritikus pontot nevezzük kritikus paramétereket. Ezeket meghatározni, szükséges megállapítani a helyzet a kritikus pont a koordináta sík P, V.
Bármilyen izoterma Van der Waals erők, beleértve a kritikus, által leírt egyenlettel
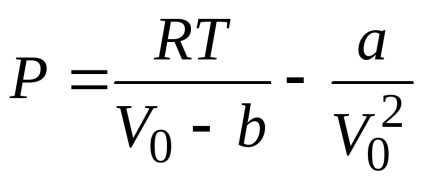
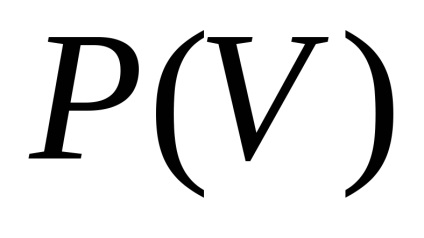
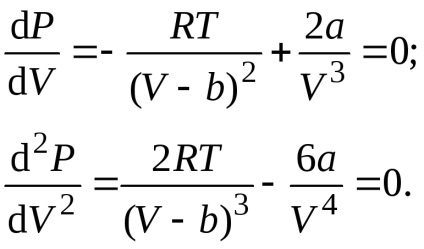
Egyenletek megoldására együtt megtaláljuk a kritikus paraméterek:
ahol a, b - állandók az egyenlet van der Waals erők, amelyek leírják egy állam egy igazi gáz, R - egyetemes gázállandó. Ábra oblasti (árnyékolt) - ez a domain kétfázisú állapotban anyag oblastII (dupla vonalkázás) - az a terület, a folyékony állapotban, oblastIII (nem árnyékolt) - egy olyan terület gáz halmazállapotú.