Poisson-tényező
Eszközök és tartozékok: a fém henger, a folyadék manométer kompresszort.
Célkitűzés: A kísérleti meghatározása az adiabatikus index
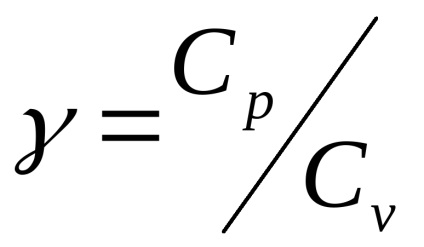
2.1. Az elméleti rész
Jellemzésére termikus tulajdonságainak a gáz, valamint bármely más szerv is különleges értéket - hő.
A hőkapacitása a test nevezzük azt a hőmennyiséget, amely szükséges felhívni rá, vagy kivonjuk azt, hogy változtassa meg hőmérséklet 1 K:
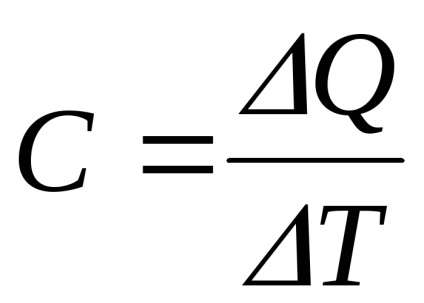
A hőkapacitás egységnyi anyag tömege, az úgynevezett fajlagos hőkapacitása. Nyilvánvalóan nem jellemezték a testet, és az anyag, amelyből a szervezet tagjai. Hő-kapacitás, említett egy mól az anyag az úgynevezett moláris hőkapacitás.
Között a fajhő - c és moláris - C létezik egy nyilvánvaló összefüggés:
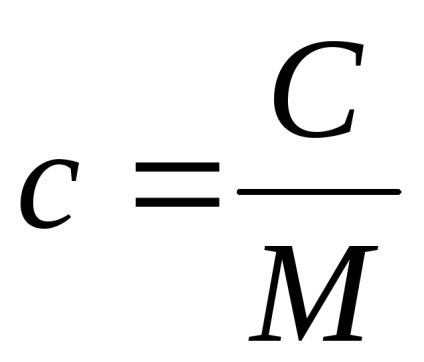
ahol M - moláris tömege (mért kg / mol).
A hőkapacitása a gáz feltételeitől függ a fűtés. Különösen, a gáz lehet melegítjük állandó térfogatú V és állandó nyomás P. Ennek megfelelően a fajlagos hő állandó térfogaton Cv és a fajhő állandó nyomáson Cp.
Az arány a Cp / Cv = γ egy olyan paraméter, az adiabatikus folyamatok és a folyamatok hozzájuk hasonló (y nevezik Poisson-tényező).
A folyamatot nevezik adiabatikus, ha ebben a folyamatban nincs gázcsere a környezettel (a falak szigetelt edény). Ha adiabatikus folyamat egy egyensúlyi (minden egyes alkalommal, amikor a P nyomás és T hőmérséklet van egyenlő a teljes mennyisége), le van írva, a Poisson-egyenlet
Az első főtétele
ahol ΔQ - a hőmennyiség átadódik a gáz, Au - változás a belső energia a gáz, AA - az elvégzett munkát a gáz a külső szervek által.
Tekintsük egy mól gáz. Ha V = const. A AA = 0, és ezért, Cv = Au /? T. Ha P = const. A AA = RΔV = RΔT. mint az állapotegyenlet (PV = RT) érvényes a kezdeti és a végső állapotban a gáz.
.
Így, moláris hőkapacitás cp és cv egy ideális gáz rokonságban
ahol R - egyetemes gázállandó.
Cp> Cv. mivel V = const teljes gáz hőt közlünk az csak a változás belső energiája a gáz, míg ha P = const Gázfűtés elkerülhetetlenül kíséri annak meghosszabbítását. Amikor a gáz működik, amely tájékoztatja őt a további hőmennyiséget.
A molekuláris gázok kinetikus elméletét azt mutatja, hogy
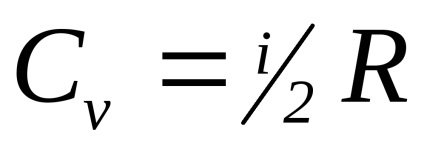
Az egyatomos molekulák i = 3 (például, nemesgázok), két atomi merev molekula (a távolság a molekulák folyamatosan) i = 5.
Hogy az ilyen molekulák N2 és O2 a levegőben szobahőmérsékleten hőmérsékleten, és ennek következtében azok
.
2.2. Meghatározási módszere a Poisson-tényező
Vegyünk egy ballon levegővel, a lezárt dugattyút és kapcsoljuk a U-alakú folyékony nyomásmérő (2.1 ábra).
1. Tegyük fel, hogy kezdetben a levegő hőmérséklete a hengerben egyenlő szobahőmérsékletre, és a légköri nyomás meghaladja egy kis mennyiségű P”. A állapotegyenlet levegő a tartályban a formája
ahol P - a légköri nyomás; T - abszolút hőmérséklete a gáz, ami megegyezik a környezeti hőmérsékleten; V - által elfoglalt térfogat levegő; P „- további nyomást (határozza meg a nyomásmérő), m - levegő tömege a hengerben, M - moláris tömege levegő (nitrogén és oxigén keverék).
2. mozgassa a dugattyút felfelé. A levegő a hengerben kitágul és lehűl. Leállítása dugattyú (V2 helyzetben), amikor a henger nyomása válik azonos az atmoszférikus (folyadék szintje mindkét lábán a manométer egyenlő). A táguló gáz nem működik, és lehűtjük.
Leállítása után a levegő dugattyú a hengerben melegítjük szobahőmérsékletre (miatt hőcsere a környezetet). ahol a nyomás a hengerben növekszik egy bizonyos érték P „(P” <Р'). Уравнение состояния воздуха в баллоне теперь имеет вид
Kiemeljük, hogy a levegő tömegét a hengerben az államokban az 1. és 2. azonosak.
3. Ebben a cikkben lényeges jellegét pneumatikus munkahenger átmenet állapotában 1. 2. állapotban, nevezetesen, ha a levegő expanziós igen gyorsan bekövetkezik, a változás a belső energia lényegesen magasabb, mint az energia, amely elmarad az idő, hogy áthaladjon a henger falán a környezettől és az expanziós folyamat lehet tekinteni adiabatikus. Ha a levegő a ballonban expanziós folyamat egy egyensúlyi (nyomás és hőmérséklet azonos az egész mennyiség), akkor egy ilyen eljárást ismertetnek a Poisson-egyenlet: RVγ = const. Egyértelmű, hogy ez csak akkor igaz, lassú bővülése. Ha mindkét állapot Poisson-egyenlet alkalmazható, és ezért
ahol P - a légköri nyomás.
és (2.1) és (2.2)
Összehasonlítva (2.4) és (2.5), megkapjuk
Logaritmusát véve (2,6), van
Amikor P ' «P (ahol P és” «P) használhatja a közelítés ln (1 + x) → x, ha x → 0 [, hogy segítségével a számológép, hogy amikor x ≤ 0,02 hiba cseréjekor ln (1+ x) x kevesebb, mint 1%. ebben a munkában h ≈ 0,2 m. mivel atmoszférikus nyomáson megfelel egy vízoszlop magassága h ≈ 10 m].
Az eredmény
mivel p '= ρgh', P "= ρgh". Így mérésével h”h”. Megtalálható Poisson γ.
2.3. beállítások ismertetése
A kísérleti berendezés egy fémhenger töltve levegővel, amely össze van kötve egy manométerrel és egy kompresszor.
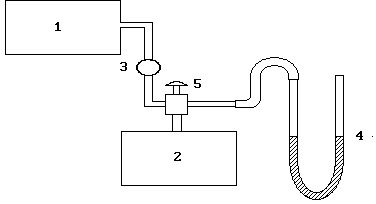
Ábra. 2.2. Fitting rendszer:
1 - kompresszor, 2 - henger, a 3 - szelep 4 - U-alakú manométer 5 - szelep
2.4. Az, hogy a teljesítmény
1. A kompresszor óvatosan felfújt ballonnal a levegőbe úgy, hogy a különbség a folyadék szintmérő lett egyenlő 25-30 cm. Zárjuk a szivattyú szelepet, hogy várjon 3-4 percig, amíg a hőmérséklet a levegő a hengerben nem egyenlő a szobában (míg a mozgást a manométer szintek ez nem fog megállni). Az alsó szinten a meniszkusz, hogy meghatározzuk folyadékszintek L1 „és L2” bármely törzsének a nyomásmérőt. Enter értékek: L1 'L2' , és H '= L1' - L2' táblázatban. 2.1.
2. A szelep A tartály csatlakoztatása a légkörbe, és tartsa nyitva, amíg a szint a nyomásmérő egyenlő. Ebben az esetben akár összehangolása minden szinten mozog az egyik oldalon. Ezt követően, zárja el a szelepet. A levegő a léggömb lesz szobahőmérsékletre melegítjük. Ennek megfelelően, a nyomás emelkedik. Miután 3-4 percig, amikor a forgalom szintje a mérőeszköz leáll, levelet értékek L1 „L2" és h»= L1«-L2” táblázatban. 2.1.
Megjegyzés. Amikor végzett kísérletben a légtömeg nem marad állandó a tartályban. Ha szivattyúzás után (1 állapot) a tömegét m1. megnyitása után a csapot a levegő jön ki a henger (állami 2), úgy, hogy a tömeg a visszamaradó levegő ott m2 Ez dlyam2 igaz az összes fenti a levezetése (2.8). Sőt, az állam 1 m2 tömege tart egy bizonyos mennyiséget V1 De 2. állapotban a tömeges m2 már elfoglalja a teljes térfogata a tartály (V2 = V. Fig.2.3). Ily módon a levegő tömegét m2 States 1 és 2 által leírt képletek (2.1) és (2.2) illetve, és az átmenet 1 → 2 - általános képletű (2,3). 3. Ismételje kísérletek legalább 10 alkalommal. A mérési eredmények, a táblázatban. 2.1. 4. A képlet szerint (2.8) kiszámításához γ minden kísérletben. 5. Számítsa ki az átlagos értéke γ. 6. A hiba meghatározására γ képlettel számítottuk ki: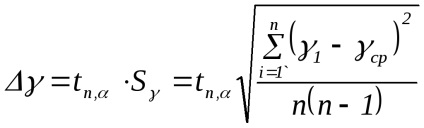
ahol
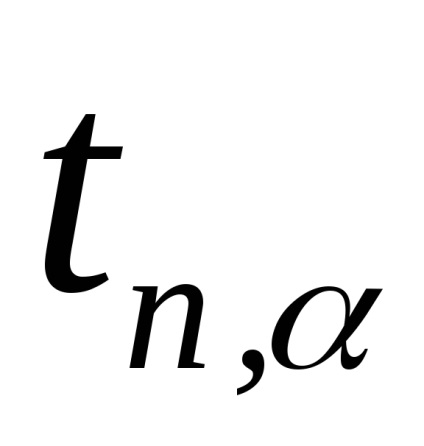
7. Hasonlítsuk össze a kapott értéket γ = γsr + Δγ γ az elméleti érték kétatomos gáz.
Által meghatározott fajlagos hőkapacitása és moláris? Mi a kapcsolat a kettő között? Mértékegységet.
Mi határozza meg a hőkapacitása a gáz?
Mi Poisson?
Mi a folyamatot nevezik adiabatikus és hogyan írták le az egyenlet?
Mi több szabadsági fokkal egy molekula?
Mi az elméleti értéke Poisson levegő?
Hogyan és miért változik a hőmérséklet és a levegő nyomása a henger alatt a tapasztalat?
Milyen hatással van az eredménye, késés, amikor a szelep zárva van K1?