Következtetések: 2. fejezet
Így keretében hullám optika, elektromágneses mező van átvezetve optikai hullámvezető a sugárzás formájában jelen lévő egy sorozat expanzió diszkrét sor sajátfüggvények hullámvezető vagy rádiófrekvenciás módok. Megfelelő jellemző funkció az ilyen típusú hullámvezető. Ezek a vegyületek előállíthatók például oldatok a Maxwell egyenletek, figyelembe véve a peremfeltételek megfelelő hullámvezető geometria. Abban az esetben, szimmetrikus sík hullámvezető módok keresztirányú villamos (TE) vagy keresztirányú mágneses (TM) sajátmódusok.
Divat szál általában hibrid (EH Ilin) hullámokat, mágneses és elektromos térerő, amelynek hosszirányú komponense. Hatékonyság gerjesztés amplitúdójának vagy üzemmódok lehet kiszámítani, mint az együtthatók a mező tágulási hullám által vezérelt sajátfüggvények. A több izgatott módok határozza meg a rádiófrekvenciás paramétert. A sík hullámvezető szimmetrikus ravno4V / . a szál -V2 / 2. Az egyes módok határfrekvenciájú hogy ilyen znachenieV. amely alatt nem tud szaporodni. Priv<1,5108 в симметричном планарном волноводе и приV<2,4048 - в волоконном остается только одна мода.
Abban az esetben, gyengén irányadó hullámvezetők leírására terjedését sugárzás lehet irányítani, hogy egy skalár megközelítés, amely jelentősen egyszerűsíti a számításokat. Ebben a divat közelítése hozzávetőleges transzverzális elektromágneses hullámok. Abban az esetben, sík hullámvezetők, az ilyen hullámok lehet kijelölni TEM módban, abban az esetben a szál - kakLP divat. A paraméterek ezeknek a hullámoknak meghatározzuk az oldat a skalár hullám egyenletet és alig különböznek a valódi paramétereit gyengén vezető hullámvezető mód.
Amikor egy skalár megközelítést figyelembe kell venni, hogy azon belül teljesen elvesztette a polarizáció változásokat vezetett sugárzás. Vegye figyelembe ezeket a változásokat lehet a megfelelő módosításokat a polarizációs fázis skalár mód paramétereit.
ellenőrzési feladatok
Célkitűzés 2.1. Egy sík hullámvezető szaporítására két sík hullámok azonos fázisban sebességgel úgy, hogy a hullám vektor egyikük orientált szögben + . és a többi- a tengellyel, amint a 16. ábrán látható. Amplitúdóinak a két hullám egyenlő, a vektorok azok elektromos mezői síkjára merőleges a rajz, és egyikük vektor

Célkitűzés 2.2. Oldja meg a problémát az előző esetben, ha a vektorok mágneses mezők a két hullám síkjára merőlegesen a rajz és elküldi a megfigyelő.
Célkitűzés 2.3. 2.1 megoldja a problémát az esetben, ha a vektorok a mágneses mezők a két hullám síkjára merőleges a rajz, és egyikük vektor
Feladat 2.4. Milyen módok is izgatott szimmetrikus sík hullámvezető Priv = 3, V = 5 és V = 8?
Célkitűzés 2.5. Az emissziós hullámhossz 1,3 mikron bevezetjük egy szimmetrikus sík hullámvezető. A törésmutatója a szál mag 1,47; héj - 1465. KakieTEM divat, hogy irányítsák az optikai szál, ha a fél-szélessége a mag egyenlő 5 mikron? 10 mikron?
Feladat 2.6. Vágás modyTEM1 szimmetrikus sík hullámvezető történik hullámhosszon 1,48 mikron. Mi lesz az üzemmód szerkezetét a hullámvezető a hullámhosszon 1,3 mikron; 1,2 mikrométer és 0,8 mikrométer?
Feladat 2.7. A törésmutatója szimmetrikus sík hullámvezető mag 1,47, a refrakciós index különbség a mag és a burkolat - 0,003. Mi kell választani félszélességére a mag hullámhosszra 1,55 mikron, ez egy egymódusú rádiófrekvenciás?
Feladat 2.8. Számoljuk ki a terjedési állandó modTEM0 ITEM1. izgatott egy sík szimmetrikus volnovodecparametrami :. n1 = 1,48; n2 = 1,46, = 50 mikron. A hullámhossz a sugárzás, hogy ravnoy1,3 mikron.
Feladat 2.9. Számoljuk ki a terjedési állandó modyTEM11. izgatott hossza volny1,3 mikron szimmetrikus sík hullámvezető paraméterek c :. n1 = 1,48; n2 = 1.477, = 5,3 mikron.
Feladat 2.10. Azt mutatják, hogy a divat lehet számítani normirovkaTEMm Vídeň =
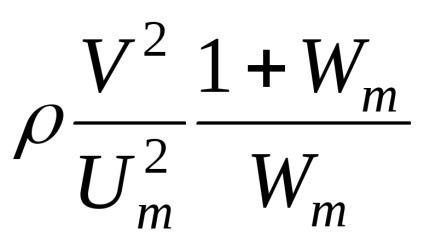
Feladat 2.11. Mutassuk meg, hogy az arány a moschnostiTEMm divat középpontjában a sík hullámvezető lehet kiszámítani
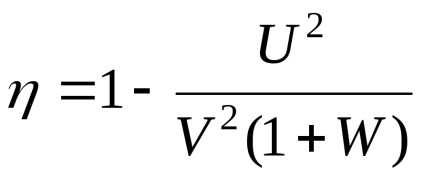
Feladat 2.12. Igazoljuk, hogy az összteljesítmény elkülönített sík hullámvezető hullámhossz lehet kiszámítani kakP = PX + PN. GDEPT =
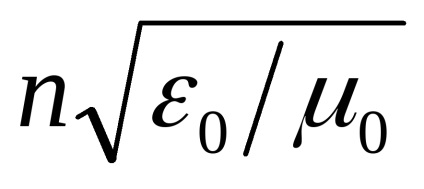
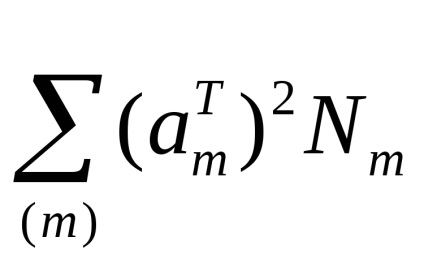
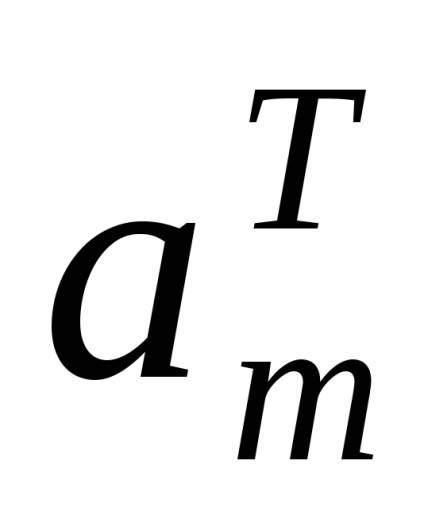
Feladat 2.13. Rate fáziseltérés sebességek osnovnyhTE0 iTM0 módok szimmetrikus sík hullámvezető a következő paraméterekkel :. N1 = 1,48; n2 = 1,475, V = 2. A hullámhossz a sugárzás, hogy ravnoy1,3 mikron.
Feladat 2.14. Rate különbség állandó rasprostraneniyaTE2 módok iTM2 szimmetrikusan sík hullámvezető a következő paraméterekkel :. N1 = 1,48; n2 = 1,47, V = 6. A hullámhossz a sugárzás, hogy ravnoy1,3 mikron.
Feladat 2.15. Becsült méret intermodális diszperzió egymódusú sík hullámvezető szimmetrikus paraméterekkel :. N1 = 1,48; n2 = 1,475, V = 1,5, nem tekinthető a skalár közelítés. hullámvezető hossza 1 m, az emissziós hullámhossz 1,3 mm.
Feladat 2.16. Alapján a peremfeltételek (2.3.3) és a rekurzió kapcsolatok hengeres funkciók (P3-P4) megkapja a karakterisztikus egyenlet (2.3.5) az optikai szál.
Feladat 2.17. A rekurzív sorozat hengeres funkciók (P3-P4) azt mutatják, hogy a bal oldalon a karakterisztikus egyenlet (2.3.5) lehet átalakítani, hogy
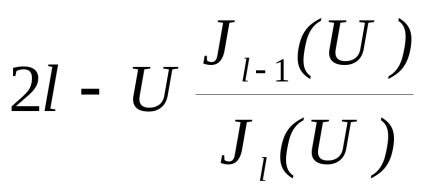
Feladat 2.18. A aszimptotikus kifejezéseket hengeres funkciók (P5) azt mutatják, hogy közel a cutoff (priUV, W 0) jobb oldalán egyenlet (2.3.5) hajlamos k2l.
Feladat 2.19. Mik a gyökerek lesz a karakterisztikus egyenlet (2.3.5), közel a cut-off divat LP0m, Prim = 1, 2, 3?
Feladat 2.20. Milyen módok is izgatott az optikai szálas Priv = 3, V = 5 és V = 8?
Feladat 2.21. Az emissziós hullámhossz 1,3 mikron vezetjük be az optikai szál. A törésmutatója a szál mag 1,47; héj - 1465. KakieLP divat, hogy irányítsák az optikai szál, ha a sugár a szál mag 5 mikron? 10 mikron?
Feladat 2.22. ModyLP11 cutoff fordul elő egy optikai szálon egy hullámhosszon 1,48 mikron. Mi lesz a mód szál szerkezetének hullámhosszon 1,3 mikron; 1,2 mikrométer és 0,8 mikrométer.
Feladat 2.23. A törésmutatója mag szálat egyenlő 1,47, a refrakciós index különbség a mag és a burkolat - 0,003. Hogyan válasszuk ki a mag méretét, hogy egy hullámhosszon 1,55 mikron, ezt a szálat egyetlen mód?
Feladat 2.25. Számoljuk ki a terjedési állandó modyLP11. gerjesztettük volny1,3 mikron hosszúságú az optikai szálban C paraméterek :. n1 = 1,48; n2 = 1.477, = 5,3 m.
Feladat 2.26. A bemeneti oldalon az optikai szál izgatott modyLP01 iLP11. Az elektromos mező oszlik modyLP01 bemeneti végén sík törvény alapján
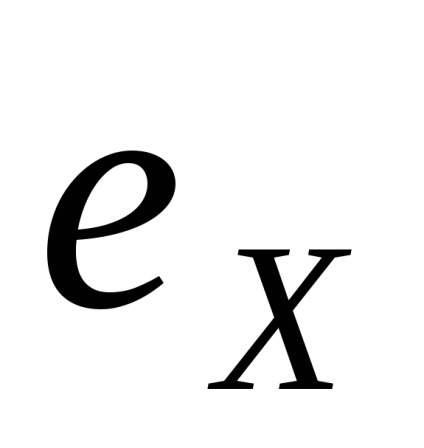

Feladat 2.27. Construct polarizációs tér eloszlása a még HE22 módot a keresztmetszeti síkban a szál.