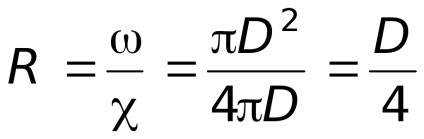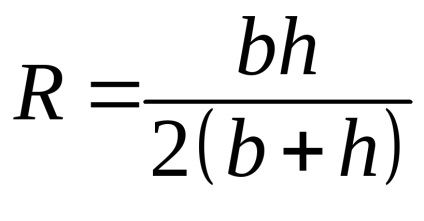Gyakorlati alkalmazása a Bernoulli-egyenlet

Ennek alapján Bernoulli-egyenlet épül számos eszközt, például egy vízóra Venturi sugárszivattyúhoz, kidobó, carbo-ra-a madárriasztó dugattyús motorok, és mások.

1. példa A vízmérő egy Venturi-tompa a rövid cső szűkülettel a közepén (ábra. 3.13). A legszélesebb része Lovina és hegyi-telepítve, vagy piezométerek, vagy differenciál nyomásmérő-CIÓ.

Alkalmazzuk a Bernoulli-egyenlet szakaszok 1-1 és 2-2 veszteség nélkül és

.

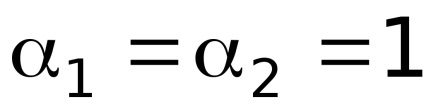
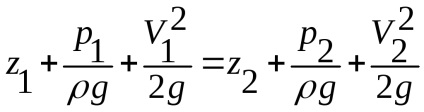
Transzformációs egyenlet az alábbiak szerint:

.

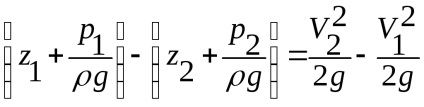
Szerint (ábra. 3.13) különbség a bal oldali része egyenlő h.

;

;

.

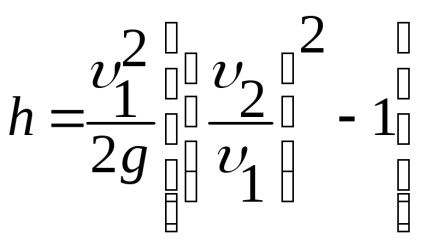
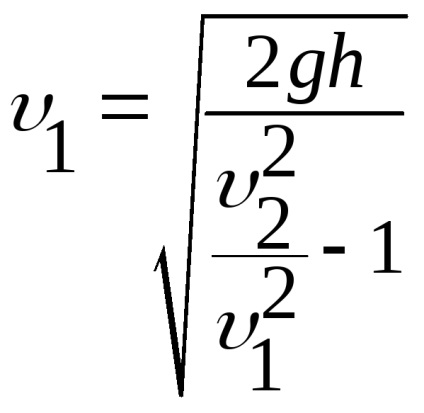
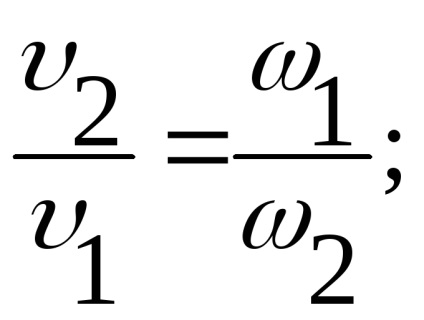
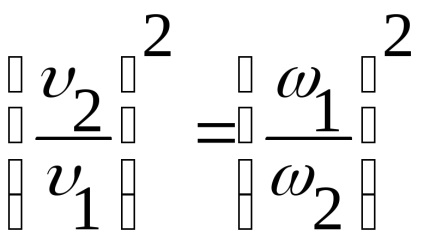
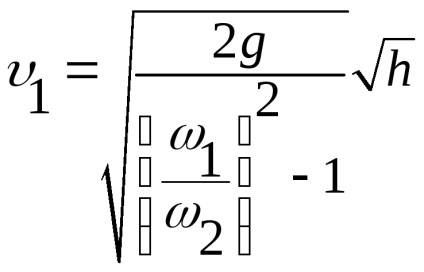
Használata áramlási egyenlet

, átalakítani képletet formájában

.

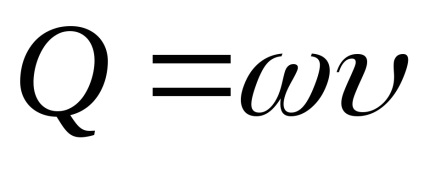
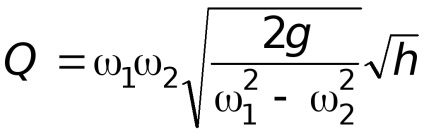
Jelöljük állandók keresztül

- a vízmérő állandó, akkor - elméleti lefedettség. Az akció-feno- vízmérő áramlási sebességet úgy határozzuk meg a képlet

,

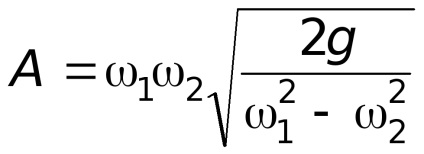
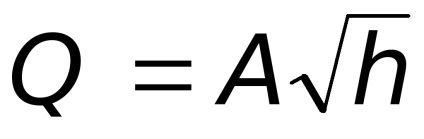
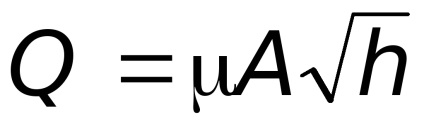
az áramlás együtthatója a vízmérő.

2. példa A porlasztó dugattyús belső égésű-Rania szolgál tüzelőanyagot szállító, és ezt összekeverjük a légáram (ábra. 3.14). Az áramlás a beszívott levegő a mozgás-tor szűkíti ahol a benzin van szerelve permetezőgép.

A levegő sebessége ebben a szakaszban megnő, a nyomás csökken szerinti Bernoulli-egyenlet.

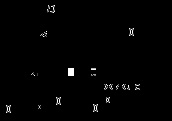
Most találtunk korrelációt a tömeg és a felhasznált benzin Gb vozduhaGv a megadott razmerahD és d együtthatók és pro-TIV-ment a légcsatorna (akár rész 2-2) és v zhiklerazh.

Írunk a Bernoulli-egyenlet a levegő áramlását (szakaszok 0-0 és 2-2), majd a benzin patak (szakaszok 1-1 és 2-2), és megszerezni a

i = 1.

;

.

.

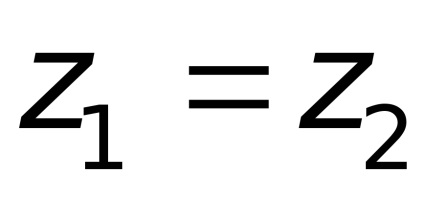
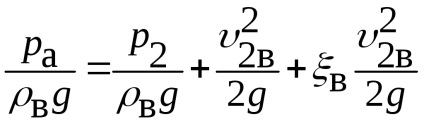
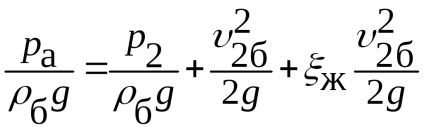
Mivel a súlya költségek

.

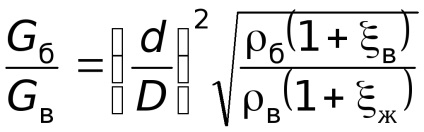
3. példa Pitot cső széles körben használják mérésére a sebessége a víz és gáz. Mi alkotják a Bernoulli-egyenlet szakaszok 1-1 és 2-2. Kuo-rizontalnaya összehasonlítása síkban 0-0 áthalad egy cső zokni (ábra. 3,15)

.

mert

; akkor volt, amely mögötti pici-Shem:

.

.

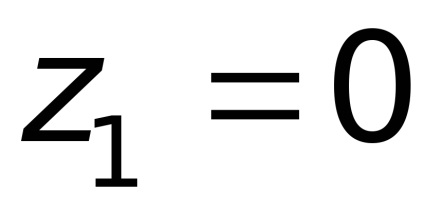
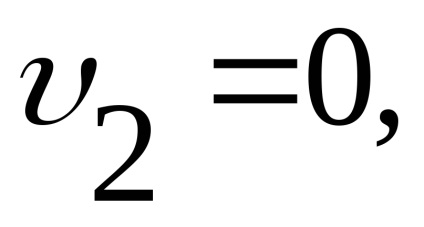
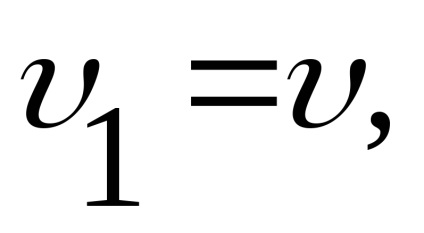
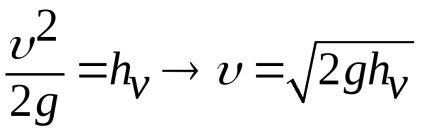
tesztkérdések

1. Írjuk be a Bernoulli-egyenlet az elemi folyamok egy súrlódásmentes folyadék, és bemutatják a beérkező bele.

2. Mi különbözteti meg a Bernoulli-egyenlet valós folyadék áramlását a Bernoulli-egyenlet az elemi stream?

3. Az úgynevezett teljes fajlagos energia áramlását?

4. Magyarázd fizikai értelmében a Coriolis tényező a Bernoulli-egyenlet.

5. Magyarázza értelmében az energia a Bernoulli-egyenlet.

6. Az úgynevezett piezometrikus és hidraulikus gradiens?

7. Példák A gyakorlati alkalmazásának Bernoulli-egyenlet Ber.

8. A modell alapján kapott levezetése a Bernoulli-egyenlet az áramlás a valós zhidkosti

9. Mi a piezometrikus nyomás és sebesség?

Az úgynevezett teljes nyomás?

3.12. Hidraulikus ellenállás. Módok folyadék mozgás

Amikor a tényleges folyadékok mozgását különböző hidraulikus rendszereket pontosabb becsléséhez a nyomásesést leküzdésében tűzcsapok-Do-cal ellenállását. Pontos számviteli Ezen veszteségek nagyrészt op re hasadó megbízhatóságát műszaki számítások. Ezen túlmenően, ez lehetővé teszi, hogy megtalálja a gazdaságilag célszerű megoldás, amely mintegy Lada-e kellő mértékben a tökéletesség. Erre a REQ di mo van egy világos megértése a mechanizmus mozgásának a folyadék.

A folyamat során a kutatás ismert fizikus Reynolds 1883-ban azt nem igazolta azt az elméletet, hogy két mozgási módokat zsidó eredetű. Ez elsősorban lamináris mozgás zsidó-csontok megfelelő, alacsony sebességgel. Lamináris mozgás lehet tekinteni, mint mozgását az egyes rétegek folyékony részecskék történik keverés nélkül.

Nagyobb sebességnél a folyadék mozgás figyelhető turbulens rendszer ( „turbulentus” Latin - az örvény). Ta-valami mozgalom kaotikus.

Hogy értékelje a működési mód folyékony Reynolds nélkül bevezetett dimenziós feltétel Re, amely figyelembe veszi a hatását sebesség

v. átmérője (a jellemző méretek) , plotnosti és di-na-mi cal vyazkosti:

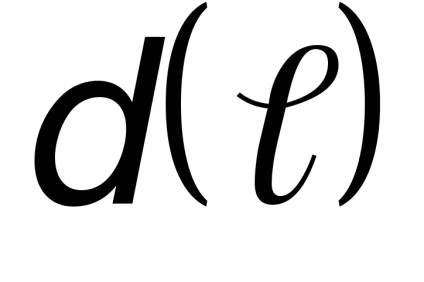
A határ a létezését egy olyan rendszer a zsidó-csont mozgás határozza meg két kritikus értékek Re: LO-it

és a felső.

Így, amikor

> Re csak lamináris, míg a