Diszkrét átalakulások és azok főbb tulajdonságait, 3. oldal
torzítás dualitás egy tétel egy műszak tétel. Ezekben tételek működés terén az eredeti képet és megfordult.
3. példa találunk rács képe f függvény [n] = e l n sh egy
A kép sh egy, megkapjuk alapján az elmozdulás a tétel:
3. tétel A kép különbségeket.
Az első különbség funkció latticework
Alapján elmélet lineáris és nyíró szerezni
D = (e q - 1) F * (q) - e q f [0] (3,15)
A második különbség funkció latticework
Δ 2 f [n] = Af [n + 1] - Af [n]
Alapján a váltás tétel és az egyenlet (3.15), az átalakítás után kapjuk
D = (e q - 1) 2 F * (q) - e q (e q -1) f [0] - e q Af [0] (3,16)
A k-adik különbség a rács funkció a következő kifejezés:
D<Δ k f[n]> = (E q - 1) K F * (q) + e q Σ (e q - 1) k -1- r Δ r f [0] (3.17) r = 1
Ott kell tekinteni Δ 0 F [0] = f [0].
4. példa Nézzük először különbség image rácsos exponenciális függvény f [n] = E a n. A képlet szerint (3,15), kapjuk:
e q - E egy e q - e egy
4. Tétel A kép összegek
Tekintsük az, hogy meghatározza az rács funkciók:
A kép a különbség egy f függvény [n] összhangban az előző tétel:
mint az összegérték n = 0 értéke nulla. Következésképpen, [m] összegének rács képe f függvény, mint
5. példa találjuk az eredeti képnek megfelelő
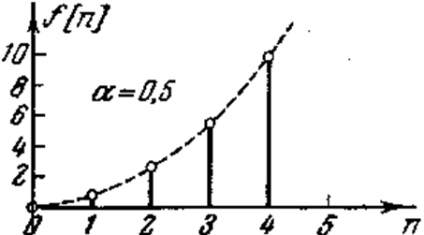
Ábra. 3.4. A rács funkció az 5. példában.
Alkalmazási példák tételkör kép különbség az összegeket és azt mutatja, hogy a faktor (f q - 1) a diszkrét Laplace-transzformáció szerepet játszik paraméter preobrazovaniyaqilisv szokásos Laplace-transzformáció és a kommunikáció létrehozására hivatalos szereplő módszer elméletben differenciaegyenletek diszkrét Laplace-transzformáció.
Ezek a tulajdonságok, valamint a sebességváltó-tétel alapjául szolgáló megoldási módja lineáris differenciálegyenletek.
5. Tétel szorzás képek (alvadási tétel az igazi domain).
Ez a tétel az egyik legfontosabb tételek alkalmazásokhoz. Ez lehetőséget ad arra, hogy megtalálják az eredeti képet a termékről, ha az eredetit ismert tényezők.
Elvégzése a szorzás a sorok a jobb oldali a Re q> sc. ahol sc - a legnagyobb a vízszintes konvergencia, megkapjuk:
mivel az N Meghatározás szerint a D-konverzió kapjunk Ezek a képletek nevezzük összeomlása az igazi domain. Tétel 6. Az ellenszolgáltatás rács funkciók (ellenszolgáltatás tétel). A tétel teremt kapcsolatot a képet és egy véges érték a rács funkciókat. A undisplaced rács funkció kielégíti az alábbi összefüggést: lim f [n] = lim (e q - 1) F * (q). (3,20) hasonlóképpen a kificamodott léc funkciók: lim f [n, e] = lim (e q - 1) F * (q, e). (3,21) Tétel 7. A kezdeti értéke a rács funkciók (kezdeti érték tétel). A undisplaced rács funkció kielégíti az alábbi összefüggést: f [0] = lim f [n] = lim (1 - e -Q) F * (q) = lim F * (q), (3,22) hasonló reláció kificamodott léc funkciók:Kapcsolódó cikkek