A spektrális ábrázolását periodikus jelek
1. harmonikus rezgés.
Matematikai modell a harmonikus oszcilláció:
u (t) = Ums sin (# 969; st + # 966; s) (11)
Mint látható a matematikai modell, a spektrum a ingadozások be egy harmonikus összetevőt, amely frekvencián # 969; s. A magasság a komponens a spektrum amplitúdója megegyezik az amplitúdó-ingadozások Ums, és egy fázistranszfer-spektrum - a kezdeti lengések # 966; s. Ezen túlmenően, az építőiparban a spektrum szükséges közötti időben jelet, és a spektrum diagram amplitúdók. Az amplitúdó a spektrum komponenst kell egyeznie rezgési amplitúdó korrekciót az időzítési diagramot.
Meg kell jegyezni, hogy gyakoriságának növelése a jel komponens eltávolítjuk azt a frekvencia tengelyen a nulla (13. ábra).
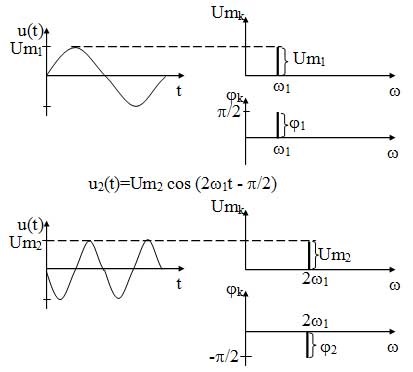
13. ábra - A spektrális ábrázolását harmonikus rezgések
Amint az az ábrákon látható, a spektrum a harmonikus rezgések diszkrét és korlátozott.
2. Az időszakos, nem-harmonikus jelek.
A fő jellemzője a spektrális ábrázolását a jel jelenléte a spektrális komponensek sokaságának a spektrum. Ezek a jelek leírható egy Fourier-sor, amely szerint:
t. e. a jel lehet összege által képviselt az állandó komponens és több harmonikus összetevők.
Átalakítás a sorozat segítségével trigonometrikus tulajdonság
sin (x + y) = sin x cos y + cos x sin y (13)
Feltételezve, hogy x = # 966; K és Y = k # 969; ct kapjuk:
Mivel ÚMK és # 966; k a paramétereket a sorozat, akkor kijelöli együtthatók
UMK sin # 966; k = ak; UMK cos # 966; k = bk (15)
Ezután a sorozat lesz:
számos paraméter lehet definiálni együtthatók ak és bk:
Az amplitúdó a DC komponensen és együtthatókat lehet meghatározni a jel értéke u (t):

Egy sor, hogy, ha a jel által leírt egy még f (t) = f (-t), akkor a sorozat csak cosinus komponensek bk = 0, ha páratlan függvény (f (t) ≠ f (-t) ), az örömmel amely csak szinuszos összetevők (ak = 0).
Tekintsük a spektrális ábrázolását az időszakos, nem-harmonikus jeleket egy példa egy periodikus szekvencia négyszögletes impulzusok (PIP).
A következő paramétereket kell kiszámítani, amikor az építőiparban a spektrum:
a) terhelhetőség jel:
b) a konstans értékét komponens:
c) a frekvencia az első harmonikus a spektrum, amely egyenlő a jel frekvencia:
g) az amplitúdó spektrumát harmonikus összetevők:
Az építőiparban a spektrum szükséges megjegyezni a következő funkciókat:
1. Minden harmonikus komponensek frekvencián, amelyek többszörösei az alapfrekvencia (969 # 2; 1, 3 # 969; 1, 4 # 969; 1, stb ...);
2. A spektrum tartományok:
a) van egy spektrum; STD szirmú jellegű, azaz a spektrum kiosztani sokaságát „szirmok” ..;
b) a számát harmonikus komponenseit a szirmok függ a terhelhetőség és egyenlő q - 1;
c) az amplitúdó a harmonikus összetevők, amelyek a frekvenciák, amelyek többszörösei a munkaciklust, nullával egyenlő;
g) alakja a spektrum boríték jelöljük - szaggatott vonal simán csúcsokat összekötő harmonikus komponensek;
d) az a pont, ahonnan jön a boríték vagy egyenlő 2U0 2I0.
3. a fázis a spektrum:
a) minden harmonikus összetevők frekvencián, amelyek nem többszöröse a működési ciklust, azonos magasságú egyenlő n / 2 (90 °);
b) minden harmonikus összetevő egyetlen lebeny ugyanaz az előjele, és a szomszédos ellenkezője.
c) komponensek frekvencián többszörösei a munkaciklus van egy kezdeti fázis nullával egyenlő.
Pip-spektrumokat, ha a kitöltési tényező q = 3 a 14. ábrán látható.
Mint látható a diagramok; STD spektrum diszkrét és korlátlan. Ezért, a spektrum szélessége fogadására frekvenciatartomány, amelyen belül az első két lebeny, hiszen a bennük tartalmazott mintegy 95% a jel energia ..:
# 916; fs = 2 / # 964; u. (26)
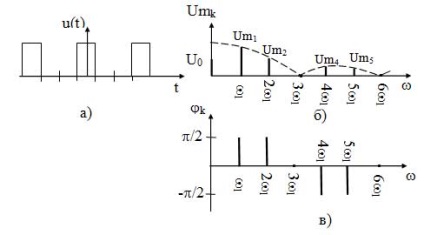
14. ábra - A spektrális képviselete; STD: a) egy idődiagram; b) spektrális diagram az amplitúdók; c) egy spektrum diagram fázisok
Amint látható, a spektrális szélessége körlet interfész pontokat csak attól függ, az impulzus időtartam és független annak időszakban.
3. Nem periodikus jelek.
Mivel a nem-periodikus jelek nem választhatja időszakban t. K. T → ∞, majd kiszámítja és ábrázoljuk a spektrum azonos eljárás alkalmazásával, hogy lehetetlen a periodikus jelek. Azonban, a tudás a spektrum ezen jelek szükséges, azaz a. K. összes információ jelek nem periodikus. A konstrukció egy periodikus jel spektrumának előállított következő eljárással: szignál mentálisan szakaszos egy tetszőleges időszak, amely építeni ddlya spektrum. Ezután, a szabályozó folyamat a végtelenbe hagyta időszak (T → ∞) (15. ábra). A frekvencia az első harmonikus, és ennek megfelelően, a távolság a felharmonikus komponensek általában nulla (f1 = 1 / T), úgy, hogy az összes komponens összeolvad egymással és egy olyan folytonos spektrum.
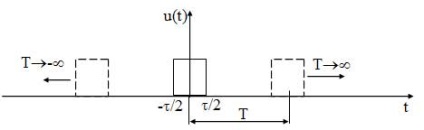
15. ábra - az impulzusjel u (t) és reprezentációja periodikus jel
Az alakja a spektrum boríték jelöljük nem periodikus jelek (folytonos vonal) (16. ábra).
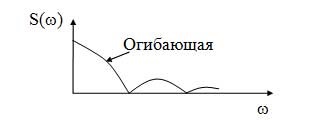
16. ábra - A spektrális chart nem periodikus jel
A Fourier-sor ilyen jelek, továbbá nem lehet rögzíteni, t. K. Ebben az esetben, az amplitúdó a DC komponensen és az együtthatók ak és bk nulla. Ebben az esetben a jel értéke bármikor is nulla, ami nem igaz. Ezért az ilyen használata a jelek Fourier-transzformáltja:
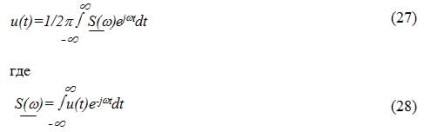
Expression (27) az inverz transzformációt, és (28) közvetlen Fourier-transzformáció.
A mennyiség S (# 969;) van az integrált spektrális sűrűség u (t) jel nem periodikus. Ez egyenlő:
ahol S (# 969;), a spektrális sűrűség az amplitúdók vagy amplitúdóspektrumot periodikus jelet, és a # 966, (# 969) - nem periodikus fázisú spektrumú jel.
A spektrális sűrűsége amplitúdóinak aperiodikus jel bármely frekvencián # 969; egyenlő a teljes amplitúdó található egy kis csík # 916; # 969; a közelben a frekvencia # 969; újratervezi 1 Hz.
Időzítés diagramok és spektrális amplitúdója sűrűséget téglalap és háromszög impulzusokat a 18. ábrán látható:
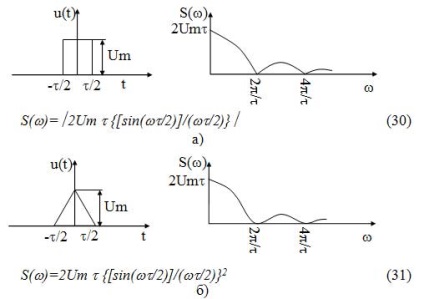
18. ábra - A spektrális ábrázolását nem periodikus jelek: a) egy négyszögletes impulzus; b) egy háromszög alakú impulzus