A lineáris konvolúciót véges szekvenciák

2.24. A lineáris konvolúciót véges szekvenciák

.. Vegyünk két véges szekvenciák hossza és az számít, tehát eltér a nullától, a - a. Lineáris vagy aperiodikus konvolúciót ezen szekvenciák olyan szekvencia viszonya határozza meg

ahol a nulla megfelelő időközönként. Ábra. 2.30 példa a szekvenciák és a. Nyilvánvaló, hogy a szekvencia véges, és a hossza a minták.

Fent azt mutatja, hogy megszorozzuk a DFT két véges szekvenciák és megtalálása az inverz DFT termék, megkapjuk ugyanazt az eredményt, mint a kör alakú konvolúciós egyenértékű periodikus származó szekvenciák véges adatsorozatok. Alapján e (lásd. Még a példát ábra. 2,29), lehet beszerezni viszonylag egyszerűen lineáris konvolúciót két véges szekvenciákat. Konvolúciós periodikus szekvencia periodikus és ugyanabban az időszakban, mint a szekvenciák magukat. Mivel konvolúciós időszakban (ábra. 2.30) egyenlő számít, így egy ilyen időszak a kör alakú konvolúciós az szükséges, hogy tartalmazott mintákat az adott elért kiegészítik egymást a két szekvencia megfelelő számú nulla minták. Miután ez megvan -pont DFT kibővített szekvenciák többszörösen és végre inverz DFT termék.

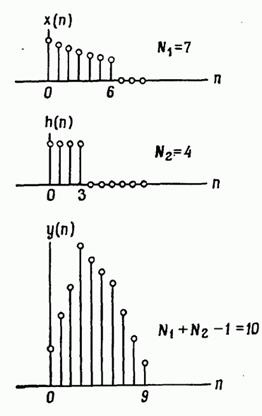
Ábra. 2.30. Lineáris (aperiodikus) konvolúciós.

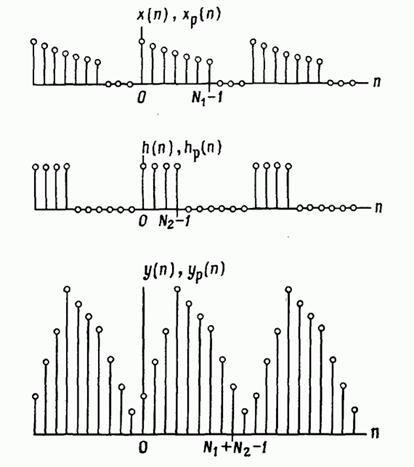
Ábra. 2.31. Számítása lineáris konvolúció kör alakú konvolúciós eszközökkel.

Az eredmény a kívánt összehúzódás. Ábra. 2,31 szemléltető ezeket a műveleteket mutatjuk egyenértékű periodikus szekvenciákat használjuk a számítás a cirkuláris konvolúció. Nyilvánvaló, hogy a kívül a szülői szekvenciák véges hosszúságú, és zéró-értékekhez hozza időszakban a kívánt értékre, és elkerüli körkörös szuperpozíció jellemző cirkuláris konvolúció. Ennek eredményeképpen, minden időszakban a szekvencia (ábra. 2,31) egybeesik (ábra. 2.30). A fenti módszer számítási konvolúció két véges szekvenciák DFT úgynevezett gyors konvolúciót algoritmus közvetlen ellentétben a számítási módszerét az összeget (2.165), vagy lassú úgynevezett közvetlen konvolúció. A „gyors” azért használjuk, mert a DFT lehet számítani, gyorsan és hatékonyan használja az egyik algoritmusok Fast Fourier Transform (FFT). Belátható, hogy még mérsékelt értékekkel (például körülbelül 30) gyors konvolúciós gyakorlatilag egy egyenes vonal. Ezért a módszert tartják fontos számítási eszköz jelfeldolgozás.

A gyakorlati alkalmazás fontos megjegyezni, hogy a fenti példában a DFT méret nem feltétlenül határértéknek. DFT elvégezhető tetszőleges számú minta kielégíti a feltételt. Ha ez a feltétel teljesül, ellentétben a fent leírt módszerek szekvencia és kiegészítik egymást száma nulla minták. Ennek eredményeként egyenértékű lesz periodikus szekvenciája nullák végén időszakokban. Nyilvánvaló, hogy ezek a különbségek nem torzítja el a kívánt eredményt. Ability önkényes választás azért lényeges, mert a gyakorlati algoritmus számítási DFT eltérő hatékonysággal egyenlőtlen. Például néhány szükséges algoritmusok, hogy megegyezzen egy ereje 2. Ebben az esetben, ahogy van, hogy válasszon egy számot egyenlő 2 fok, és nem kevesebb, mint.