Ohm törvénye a láncrésznek
A lecke típusa. Új anyag tanítása.
Oktatás: az áramerősség, az áramkör homogén szakaszának feszültsége és a szakasz ellenállása közötti kapcsolat megteremtése.
- fejleszti a kísérletek eredményeinek megfigyelését, összehasonlítását, összehasonlítását és általánosságát;
- folytassák a képzettség megteremtését a fizikai tudomány elméleti és kísérleti módszereinek használatára, hogy igazolják a témával kapcsolatos következtetéseket és megoldják a problémákat.
Oktatási: a kognitív érdeklődést a tantárgyban, a képletek memorizálására szolgáló racionális módszert oktatva.
- Tegyük fel, hogy az áram egyenesen arányos a vezeték végén lévő feszültséggel, ha a vezető ellenállása nem változik;
- Tegyük fel, hogy a lánc szegmensben lévő erő fordítottan arányos az ellenállással, ha a feszültség állandó marad;
- Ismerje Ohm törvényét a láncrészre;
- Képes meghatározni az áramot; a feszültség a grafikonon az ilyen mennyiségek közötti kapcsolat és a mentén - a vezető ellenállása;
- Képes legyen megfigyelni, összehasonlítani, összehasonlítani és általánosítani a demonstrációs kísérlet eredményeit;
- Ahhoz, hogy a probléma megoldásakor alkalmazható legyen az Ohm-törvény egy láncrészre;
- A dimenzió ellenőrzésének készségeinek gyakorlása;
- A kapott eredményeknek a mennyiségek valós értékével való korrelációjának képességeit gyakorolni.
Demo áram- és feszültségmérő műszer, az aktuális forrás B-24, a legfontosabb összekötő kábel, minta ellenállás bolt, TCO, képernyő, mágneses tábla, mágnesek, portré Ohm, asztalok képleteket.
1. Szervezeti momentum.
Tanár: Helló, üljön le (szolgálatban, távol).
2. A tudás aktualizálása.A tudás elsajátításának tesztelése érdekében a didaktikai játék "Tesztelje meg magad!". A játék két részből áll. A munka első részében a gyerekek kiválasztják az elnevezést, a képletet, a mértékegységeket, a mérőeszköz egyik fő jellemzőjének mérését. A második részben a tanulók töltsék ki a táblázatban szereplő hiányosságokat. Az osztály három lehetőségre oszlik. Minden lehetőség adott feladatot kapott. A munkák értékelése kölcsönös hitelesítéssel történik.
3. Motivációs szakasz.A korábbi tanulmányok során három olyan mennyiséget tekintettünk, amelyekkel bármely elektromos áramkörben foglalkozunk - ez ... (áramerősség, feszültség és ellenállás). De az életben és a gyakorlatban nem elég külön-külön megismerni a villamos áramköröket jellemző fizikai mennyiségeket, ezeket egymástól függően kell figyelembe venni. Megmutatjuk a mai interdependenciát a leckében.
Írja le leckünk témáját: "Ohm törvény a lánc helyén".
A jelentősége kutatás Georg Ohm pontosan azt mondta, a fizika professzora a University of Munich Eugen Lommel Cornelius Joseph megnyitóján emlékmű a tudós 1895-ben „A felfedezés Ohm sütött egy fáklyát, megvilágítva a terület villamos energia, amely neki volt sötétnek. Om az egyetlen helyes utat mutatta az érthetetlen tények áthatolhatatlan erdején. Figyelemre méltó fejlődéséről elektrotechnika, amelyhez nézte csodálkozva az elmúlt évtizedben, csak úgy érhető alapján a felfedezés Ohm. Csak ő képes uralni és irányítani a természeti erőket, akik képesek lesznek feloldani a természet törvényeit. Om a természetből rejtélyt rejtegetett, és átadta a kortársaknak. "
Kérdés: Milyen rejtélyt régóta Om rontott a természettől, és adta kortársainak? Ismerd meg.
4. Az új anyag tanulásának szakasza.A mai leckében meg kell oldanunk a következő problémát: meg kell tudnunk állapítani, hogy az áramkör szakaszán az áram erőssége függ az alkalmazott feszültségtől és az ellenállás nagyságától egyidejűleg. Ez a lecke fő célja.
Tehát a mai leckében végzett munkát szakaszokban végzik.
1) Először meghatároztuk a jelenlegi erő függőségét a feszültségre, ezt a függést matematikailag írjuk le és kísérletileg ellenőrzik.
2) Az áram erősségének és az ellenállásnak az állandó feszültséggel való kapcsolatának megállapítása; írja le az eredményeket egy táblázatban, következtetést vonhatunk le e függőség jellegéről.
3) Legyen általános következtetés arról, hogy az áram egyidejűleg függ-e a feszültségtől és az ellenállástól, azaz. akkor megoldjuk a lecke fő feladatát.
1. Határozzuk meg az áramerősség függését a kísérlet feszültségén.
a) A demo tábla tartalmaz egy áramkört: áramforrást, reosztátot, ampermérőt, ellenállást, voltmérőt, kulcsot.
b) Vezessen egy áramkört a táblán.
c) Kapcsolja be az áramkört. A voltmérő 2V-ot mutat. Mi az ampermérő? Erőssége 0.4A.
Növelem a feszültséget -3V-ra. Megváltozott az ampermérő értéke? Igen, az áramerősség áramerőssége 0,6A.
Növelje a feszültséget - 4V-ra. Hogyan módosult az áramerősség? Az áramkör áramát 0,8A-val növeltük.
Az eredményeket az asztalra írjuk és rajzolunk egy grafikont:
Megváltozott-e a vezető ellenállása? Nem, állandó: R = hátrány.
Következtetés 1. R = const, I
2. Állítsuk össze a jelenlegi erőt és az ellenállást.
b) Lássuk tehát ezt a tapasztalatot. Az asztalon egy áramkört szereltek fel: egy áramforrást, egy ellenállástárolót, egy ampermérőt, egy voltmérőt, egy kulcsot.
b) Vezessen egy áramkört a táblán.
c) Állítsuk össze az I és R közötti kapcsolatot, U = const-val. A táblázatot felhívjuk a notebookba, és kitöltjük a kísérlet során.
Most a teljes ellenállás 4 ohm, a feszültség 5V. Mi az a áram az áramkörben? I = 1 A
Csökkenti az ellenállást a 2 ohm megváltoztatása nélkül a feszültség, áram az áramkörben most? I = 2 A. Most ravno1 ohm impedancia, feszültség még mindig nem változott menyaem.Kak áramerősség? I = 4
Tehát, nézzük az asztalt, mi a helyzet a jelenlegi erő és az ellenállás között? Rajzolj egy diagramot.
2. Következtetés: U = const I 1 / R esetén
3. Végezzünk egy általános következtetést arra vonatkozóan, hogy az aktuális függvény egyidejűleg függ-e az U-tól és az R.-ből.
Már két függõséget ismerünk. És most összekapcsoljuk ezeket a függőségeket egy képletbe. Magával hozhatjuk az elektromos áram egyik alapszabályát, amelyet Ohm törvénynek nevezünk:
Az áramkör szakaszában lévő áram közvetlenül arányos a szakasz végén lévő feszültséggel, és fordítottan arányos a szakasz ellenállásával.
"Om a természetből rejtélyt rejtegetett el, és átadta a kortársaknak" 1827-ben. 38 éves volt.
E törvény alkalmazásával kiszámíthatjuk a jelenlegi erősséget, tudva a feszültséget és az ellenállást, azaz a két mennyiség ismeretében, mindig megtalálhatjuk a harmadik.
5. Az új tudás alkalmazása
Szóval, srácok, milyen értékek függenek az Ohm törvényétől?
- az áramerősség, a feszültség és az ellenállás között.
Hogyan függ az áram a feszültségtől?
Hogyan függ az áram az ellenállástól?
Hogyan alakul az Ohm törvénye?
Oldjuk meg a problémát:
- függőségi görbék;
- kombinált feladat.
6. A tudás kezdeti ellenőrzése
Az elsődleges tudás asszimilációjának ellenőrzéséhez két feladatot alkalmaznak. Az osztály két lehetőségre osztható. A feladat körülményei a táblán jelennek meg. Az ellenőrzést kölcsönös hitelesítéssel végzik.
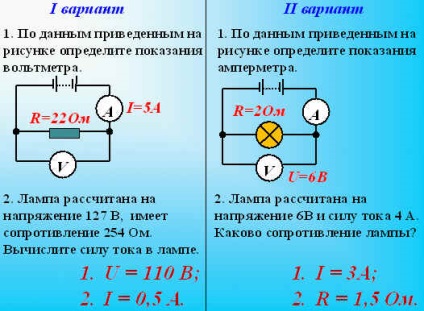
7. Házi feladat:
§§ 43, 44. Olvassa el;
2. Gyakorlat. 20 (1, 2, 3) p.88; Ex. 21 (2, 4, 6, 7) 91. oldal.
3. Történelmi referenciák készítése azokról a tudósokról, akiknek neve nagyon szoros kapcsolatban áll az Ohm törvényével.