Meghatározása erők az elemek egy monolitikus váz
Város Novopolotsk IIB területén súlya hótakaró.
Mivel a tervezett épület használatra szánt területén a Belarusz Köztársaság (nyissz 2.01.07-85, figyelembe véve változásokat №1), a teljes normál érték hó terhelés a vízszintes vetülete a fedél által meghatározott képlet:
, ahol SO = 1,2 - normatív tömeg értéke 1m2 hótakaró vízszintes talajon, μ = 0,66, tk. α<27, µ - коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие, α-угол покрытия, град.
Becsült értéke a hó terhelés szorzatából a normál érték 1,6:
Lineárisan rasperdelennaya ható terhelés a csavar fogja Loft elosztott terhelés egyenlő félszer a szélessége a tető egyenlő l = 2800 mm.
3.3 táblázat terhelések tetőtérben csapok 1m
Aránya terhelés megbízhatóság
hó (az épület)
3.5 táblázat terhelések 1m2 tetőtér
Aránya terhelés megbízhatóság
d = 0,02, r = 18,0 kN / m 3
d = 0,16 M, R = 3,0 kN / m 3
Vapor d = 0,002m, R = 9,1kN / m 3
RC lemez d = 0,22m, R = 25,0 kN / m 3
Lineárisan rasperdelennaya ható terhelés a csavar fogja Loft elosztott terhelés felével egyenlő a lemez szorozva a hossza átfedés egyenlő l = 4900 mm.
3.6 táblázat terhelések az 1. tetőtérben csavart a tetőtérben
Aránya terhelés megbízhatóság
Táblázat 3.7 terhelések tipikus emeleten 1m2
Aránya terhelés megbízhatóság
mozaik beton, δ = 0,025, r = 22,0 kN / m 3
esztrich M150 δ = 0,02 M. r = 18kN / m 3
duzzasztott agyag δ = 0,055m, r = 5,0 kN / m 3
tömeg lemezek δ = 0,22m, R = 25,0 kN / m 3
A számítás a terhelés az egyedüli az oszlop kell tekinteni a saját súlyát.
Statikus kiszámítása épület váz és meghatározása számított erőfeszítések történtek Raduga programot.
3.1.2 Statikus kiszámítása a keret.
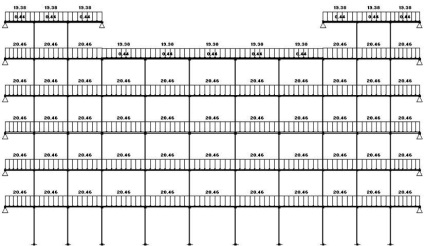
Ábra. 3.2 Becsült rendszer monolit keret épület (állandó terhelés).
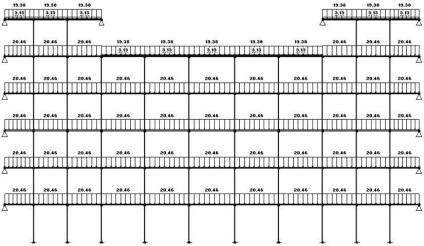
Ábra. 3.3 a számított diagram monolitikus építési vázat (állandó + élő terhelés).

Ábra. 3.4 számozása csomópontok és rudak
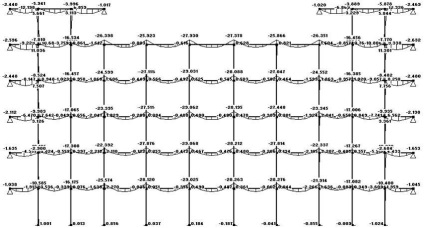
Ábra. 3.5 ábra hajlítási pillanatok (állandó terhelés)
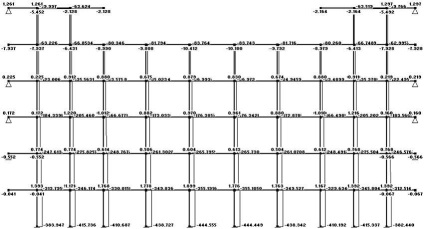
Ábra. 3.6 A diagram a hosszirányú erők (állandó terhelés)
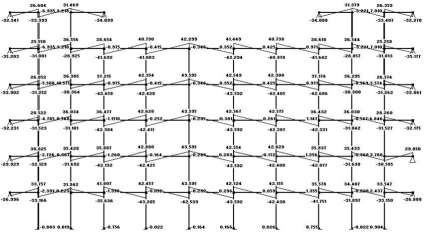
Ábra. 3.7 Plot nyíróerők (állandó terhelés)
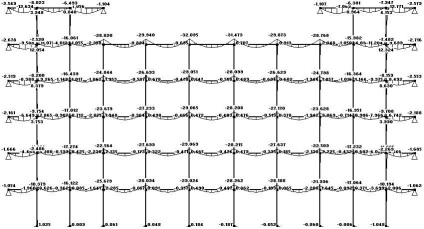

Ábra. 3.8 ábra hajlítónyomatékok (+ idő állandó terhelés)
Ábra. 3.9 ábra hosszirányú erők (állandó + élő terhelés)
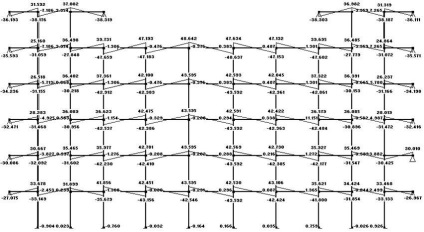
Ábra. 3.10 diagramja oldalirányú erők (állandó + élő terhelés)
Rajzok a belső erőket lehet mondani, hogy a legkedvezőtlenebb kombinációt terhelés állandó + hó, így a számított belső erők táblázatos formában csak akkor kap ez a kombináció a terhelés.
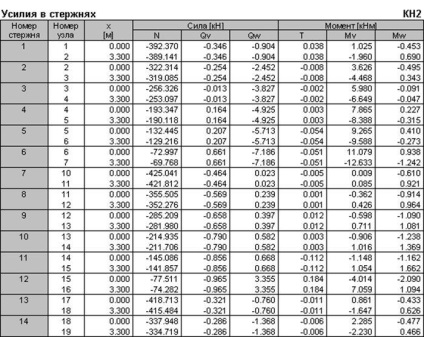
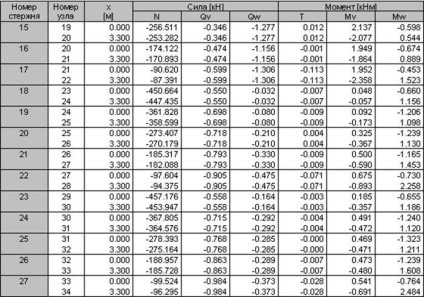
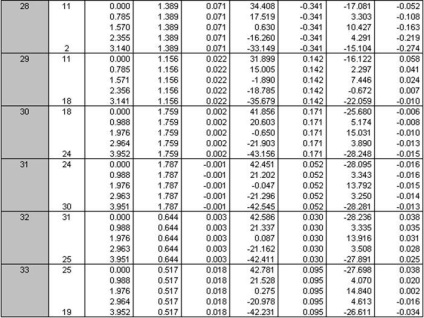
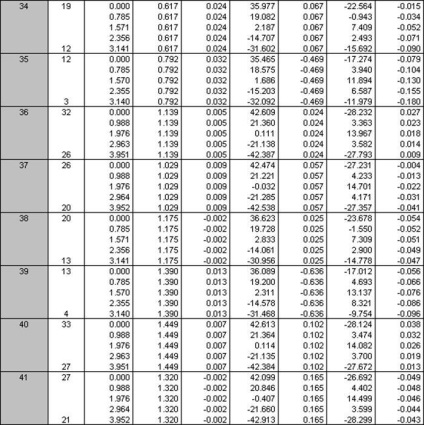
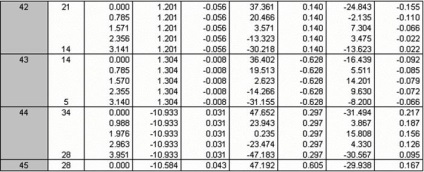
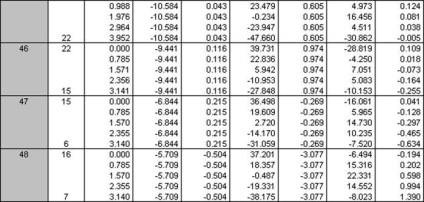
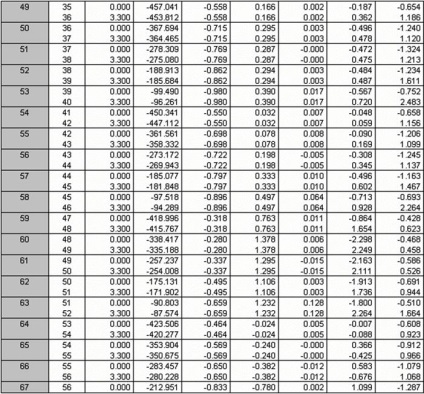
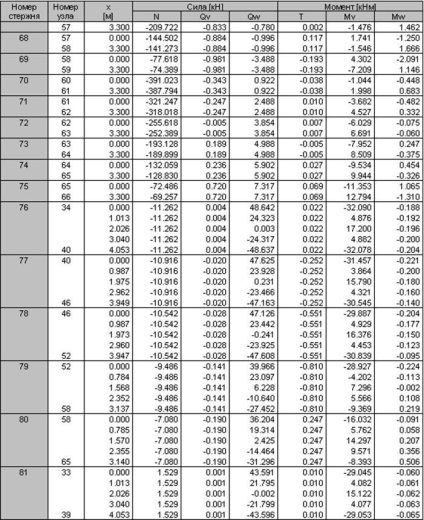
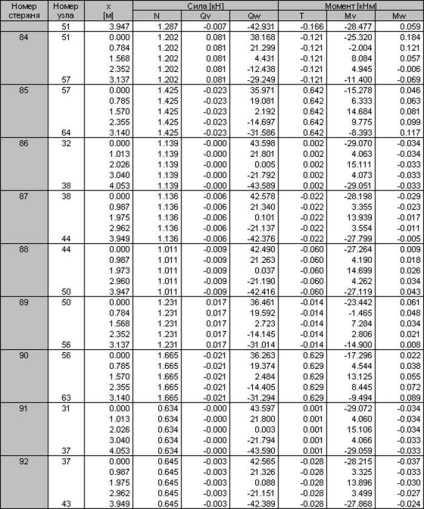
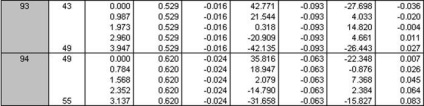
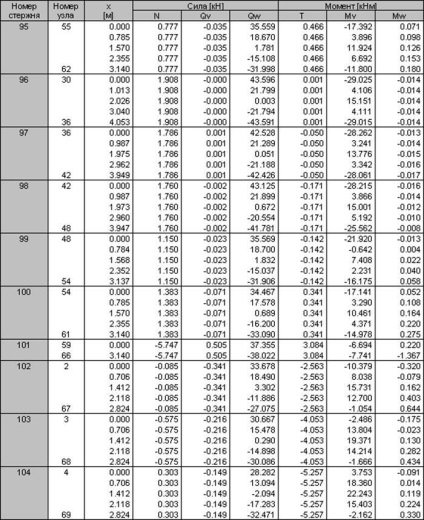
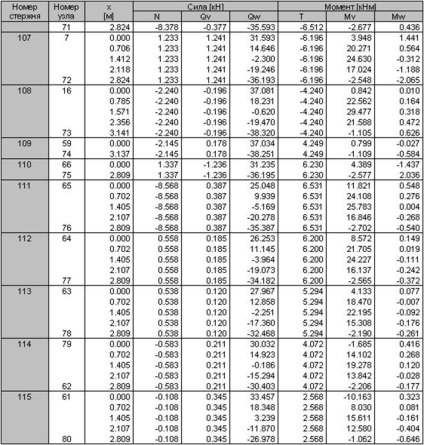
3.2 kiszámítása monolit oszlopok keret
A következő eredményeket kaptuk (az pincéjében az oszlop):
- gravitációs terhelés az oszlop:
- kombinálva nagruzkok maximális hosszirányú erő
Nmah = 457,04 + 509,88 = 52,8 kN, és a megfelelő hajlító nyomaték M = 0,187 kNm.
- állandó (hosszú) terhelések Nl = 417,12 + 52,8 = 469,92 kN, és a megfelelő hajlítónyomaték Ml = 0182 kNm.
3.2.1 Jellemzői beton szilárdságának és megerősítése.
Határozza meg a / 17 / és az alkalmazás konkrét szilárdsági jellemzők tekintetében az előre meghatározott környezeti páratartalom a művelet osztály HS3.
Beton nehéz, nem keményített, osztály C25 / 30:
Armatúra periodikus profil osztály S400, a standard ellenállás fyd = 400 MPa. A számított ellenállás fyd = 365 MPa. Szerint tabl.6.5 / 16 /.
3.2.2 kiválasztása keresztmetszetű szimmetrikus megerősítése.
Munka profilmagasság d = h - c = 40-4 = 36 cm, szélessége b = 40cm.
Excentricitásának erő: EO = M / N = 18,7 / 509,88 = 0,04sm.
Véletlen excentricitása: EO = h / 30 = 40/30 = 1,34sm vagy EO = lcol / 600 = 330/600 = 0,55 cm, de nem kevesebb, mint 1 cm.
Mivel az excentricitás erő EO = 0,04 cm-rel kisebb a véletlen excentricitása EO = 1,34 cm, fogadja kiszámításához a statikailag határozatlan rendszer EO = 1,34 cm.
Találunk érték pont a keresztmetszet tekintetében egy átmenő tengely súlypontja szakítószilárdságú tekintettel a véletlen excentricitás