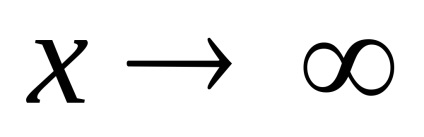
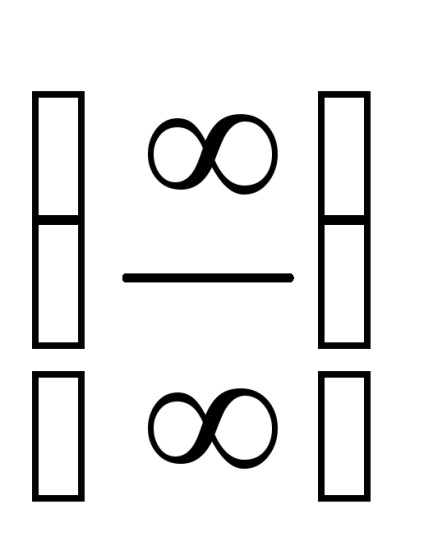
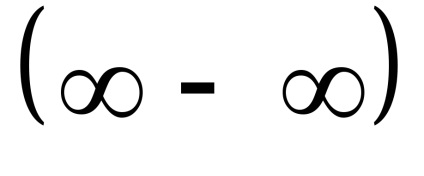
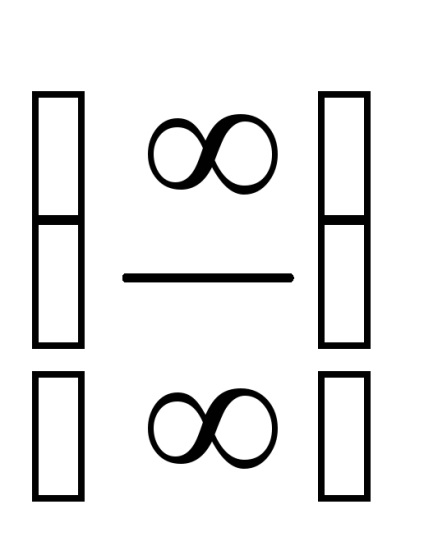
A határértékek a racionális függvények másodfokú kifejezéseket

Abban az esetben, bizonytalanság

kell bővíteni a másodfokú egyenletet tényezők. Ehhez

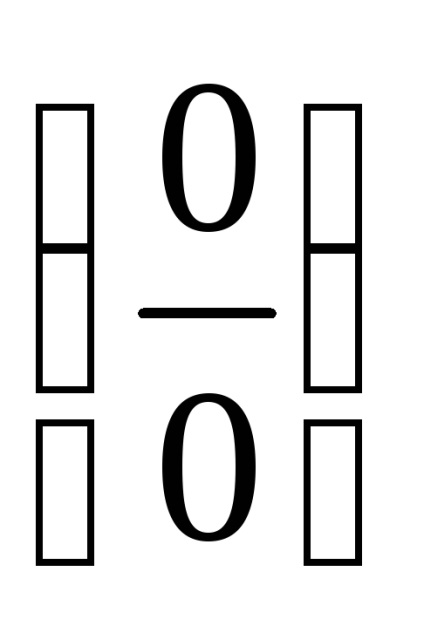
a) használni a személyazonosságát, ahol

és- gyökerek következő képlettel;

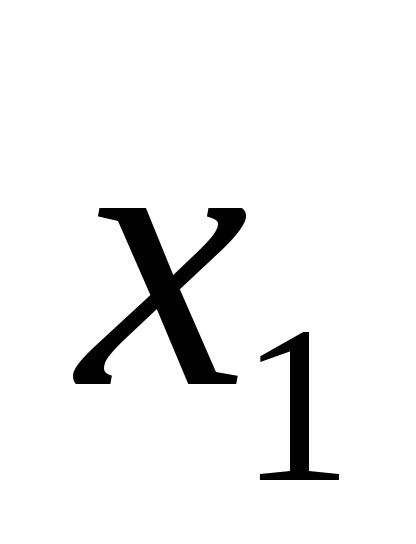
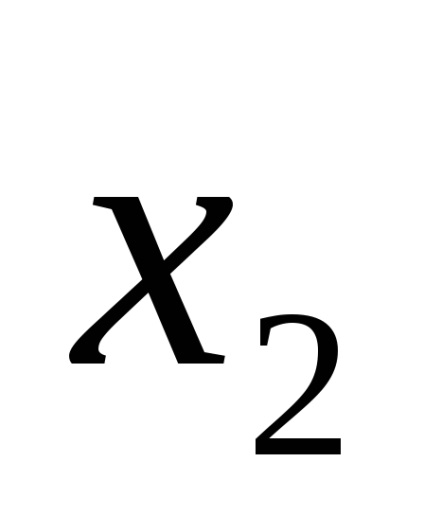
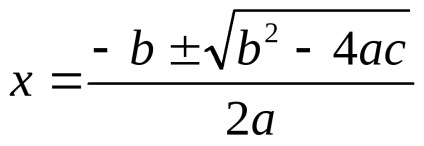
b) figyelembe veszi, hogy amennyiben a

- az egyik a gyökerek, és a többi gyökérMegtalálható az Térség tétel, például az egyenletből, ahol;

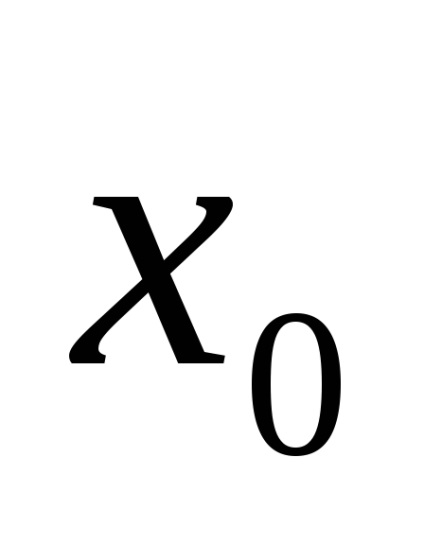
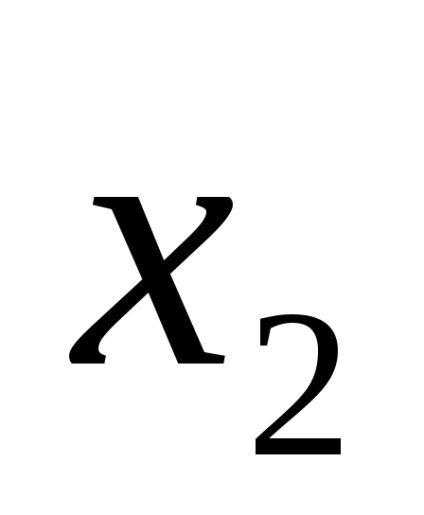
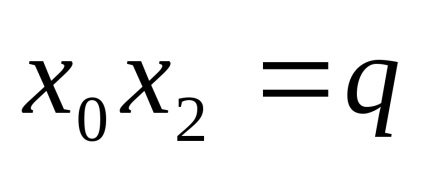
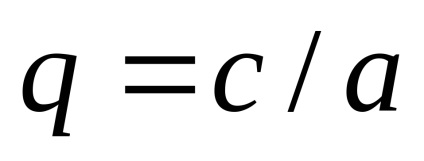
c) alkalmazni az egyenletet, ahol

.

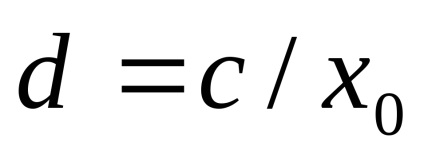
(Ii megoldotta a felhasznált egyenletek 1. út).

.

Az egyenletben szabad faktor osztva faktorral -10 Szembeszállás

(Number 4). Eredmény osztva egy ismert gyökér 2. nyert 2. gyökér.

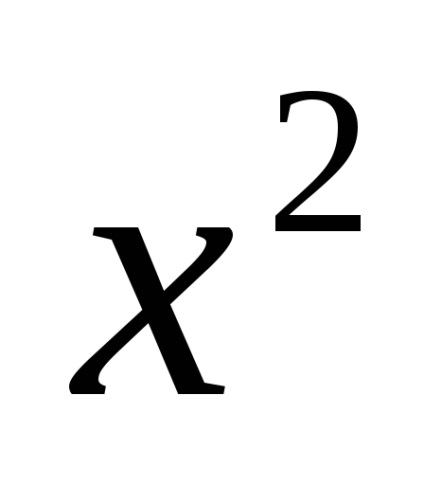
Akkor az egyenletben találtunk 2. gyökere feltételek

, ahol 2 - ismert gyökér, és 6 - szabad faktor (Wyeth-tétel).

.

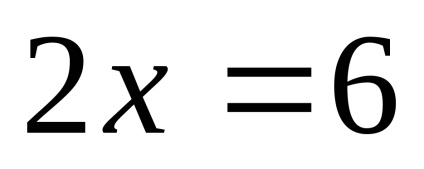
zárójel

kapunk a maradék talált 3. módszerrel.

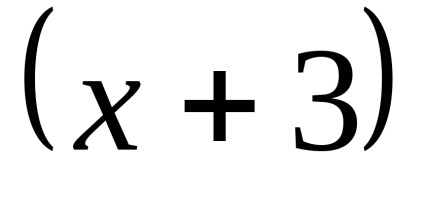
PR6. Nagyítás bizonytalanság

, bővülő frakció faktoring:

.

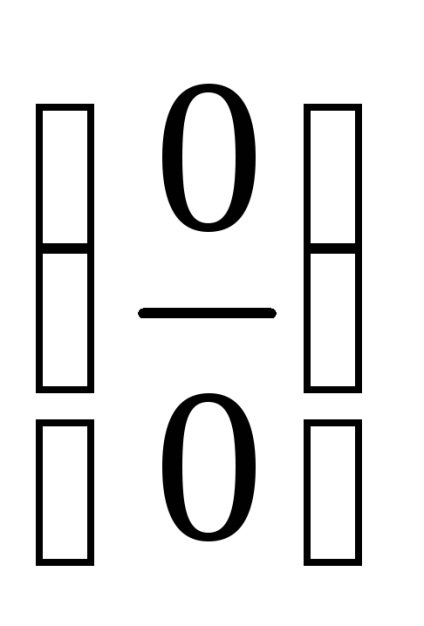
A határérték racionális függvény a végtelenben

Adott egy függvény

(Lásd. P. 16) és annak szükségességét, hogy. Kiderült, hogy amikoregész frakciót viselkedik az arány a magasabb hatásköre:

.

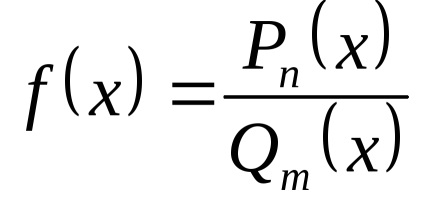
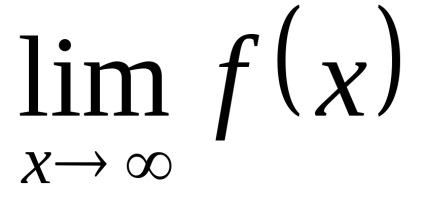
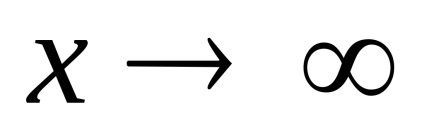
Aztán. jelent

. Jelenleg 3 esetekben:

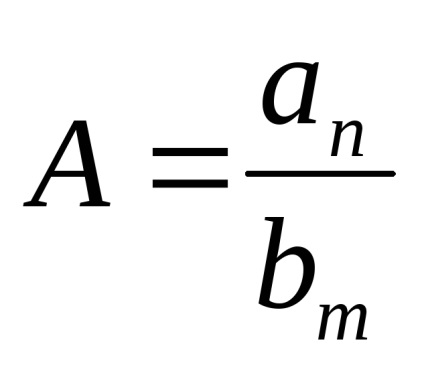
Így a határ

a) a végtelenhez, ha a mértéke a számláló nagyobb, mint a foka a nevező;

b) 0 egyébként;

c) ellen, a vezető együtthatók, ha a fok egyenlő.

PR7. megtalálják a határok

PR8. megtalálják a határok

11. példa elhagyva a számláló és a nevező a felsőbb hatalmak, azt látjuk,

12. példa A túl magas szinten, azt látjuk, hogy

Felhívjuk figyelmét, hogy a végtelen jele (ha kiderül) a válasz nem jelezték. Azonban, ha mind a felsőbb hatalmak - a páros (vagy ha mindkettő igaz), természetesen, a hozzáállás mindig pozitív, hogy lehet venni.

PR9. Keresse a korlátokat a funkciók

pontokon,,,,, valamint.

.

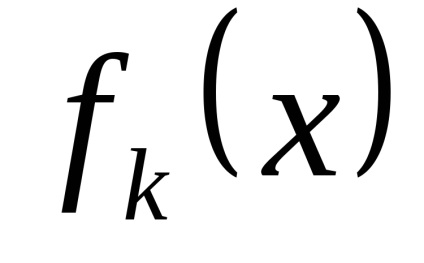
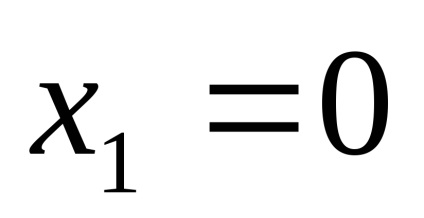
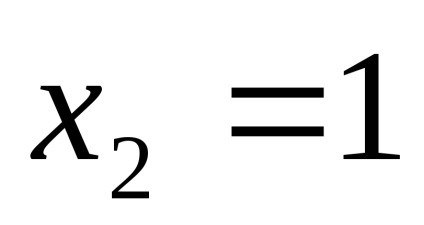
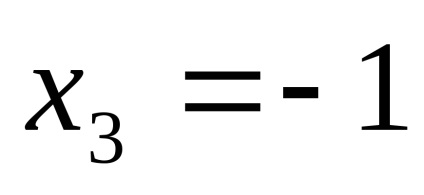
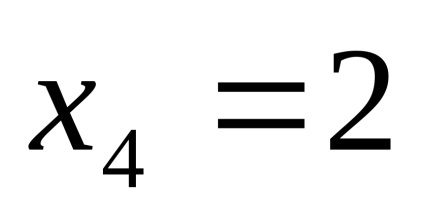
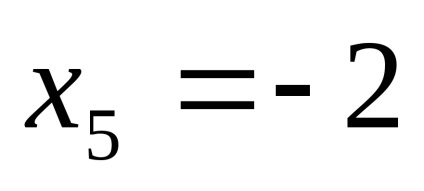
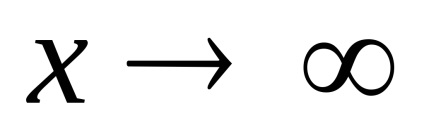
Korlátai irracionális függvények

Ha a függvény tartalmazza a gyökér, helyettesítő, mint mindig, a határpont. Kapcsolatos nehézségek a bizonytalanság

, ha kell szorozni a számláló és a nevező nasopryazhonnoe kifejezést.

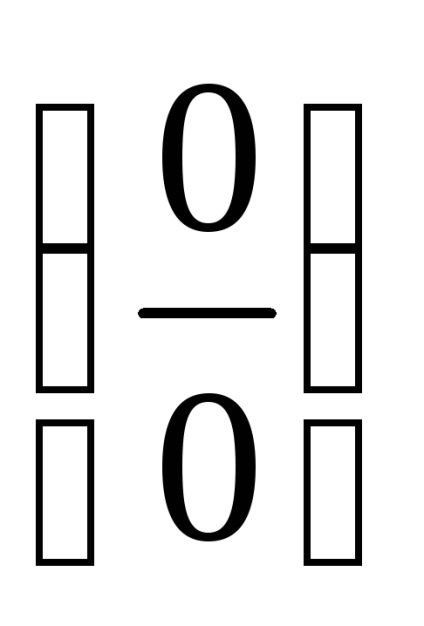
Kifejezések sopryazhenyotnositelno négyzetes eltéréseket. Ha a terméket alakítjuk négyzete közötti különbségének a képlet.

Példák a konjugátum expressziós

a)

összefüggő, ahol;

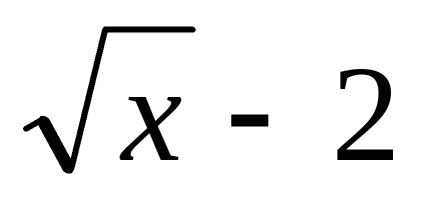
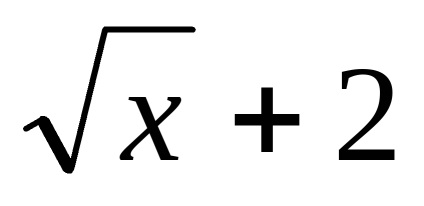
b)

összefüggő, majd;

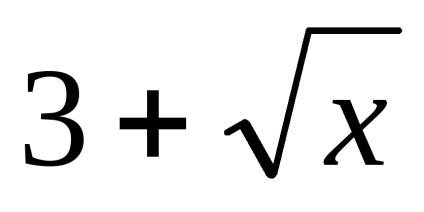
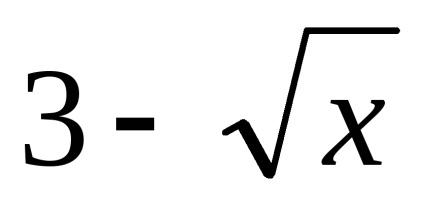
c)

összefüggő, mint

,

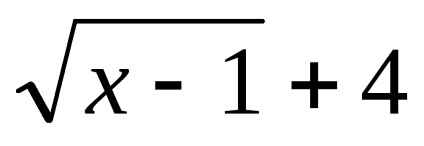
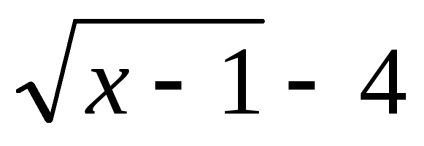
És a gyökere minden változatlan marad;

.

PR10. Keresse meg a határait irracionális funkciók egy egyszerű helyettesítés:

13. példa Behelyettesítve ezeket a pontokat, azt találjuk az értékeket

PR11. Nagyítás bizonytalanság

, megszorozzuk a számláló és a nevező egy alkalmas konjugátum kifejezés és csökkentett ugyanaz zárójelben:

.

.

.

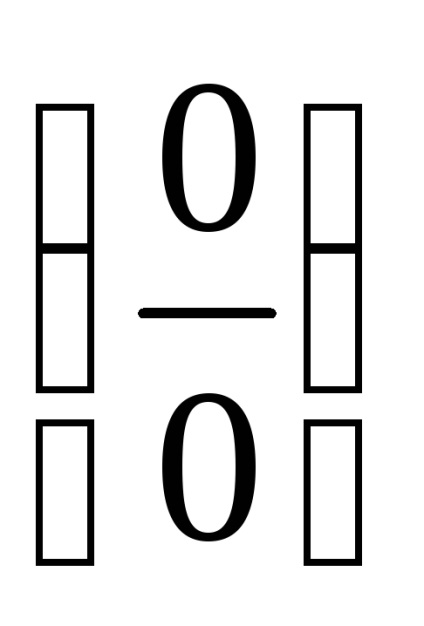
PR12. Szorozzuk meg a számláló és a nevező az expressziós, konjugátum a számlálót, majd - a kifejezés, konjugátum a nevező. Csökkentése konzolok, bővíteni a bizonytalanság

:

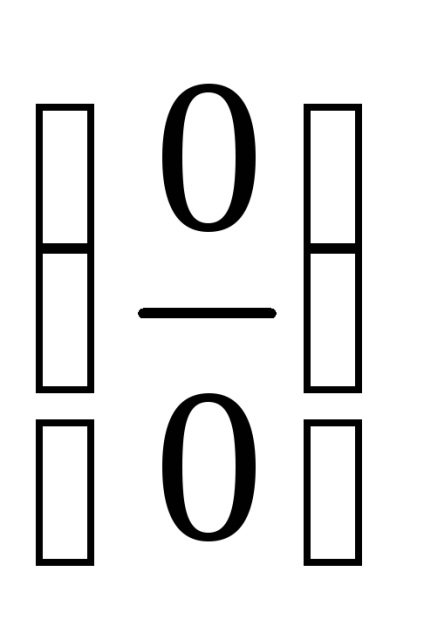
17. példa többszörösen szerezni a különbség négyzetek:

.

18. példa a 17. példa,

.

Irracionális határértékek

abban az esetben a bizonytalansághasonló racionális felhasználásával nagyobb teljesítményű, és kétség eseténCsökkentsdalkalmazásával konjugátum kifejezés.

Kapcsolódó cikkek

• Limit függvény a végtelenben - studopediya

• Mezőgazdasági Minisztérium fogja változtatni a nevét, és adjunk hozzá funkciókat, klub gabona piaci szakértők

• Hogyan javíthatnánk reproduktív funkciót férfi, női csapat