Interpoláció összeköti a pontokat úgy, hogy szép volt, savepearlharbor
Hogyan kell felhívni a grafikon n pontokat? A legegyszerűbb -, hogy megjelölje a markerek a hálóra. Az egyértelműség kedvéért azonban, akarnak csatlakozni egy könnyen olvasható sor. Csatlakoztassa a pontok legegyszerűbb egyenes szakaszok. De egy törött grafikus szól elég nehéz: meg kapaszkodik sarkok és nem csúszik a vonal mentén. És nézd törések nem túl szép. Kiderült, hogy amellett, hogy vonalláncok kell tudni építeni és görbék. Azonban óvatosnak kell lenni, hogy nem kap ez itt:
Egy kicsit felszerelések
Recovery közbenső függvény értékei, ami ebben az esetben táblázatos formában a P1 pontok # 038; nbsp ... # 038; nbspPn. Ez az úgynevezett interpolációs. Számos módja interpoláció, de lehet csökkenteni, ami szükséges, hogy megtalálják n # 038; nbsp- # 038; nbsp1 funkció kiszámításához a közbenső pontok az adott szegmenshez. Ebben alapérték kell lennie, megfelelő kiszámítható függvényt. Ennek alapján ütemtervet, és lehet építeni:
Funkciók fi nagyon eltérő lehet, de a leggyakrabban használt polinomok valamelyest. Ebben az esetben a végső interpoláló függvény (szakaszonként definiált időközönként pont által határolt Pi) egy spline.
kísérletezni
A legegyszerűbb példa - lineáris interpoláció, amely felhasználja polinomok az első fokú, de a végén kiderül, egy törött összekötő megadott pontokat.
Adjunk hozzá egy sajátosságait. Itt van egy ponthalmaz (már majdnem a mennyezet):
Az eredmény lineáris interpoláció e pontok a következők:
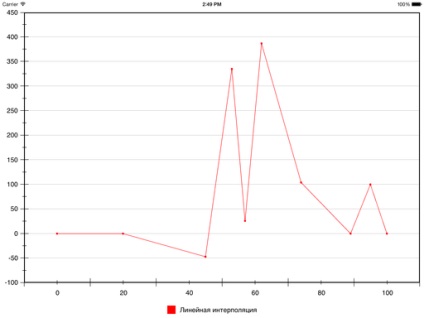
Azonban, mint már említettük, néha azt szeretnénk, hogy a végén egy sima görbe.
Mi sima? Fogyasztói válasz: nincs éles sarkok. Matematikai: folytonosság származékok. Ebben az esetben, a sima matematika megrendelés számával egyenlő az utolsó folyamatos származék, és a terület, ahol ez a folytonosság fenntartását. Azaz, ha a funkciót simaságát sorrendben 1 intervallumon [a; # 038; nbspb], ez azt jelenti, hogy [a; # 038; nbspb] van egy folytonos első származékot, de a második származék egy folytonossági hiány néhány pont.
Az összefüggésben a spline simaság a hiba fogalma. Hibák spline - a különbség közte és annak mértéke a simaság. A mértéke a spline - maximális felhasználása polinomok benne.
Fontos megjegyezni, hogy a „veszélyes” pont a spline (ami megzavarhatja a simaság) csak Pi. azaz, a csomópont szegmensek, amelyekben van egy átmenet az egyik a másikra polinom. Minden más szempontból a „biztonság”, mert a polinom saját domain definíció nincs gond a folytonosság származékok.
Ahhoz, hogy a sima interpoláció, akkor növelni kell a mértéke a polinomok és vegye fel azok aránya, hogy folytonosságának megőrzése a származékos a határ pont.
Hagyományosan, hogy megoldja ezt a problémát a harmadik fokú polinomok és elérni folytonosságát az első és a második deriváltak. Mi ez az úgynevezett harmadfokú spline hiba 1. Itt van, hogyan néz ki a mi adatok:
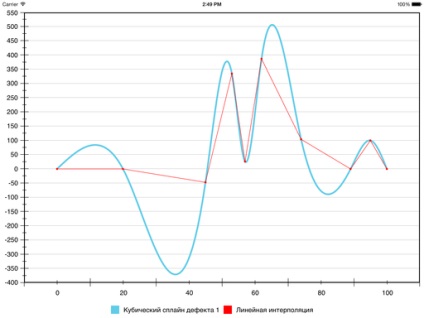
A görbe nagyon sima. De ha feltételezzük, hogy ez a grafikon egy folyamat vagy jelenség, amely bizonyítani kell, hogy az érintett személy, egy ilyen módszer valószínűleg nem megfelelő. A probléma a hamis szélsőségek. Úgy tűnt, mert a túl sok görbület, amelynek célja az volt, hogy biztosítsa a sima a interpolációs függvény. De a néző ilyen viselkedés nem az út, mert megtévesztette tekintetében a csúcsértékek a funkciót. És a kedvéért a vizuális képalkotás ezen értékek, sőt, mindent, és ez indult.
Tehát meg kell keresni más megoldásokat.
Egy másik hagyományos megoldás más, mint a köbös spline hiba 1 - Lagrange polinomok. Vannak polinomokként n # 038; nbsp- # 038; nbsp1 elfogadó alapértékek adott pontjain. Azaz, felosztás szegmensek nem ez a helyzet, a teljes szekvenciát által leírt polinom.
De itt van, mi történik:
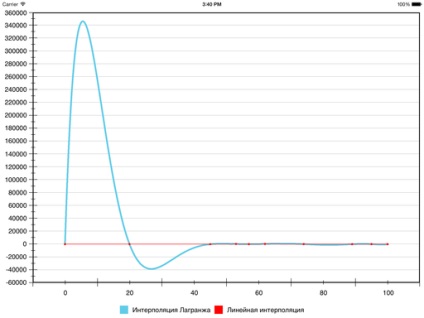
Simaság természetesen jelen van, de a látótávolság szenvedett annyira, hogy ... talán meg kell keresni más módszerekkel. Egyes adatsor az eredmény normális, de az általános esetben, a hiba tekintetében lineáris interpoláció (és így a hamis szélsőségek) állíthatók elő túl sok -, mert az a tény, hogy csak egy polinom minden szegmensben.
A számítógépes grafika, Bezier görbék igen széles körben használják. által képviselt polinomok k-ed-fokú.
Ezek nem interpolált, mert k # 038; nbsp + # 038; nbsp1 pontok részt vesznek az építőiparban, a kapott görbe áthalad csak az első és az utolsó. A fennmaradó K # 038; nbsp- # 038; nbsp1 pont szerepét egyfajta „gravitációs központ”, vonzza a görbe.
Itt látható egy példa a köbös Bezier görbe:
Hogyan lehet használni interpolációjához? Az ezek alapján görbék is lehet építeni egy spline. Azaz, az egyes spline szegmens lesz egy Bezier görbe K-ed-fokú (az úton, K # 038; nbsp = # 038; nbsp1 ad lineáris interpoláció). És a kérdés csak az, hogy mit k venni, és hogyan lehet megtalálni k # 038; nbsp- # 038; nbsp1 közbenső pont.
Végtelen sok választás (hiszen k nem korlátozott), de nézzük meg egy klasszikus: k # 038; nbsp = # 038; nbsp3.
A kapott görbe sima, szükséges, hogy elérjék a hiba 1 komponensei számára a spline, azaz a megőrzése a folytonosságát az első és a második deriváltak a pontokon csuklási szegmensek (Pi), ahogy az a klasszikus változata a köbös spline.
A megoldás erre a problémára részletesen (forráskód) tartják itt.
Ez az, ami történik a mi tesztsorozat:
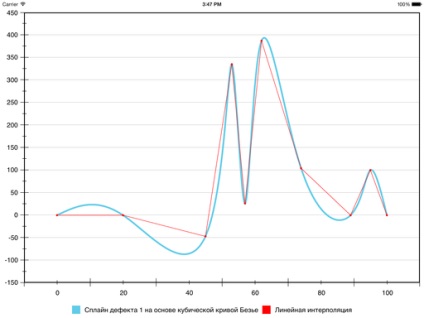
Ez még jobb lett: false szélsőségek még mindig ott van, de legalább nem olyan nagyon különbözik a valódi is.
Gondolunk és kísérletezés
Meg lehet próbálni, hogy gyengítse a simasága: szükség hiba 2, nem 1, azaz, hogy fenntartsák a folytonosságot az első derivált egyedül.
Egy elégséges feltétel eléréséhez a hiba 2 az a tény, hogy a közbenső ellenőrző pontok a köbös Bezier görbe szomszédos adott pontján az interpolált szekvenciák ettől a ponttól egy vonal, és egyenlő:
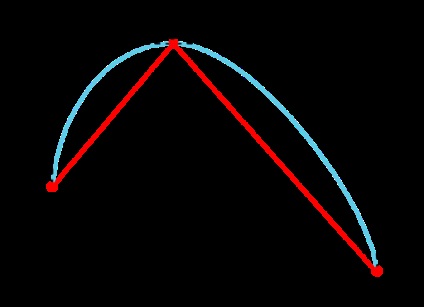
Mivel a vonalak, amelyek vannak olyan pontok Ci # 038; nbsp- # 038; nbsp1 (2). Pi és Ci (1). célszerű, hogy egy érintőleges A grafikon funkció interpolálandó a Pi pont. Ez biztosítja, hogy nem hamis szélsőérték a Bezier görbe meredek korlátozott épülő ellenőrzési pontok (ha a szaggatott vonal nem metszi önmagát).
Próbálgatással heurisztikus számítani a távolság az interpolált pont egy közbülső folyamatvezérlésénél kiderült az alábbiak szerint:

Az első és az utolsó ellenőrzési pontok köztes az első és utolsó pontja a grafikon, illetőleg (pontok C1 (1) és a Cn # 038; nbsp- # 038; nbsp1 (2) egybeesik a P1 pontok és Pn sorrendben).
Ebben az esetben kiderül, hogy egy görbe:
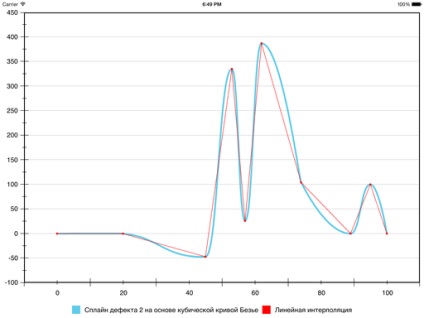
Mint látható, a hamis szélsőértékek többé. Ugyanakkor, ha összehasonlítjuk a lineáris interpoláció, néha nagyon nagy hiba. Akkor lehet, hogy még kevésbé, de aztán viszont fogják használni még trükkösebb heurisztikus.
A jelenlegi verzió jöttünk, csökkentve a sima egy nagyságrenddel. Meg tudod csinálni még egyszer: hagyja, hogy a spline lesz hiba 3. Tény, hogy a legtöbb hivatalos funkció nem lesz sima egyáltalán: még az első származék lehet folytonossági. De ha szakad el figyelmesen, vizuálisan semmi rossz nem fog történni.
Mi elhagyni a követelményt, hogy a távolság a lényeg Pi pont Ci # 038; nbsp- # 038; nbsp1 (2) és a Ci (1). de mi tartja őket mind egy sorban:
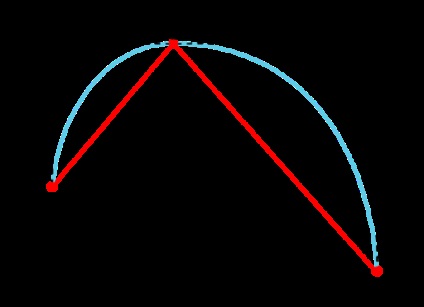
A heurisztika kiszámításához távolságok lesznek:
Számítása L1 és L2 jelentése ugyanaz, mint a „heurisztikus 1”.
Ugyanakkor azonban többet ér, hogy ellenőrizze, nem ért egyet, hogy a pont Pi és Pi # 038; nbsp + # 038; nbsp1 ordináta, és ha a mérkőzés, hisz l1 # 038; nbsp = # 038; nbspl2 # 038; nbsp = # 038; nbsp0. Ez véd „duzzanat” grafikus sík szakaszok (ami szintén fontos a valóságnak adatokat a kijelzőt).
Az eredmény a következő:
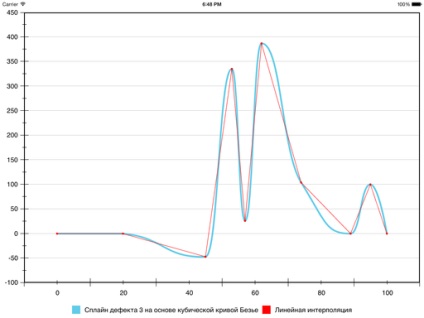
Ennek eredményeként a hiba a hatodik szegmens csökkent, de a hetedik - fokozott: a görbületi Beziers rajta több volt, mint szeretnénk. Orvosolja a helyzetet lehet erőszakkal görbületének csökkentésének, és így „nyomott” Bezier közelebb a vonalszakaszt, amely összeköti a határvonal szegmensben. Ehhez használja a következő heurisztikus:
Ha abszcisszájának metszéspontja húzható érintők Pi pont (xi, # 038; nbspyi) és Pi # 038; nbsp + # 038; nbsp1 (xi # 038; nbsp + # 038; nbsp1, # 038; nbspyi # 038; nbsp + # 038; nbsp1) fekszik, az [xi; # 038; nbspxi # 038; nbsp + # 038; nbsp1], akkor L1 vagy L2 zérus. Abban az esetben, ha az érintő pontban Pi pedig felfelé nulla feltételezik legfeljebb L1 és L2. Ha le - minimum.
Ezzel szemben úgy döntött, hogy befogadja a cél eléréséig.
Lehet, hogy valaki jól jön kódot.
Amit az emberek csinálnak valamit?
Az ígért felülvizsgálata. Természetesen, mielőtt a probléma megoldása néztük, aki tud felmutatni, és csak ezután kezdte megérteni, hogyan teszik magukat, és esetleg jobb. De itt egyszer már megtörtént, nem öröm nélkül, ismét átvágott a rendelkezésre álló eszközök és eredményeiket összevetettük a kísérleteink eredményeit. Tehát ott megy.
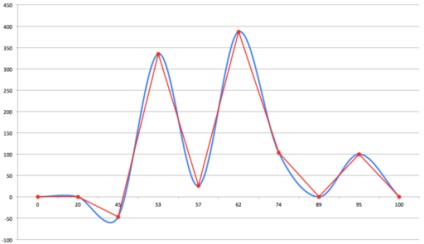
Ez nagyon hasonló a spline a hiba 1, alapul a Bezier görbéket a fentiekben tárgyaltuk. Azonban, ellentétben ez a tiszta formában, már csak két hamis szélsőérték - az első és a második szegmens (mi volt négy). Úgy tűnik, a klasszikus megállapítása közbenső ellenőrző pontok, majd hozzáadunk néhány heurisztikus. De minden hamis szélsőérték azok nem kerülnek mentésre.
LibreOffice Calc
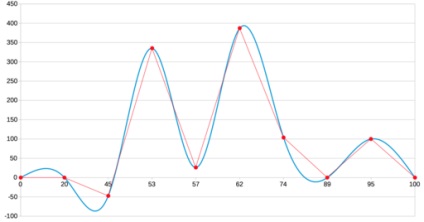
A beállítások az úgynevezett harmadfokú spline. Nyilvánvaló, hogy ez is alapul Bezier, és itt már van egy másolata az eredményeink: négy hamis szélsőérték helyén.
Van még egy fajta interpolációs, amelyhez nem tartozik ide: B-spline. De ez nyilvánvalóan nem alkalmas a probléma, mert itt ad ez az eredmény 🙂
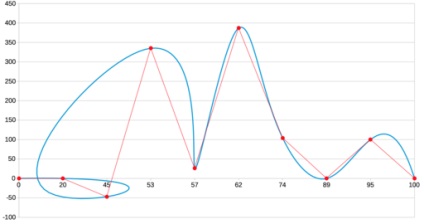
Highcharts. Az egyik legnépszerűbb JS-könyvtárak ábrázolási
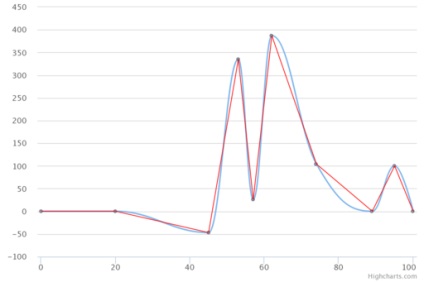
Itt van egy „tangens módszer” a kiviteli alaknál azonos távolságra a interpolált pont a közbenső ellenőrző szekvencia. Hamis szélsőértékből nem, de van egy viszonylag nagy hibát képest lineáris interpolációval (hétszegmenses).
amCharts. Egy másik népszerű JS-könyvtár
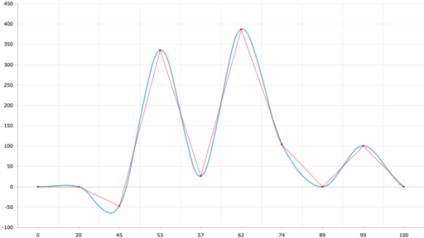
A kép nagyon hasonlít ekselevskuyu, ugyanazt a két szélsőérték hamis ugyanazon a helyen.
Coreplot. A legnépszerűbb ábrázolási könyvtár iOS és OS X
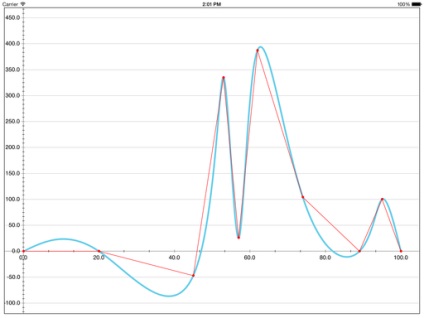
Vannak hamis szélsőségek, és egyértelmű, hogy a használata a spline hiba 1 alapján Beziers.
A könyvtár nyitva van, így láthatja a kódot, és látni ezt.
aChartEngine. mint például a legnépszerűbb ábrázolási könyvtár Androidra
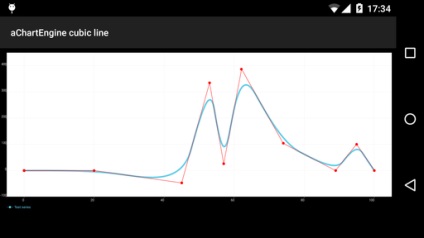
A legtöbb hasonló a Bezier görbe fokú N # 038; nbsp- # 038; nbsp1, bár a legtöbb grafikus könyvtár úgynevezett «köbös vonal». Furcsa! Bárhogy legyen is a helyzet, ott nem csak jelen hamis szélsőségek, de elvileg nem teljesülnek feltételeket interpoláció.
ahelyett, hogy a következtetés
A végén kiderül, hogy a „nagy fiúk” legjobb probléma megoldódott Highcharts. De a leírt módszer ebben a cikkben, hogy több kisebb hiba viszonyított lineáris interpoláció.
Általában ezt kellett kérésére az ügyfelek, akik zareportili bennünket „éles sarkok”, mint egy hiba a motor listákon. Mi lesz boldog, ha a leírt kísérlet hasznos valakinek.